8. Дифференцирование обратных тригонометрических функций

228

Замечание. Производные функций arcsin u и arccosu отличаются только знаком.

349—352. Найти производные следующих функций:

229

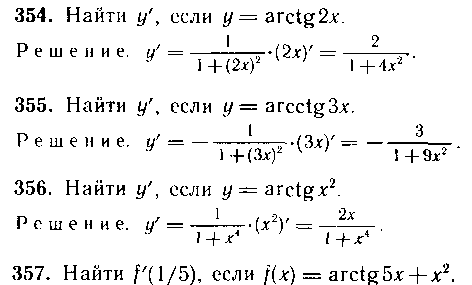
Решение. Имеем

Следовательно,

358. Дано: Решение.

230

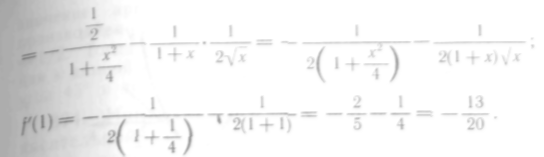
3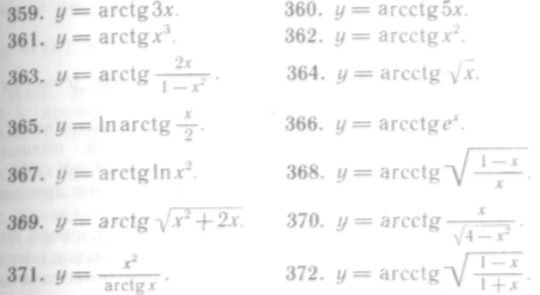 59372. Найти производные следующих функций:

§ 5. Геометрический и механический смысл производной

• 1. Геометрический смысл производной

• 2. Механический смысл производной

• 3. Производная второго порядка и ее механический смысл

• 4. Приложения производной к решению физических задач

1. Геометрический смысл производной

Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, состоит в следующем: значение производной функции в точке х равно угловому коэффициенту касательной, проведенной к графику функции в той же точке х (см. рис. 99), т. е.

Таким образом, если функция в точке х имеет производную, то график этой функции в точке с абсциссой х имеет касательную, и, наоборот, если в некоторой точке с абсциссой х существует касательная к графику, то при этом значении х существует производная. Иначе говоря, существование касательной к кривой в некоторой точке с абсциссой х необходи-

231

Уравнение нормали запишется в виде

232

Учитывая это рассмотрим каждое из условий задачи.

233

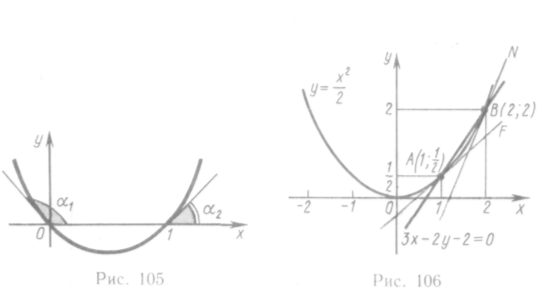
377. Найти углы, под которыми парабола пересекает ось абсцисс (рис. 105).

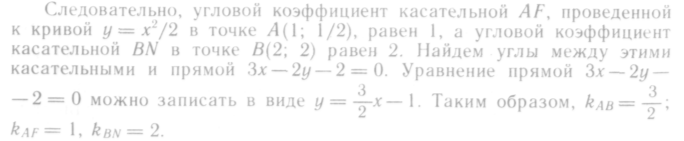
Из аналитической геометрии известна формула для нахождения тангенса угла между двумя прямыми по заданным угловым коэффици­ентам этих прямых:

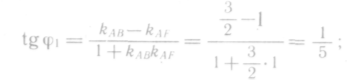
234

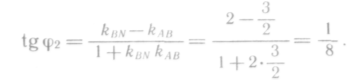
Так как нормаль и касательная, проведенные в одной точке кривой, взаимно перпендикулярны, то угловой коэффициент нормали _. Подставляя полученные значения k₁ и k₂ в уравнение пучка прямых, найдем искомые уравнения касательной и нормали:

235

Решение. Угловой коэффициент данной прямой . Угловой коэффициент касательной .

Из условия параллельности следует . Тогда ; . Следовательно, — абсцисса точки касания. Подставляя это значение х в уравнение кривой, получим орди­нату точки касания:

Итак, в точке (3; 10) касательная к данной кривой параллельна прямой .

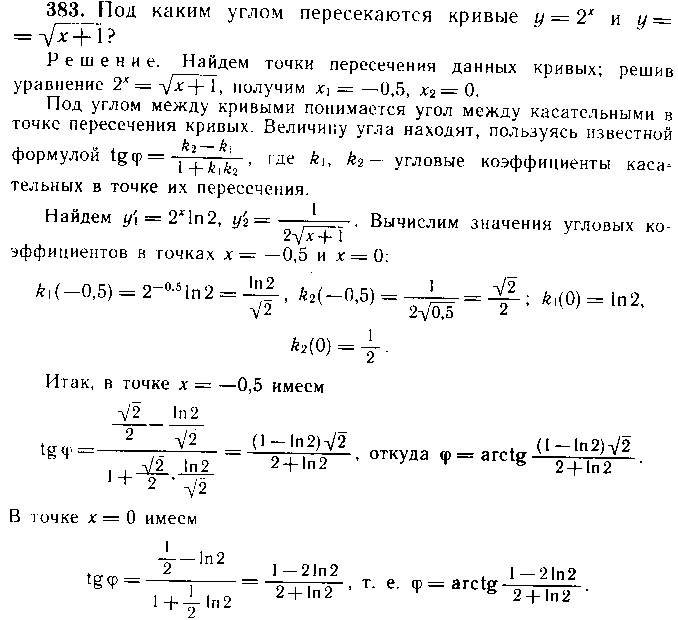
384.В какой точке касательная к кривой образует с осью угол 30°?

385. Найти абсциссу точки параболы , в ко­ торой касательная параллельна оси абсцисс.

236

2. Механический смысл производной

Механическое истолкование производной было впервые дано И. Ньютоном. Оно заключается в следующем: скорость движе­ния материальной точки в данный момент времени равна произ­водной пути по времени, т. е.

Таким образом, если закон движения материальной точки задан уравнением , то для нахождения мгновенной скорости точки в какой-нибудь определенный момент времени нужно найти производную и подставить в нее соответствующее значение t. Для определенности будем считать, что путь измеряется в метрах, а время — в секундах.

237

405. Путь, пройденный материальной точкой, задается следующей функцией времени: .

Найти скорость движения точки в конце 5-й секунды.

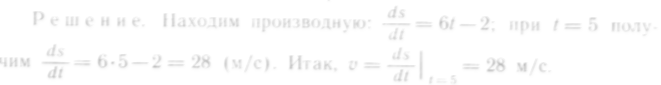
406. Точка движется прямолинейно по закону _.Найти ее скорость в момент времени _.

407. Найти скорость движения материальной точки в конце 3-й секунды, если движение точки задано уравнением

.

408. Точка движется прямолинейно по закону _. В какой момент се скорость окажется раиной нулю?

409.Дна тела движутся прямолинейно: одно по закону

, другое - по закону . Определить мо­мент, когда скорости этих тел окажутся равными.

410. Высота тела, брошенного вертикально вверх, меняется в зависимости от времени по закону . Найти скорость тела в конце 10-й секунды. Сколько секунд тело будет лететь вверх и какой наибольшей высоты оно достигнет?

Подставляя это значение в уравнение движения, получим наибольшую высоту, на которую поднимается тело:

411. Для машины, движущейся со скоростью 30 м/с, тормоз­ной путь определяется формулой — путь в метрах, t время торможения в секундах. В течение какого времени осуществляется торможение до полной остановки машины? Какое расстояние пройдет машина с начала торможе­ния до полной ее остановки

412. Зенитный снаряд выброшен вертикально вверх с началь­ной скоростью v₀. Через сколько секунд снаряд достигнет наивыс­шей точки?

413.Тело массой 8 кг движется прямолинейно по закону . Найти кинетическую энергию тела через 3 с после начала движения.

Решение. Найдем скорость движении тела в любой момент вре­мени t:

238

Вычислим скорость тела в момент времени t = 3:

Определим кинетическую энергию тела и момент времени t = 3:

414. Найти кинетическую энергию тела через 4 с после начала движения, если его масса равна 25 кг, а закон движения имеет вид .