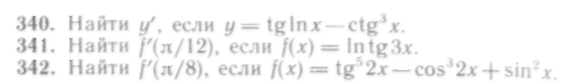- •Глава IV
- •§ 1. Свойства и графики основных элементарных функций
- •1. Постоянные и переменные величины
- •2. Область изменения переменной
- •3. Определение функции. Частное значение функции
- •4. Область определения функции
- •5. Способы задания функции
- •6. Основные свойства функций
- •7. Основные элементарные функции
- •§ 2. Предел и непрерывность функции
- •1. Предел переменной величины
- •2. Основные свойства пределов
- •3. Предел функции в точке
- •4. Приращение аргумента и приращение функции
- •5. Понятие о непрерывности функции
- •8. Вычисление пределов
- •§ 3. Производная
- •1. Задачи, приводящие к понятию производной
- •2. Определение производной
- •3. Общее правило нахождения производной
- •4. Частное значение производной
- •5. Связь между непрерывностью и дифференцируемостью функции
- •§ 4. Правила и формулы дифференцирования элементарных функций
- •1. Таблица правил и формул дифференцирования
- •2. Правила дифференцирования алгебраической суммы, произведения и частного
- •3 Правило дифференцирования сложной функции
- •4. Дифференцирование логарифмических функций
- •5. Производная степенной функции
- •6. Производная показательной функции
- •7. Дифференцирование тригонометрических функций
- •327. Найти
- •8. Дифференцирование обратных тригонометрических функций
- •358. Дано: Решение.
- •§ 5. Геометрический и механический смысл производной
- •1. Геометрический смысл производной
- •2. Механический смысл производной
- •3. Производная второго порядка и ее механический
- •4. Приложения производной к решению физических задач
- •§6. Дифференциал
- •1. Понятие дифференциала
- •2. Геометрический смысл дифференциала
- •3. Вычисление дифференциала
- •4. Дифференциал сложной функции
- •5. Применение дифференциала в приближенных вычислениях
- •§ 7. Исследование функций и построение графиков
- •1. Возрастание и убывание функций
- •2. Исследование функции на экстремум с помощью первой производной
- •3. Исследование функции на экстремум с помощью второй производной
- •4. Наибольшее и наименьшее значения функции
- •5. Практическое применение производной
- •6. Вогнутость и выпуклость. Точки перегиба
- •7. Построение графиков функций
5. Производная степенной функции
Найдем производную
функции![]() ,
где п —
любое действительное число. Для этого
применим способ, который называется
логарифмическим
дифференцированием. Он
заключается в том, что функцию сначала
логарифмируют, а затем находят
производную.
,
где п —
любое действительное число. Для этого
применим способ, который называется
логарифмическим
дифференцированием. Он
заключается в том, что функцию сначала
логарифмируют, а затем находят
производную.
Прологарифмируем
функцию
![]() по основанию
е:
по основанию
е:
![]()
Дифференцируя обе части этого равенства, имеем
![]()
Левую часть
последнего равенства можно записать
в виде
![]() (так как у
— сложная
функция от х),
а правую
часть - в виде
(так как у
— сложная
функция от х),
а правую
часть - в виде
![]() .
Поэтому
.
Поэтому
![]() ,
т. е.
,
т. е.
![]()
![]() . Но
. Но
![]() и,
следовательно,
и,
следовательно,
![]()
откуда
![]()
Мы получили обобщение известной формулы производной степени, справедливое для любого показателя.
Найдем производную
функции
![]() где
где![]() .
Восполь- зовавшись правилом
дифференцирования сложной функции,
получим
.
Восполь- зовавшись правилом
дифференцирования сложной функции,
получим
![]() .
Итак,
.
Итак,
![]()
279—300. Найти производные следующих функций:
279.![]()
220

Решение. Применяем правило дифференцирования частного и формулу X:
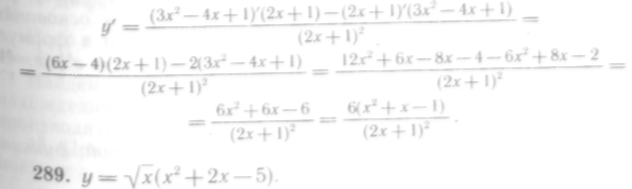
221
Решение. Здесь следует воспользоваться правилом дифференцирования произведения и формулой X. Имеем

6. Производная показательной функции
Производную показательной функции также можно найти с помощью логарифмического дифференцирования.
Пусть дана функция
![]() ,
где a>0
и
,
где a>0
и
![]() .
Логарифмируя
.
Логарифмируя
обе части равенства
по основанию е,
получим
![]() .
Про-
.
Про-
дифференцируем обе части равенства:
![]()
Откуда
![]() или
или
![]() .
Следовательно,
.
Следовательно,
![]()
Итак, производная
показательной функции
![]() равна
W
равна
W
изведению этой функции на натуральный логарифм основан
Найдем производную
функции
![]() .
Для этого в формуле
.
Для этого в формуле
![]() положим
а=е; тогда
получим
положим
а=е; тогда
получим
![]()
![]() и, следовательно,
и, следовательно,
![]()
Итак, производная
функции
![]() равна
самой функции
равна
самой функции
![]()
222
Производные
функций
![]() найдем,
применив формулу хождения производной
сложной функции. В результате
найдем,
применив формулу хождения производной
сложной функции. В результате
![]()
производная
функции
![]() ,
где
,
где
![]() ,
равна самой функции умноженной на
натуральный логарифм основания и на
производную промежуточного аргумента
и.
,
равна самой функции умноженной на
натуральный логарифм основания и на
производную промежуточного аргумента
и.
Производная
функции
![]() ,
где
,
где
![]() ,
равна
произведе-
,
равна
произведе-
самой функции еu на производную промежуточного аргу-

7. Дифференцирование тригонометрических функций
Производные
функций
![]() ,
где
,
где
![]()
Найдем производную
функции
![]() по общему
правилу прохождения
производной. Отметим, что функция
по общему
правилу прохождения
производной. Отметим, что функция
![]() имеет
производную при любом значении аргумента
х.
имеет
производную при любом значении аргумента
х.
10
Придадим аргументу х
приращение
![]() ;
тогда функция
;
тогда функция
получит
приращение
![]() :
:
223
![]()
2°.
Вычитая из нового значения функции
первоначальное, найдем
значение приращения![]() :
:
![]()
Применим формулу разности синусов:
![]()
Тогда получим
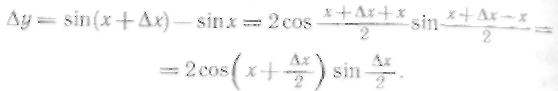
3°. Находим

4°. Перейдем к пределу:
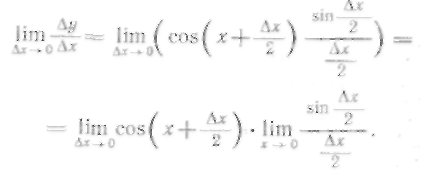
Если
![]() .
Поэтому, полагая
.
Поэтому, полагая
![]() ,
получим
,
получим
![]()
Но
![]() ,
так как функция
,
так как функция
![]() непрерывна.
непрерывна.
а
![]() (первый
замечательный предел). Значит,
(первый
замечательный предел). Значит,
![]()
![]() , т. е.
, т. е.
![]()
Итак, производная
функции
![]() равна
равна
![]()
Выведем
формулу дифференцирования функции
![]() ,
где
и —
функция от х.
Применяя
формулу
,
где
и —
функция от х.
Применяя
формулу
![]() находим
находим
224
![]()
Итак,![]()
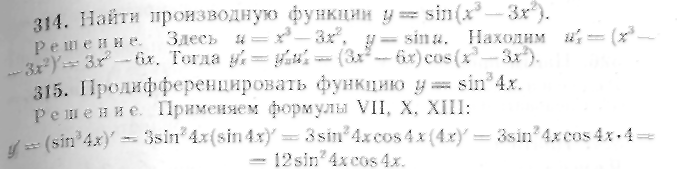
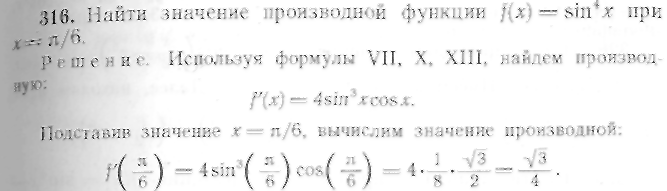
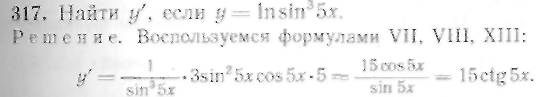
318—323. Найти производные следующих функций:
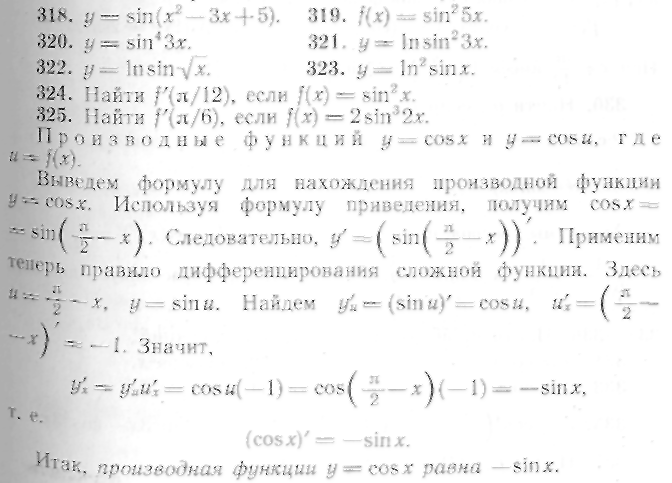
225
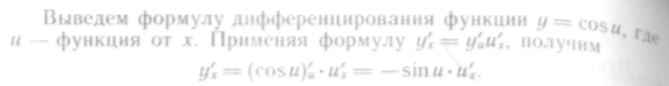
Итак,
![]()
326. Найти
производную функции
![]()
![]()
327. Найти
![]()
328. Найти производную
функции
![]()
![]()
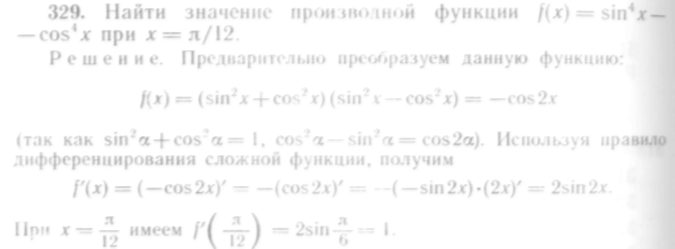
330. Найти у',
если
![]()

331—336. Найти производные следующих функций:
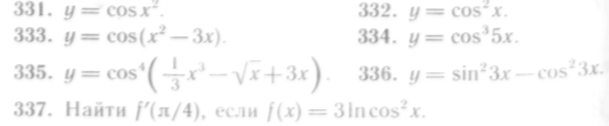
226

Следовательно,
![]()
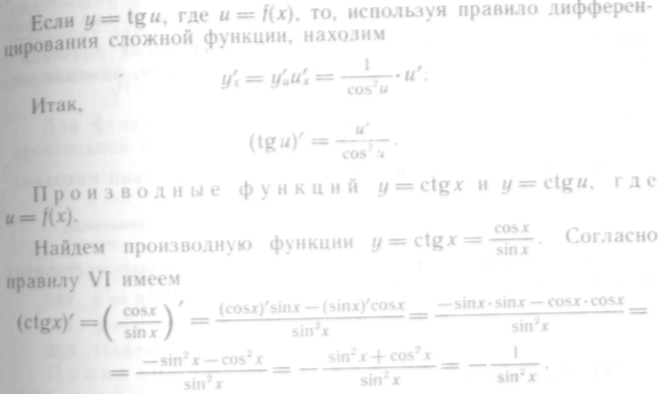
Значит,
![]()
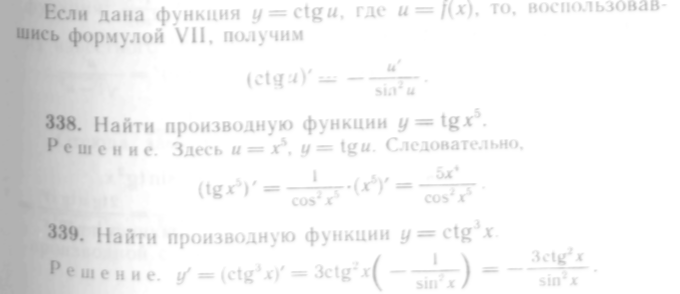
8* 227