3 Правило дифференцирования сложной функции

Поскольку стремится к нулю, в силу непрерывности функции приращение также стремится к нулю. Тогда получим

т.е производная функции у по аргументу х равна производной этой функции по промежуточному аргументу и, умноженной на производную промежуточного аргументам по основному аргумен­ту х.

215

коэффициент сложности, указывающий количество простых функций, входящих в данную сложную функцию. Он обозначается цифрой в кружке после записи функции. Например, для функции коэффициент сложности равен 2, так как в нее входят две простые функции _. Для функции y=sin²3x коэффициент сложности равен 3 (простыми функциями, составляющими данную, являются , ).

Очень важно правильно определить порядок следования про - межуточных функций. Например, для функции имеющей коэффициент сложности 4, промежуточные функции расположены в следующем порядке: 1) логарифмическая ; 2) степенная ; 3) тригонометрическая tg (3*)

4) линейная Зх.

238. Продифференцировать функцию

Решение. Коэффициент сложности данной функции равен 2. Со­ставляющими функции являются . Согласно правилу дифференцирования сложной функции, находим

239.Учитывая, что, продифференцировать функ­цию

Решение. Коэффициент сложности данной функции равен 2. По­рядок следования промежуточных функций таков: Находим

240. Найти , если

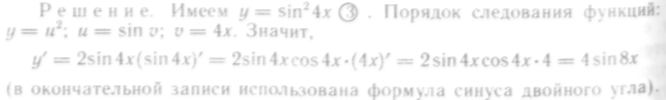
В дальнейшем, когда в практике дифференцирования накопит­ся достаточный опыт, можно обходиться без промежуточных запи­сей.

241—246. Найти производные следующих функций:

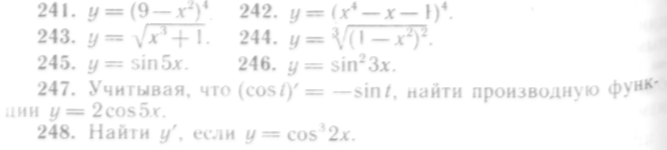
216

4. Дифференцирование логарифмических функций

Правую часть этого равенства умножим и разделим на х:

(это можно сделать, так как ).

Используя свойство логарифмов , можно за - писать

217

рифму предела функции, так как логарифмическая функция прерывна. Следовательно,

Учитывая, что , находим

Итак, производная функции равна единице, деленной

на аргумент.

Выведем формулу дифференцирования функции где

Используя формулу дифференцирования сложной функции , получаем , т. е.

Производная функции равна дроби, знаменателем

которой является промежуточный аргумент, а числителем — его производная по независимой переменной х.

249—260. Найти производные следующих функций:

249.

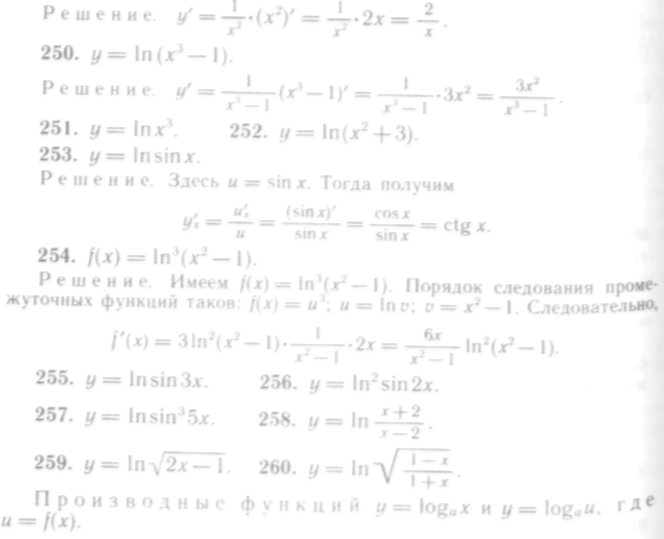
218

Если дан десятичный логарифм или логарифм числа по любому другому основанию, то следует воспользоваться формулой перехода от одной системы логарифмов к другой.

"Известно, что

Если положить , то логарифм числа по основанию а можно выразить через натуральный логарифм, а именно:

Воспользуемся последней формулой для нахождения произ­водной функции _. Имеем

Таким образом, производная функции равна еди-

нице, деленной на произведение аргумента и натурального лога­рифма основания.

Пусть теперь , где . Тогда согласно правилу

дифференцирования сложной функции имеем . Но и, следовательно,

261—278. Найти производные следующих функций:

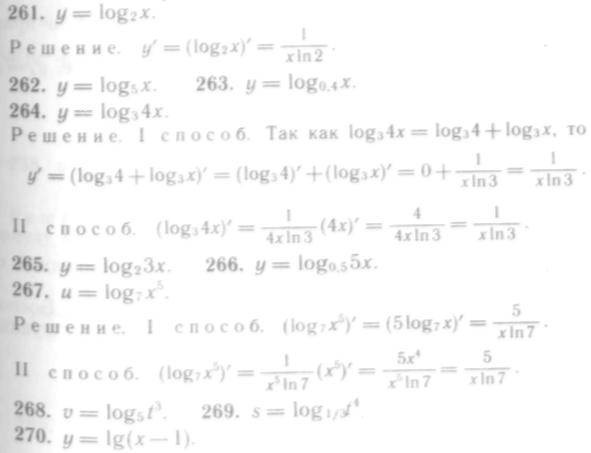
219