§ 4. Правила и формулы дифференцирования элементарных функций

• 1. Таблица правил и формул дифференцирования

• 2. Правила дифференцирования алгебраической суммы, произведения и частного

• 3. Правило дифференцирования сложной функции

• 4. Дифференцирование логарифмических функций

• 5. Производная степенной функции

• 6. Производная показательной функции

• 7. Дифференцирование тригонометрических функции

• 8. Дифференцирование обратных тригонометрических функций

1. Таблица правил и формул дифференцирования

О пределение производной по формуле четко указывает действия, которые нужно выполнить для ее на­хождения, что позволяет непосредственно вычислять производ­ную любой элементарной функции. Необходимо хорошо овладеть непосредственным дифференцированием, поскольку оно позволя­ет вывести основные правила и формулы дифференцирования. Эти правила и формулы следует обязательно знать, чтобы не повторять каждый раз все выкладки при нахождении данной функции. Ведь существует бесконечное множество функций и с их услож­нением непосредственное дифференцирование становится все более трудоемким.

Поэтому целесообразно вывести формулы производных. Для основных элементарных функций (степенной, показательной, логарифмической, тригонометрических и обратных тригономет­рических) и сформулировать правила дифференцирования суммы, разности, произведения и частного функций, а также правило диф ференцирования сложной функции, т. е. функции от функции.

208

Это позволит находить производные всех элементарных функций которые могут быть получены из основных элементарных функций и постоянных с помощью конечного числа арифметических действий и конечного числа операций взятия функции от функции.

Прежде чем доказывать правила и формулы дифференцирования. сведем их в таблицу и в дальнейшем будем пользоваться ею, подобно тому как в арифметике пользуются таблицей умно­жения.

209

2. Правила дифференцирования алгебраической суммы, произведения и частного

Производная постоянной. Пусть дана постоянна функция у = С. Тогда ее приращение . Следовательно, , т. е.

Итак, производная постоянной равна нулю. Например,

Производная независимой переменной Пусть дана функция у = х. Найдем ее производную по общему правилу.

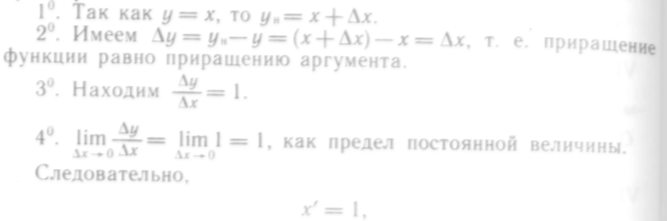
т. е. производная функции у = х равна единице.

Производная алгебраической суммы. Пусть дана функция , которую можно представить в виде алгебраической суммы слагаемых и, a, w, имеющих производную в точке х, т. е. . Найдем производную у' по общему

правилу.

Очевидно, что полученную формулу можно обобщить и любое число слагаемых: производная алгебраической суммы

210

Итак, производная произведения двух функций равна произ­водной первого сомножителя, умноженной на второй, плюс производная второго сомножителя, умноженная на первый.

Следствие. Постоянный множитель можно вынести за знак_ производной.

211

Производная степени равна произведению показателя степени на то же основание с показателем на единицу меньше.

В дальнейшем эта формула будет доказана для любого дей­ ствительного показателя.

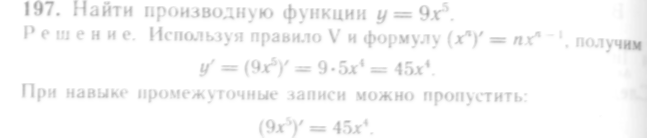
198. Найти производную функции

Решение. В правой части имеем алгебраическую сумму дифферен­цируемых функций, поэтому применяем правило III:

Используя результаты примеров 194 и 191. получим

200—214. Найти производные следующих функций:

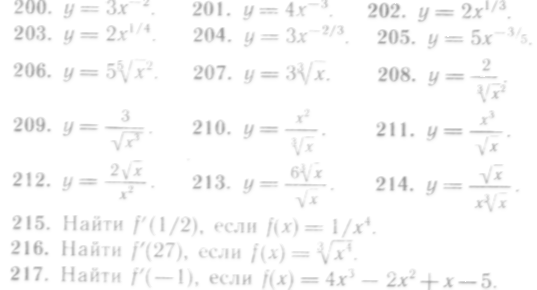
212

222—227. Найти производные следующих функций:

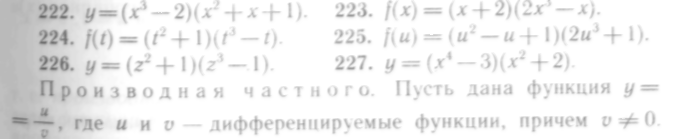
Следуя общему правилу нахождения производной, находим:

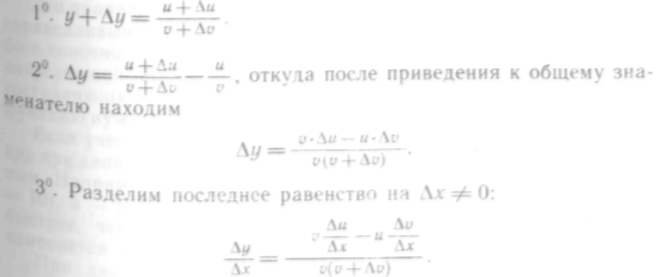
213

Итак, производная дроби равна дроби, знаменатель которой равен квадрату знаменателя данной дроби, а числитель равен производной числителя данной дроби, умноженный на ее знамена­тель, минус производная знаменателя, умноженная на числитель

230—237. Найти производные следующих функций:

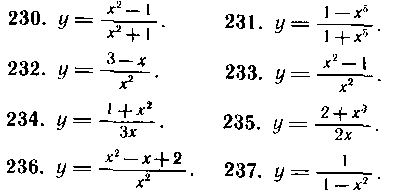
214