5. Парабола и ее уравнение

Параболой называется множество точек на плоскости, Равно- удаленных от заданной точки (называемой фокусом) и данной прямой (называемой директрисой).

Фокус параболы принято обозначать буквой F, директрису буквой d, расстояние от фокуса до директрисы — буквой

. Рассмотрим основные случаи расположения параболы

относительно осей координат.

158

Каноническое уравнение параболы, фокус которой расположен на оси абсцисс, (рис. 61, 62), имеет вид

Эти два случая представлены в следующей таблице:

142. Найти координаты фокуса и уравнение директрисы параболы заданной уравнением .

159

143. Найти каноническое уравнение параболы и уравнение J директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0; —3).

1.44. Составить уравнение параболы, имеющей вершину _{в н} чале координат, симметричной оси Ох и проходящей через точку J ЛОЗ; -6).

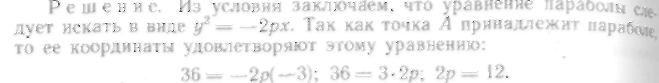
Итак, уравнение параболы имеет вид

145. Найти каноническое уравнение параболы и уравнение директрисы, если фокус параболы — точка г(—2; 0).

146. Парабола задана уравнением . Найти коорди­- наты ее фокуса и уравнение директрисы.

147. Парабола с вершиной в начале координат симметрична оси Оу и проходит через точку А(—5; 2). Составить каноническое уравнение параболы.

148. Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением

149. Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением

150. Составить уравнение параболы с вершиной в начале координат, если уравнение ее директрисы

151. Составить уравнение параболы с вершиной в начале координат, если уравнение ее директрисы

Вопросы и задачи для конспектирования

160

^{6-1356 161}

Ответы

Контрольное задание

Вариант 1

Вариант 2

162

Ответы

6*