3. Общее уравнение прямой

Прямые - самые простые линии на плоскости. Им соответ-

ветствуют и самые простые уравнения - уравнения первой степени.

Справедливо следующее утверждение: всякая прямая на

носкости определяется уравнением первой степени с двумя пе-

ременными х и y и обратно, всякое уравнение вида

при любых действительных значениях коэффициентов ,В, С, кроме случая одновременного равенства нулю коэффи­циентов А и В, определяет прямую.

Уравнение называется общим уравнением

прямой. Коэффициенты А, В, С принято записывать в виде

143

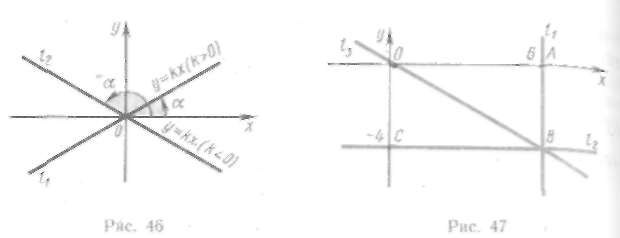
Напомним, что угловым коэффициентом называется тангенс угла наклона прямой к положительному направлению оси абс­цисс:

Если угол наклони острый, то угловой коэффициент если же угол наклона тупой, то угловой коэффициент (рис. 46).

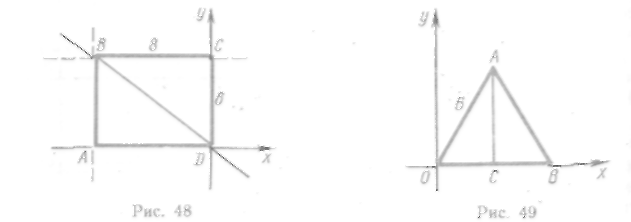
77. Составить уравнения прямых, изображенных на рис. 47.

4. Правило составления уравнения прямой

Положение прямой на плоскости относительно системы коор­динат можно задать различными способами. Прямая может быть, задана точкой и. направлением; точкой и перпендикулярным пря-

144

мой вектором; двумя точками; отрезками, которые прямая отсе­ет на осях координат (частный случай задания прямой двум точками).

Мы видим, что во всех случаях задания прямой обязательно должна быть известна хотя бы одна точка, через которую проходит искомая прямая. Кроме того, должно быть задано какое-либо дополнительное условие: коллинеарность, перпендикуляр­ность или вторая точка, принадлежащая прямой.

Правило составления уравнения прямой, для которой из­вестны координаты точки и задано какое-либо второе условие, состоит в следующем:

5. Уравнение прямой, проходящей через данную точку и. Имеющей заданный нормальный вектор

Нормальным вектором прямой l называется любой ненулевой вектор , перпендикулярный этой прямой.

Пусть заданы точка и нормальный вектор

(рис. 50). Для составления уравнения прямой, про­ходящей через точку М₁ и имеющей нормальный вектор п, вос-

145

Преобразуем это уравнение:

откуда

Далее, имеем

— уравнение прямой AD в общем виде.

146

8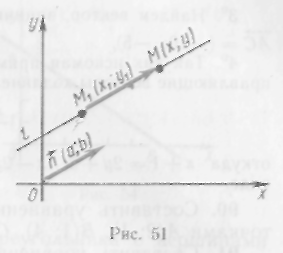 7. Составить уравнение серединного перпендикуляра к отрезку, заданному точками Л(2; 4) и В(5; -7)

6. Уравнение прямой,

Проходящей через

данную точку и

имеющей заданный

направляющий вектор

Направляющим

вектором прямой

называется всякий

ненулевой вектор , параллельный этой прямой. Любая прямая имеет беско­нечное множество направляющих векторов, коллинеарных между собой.

Пусть заданы точка , через которую проходит пря-

мая I (рис. 51), и ее направляющий вектор

Используя общее правило, составим уравнение прямой .

Преобразуем это уравнение:

Полагая , получим

— уравнение общего вида.

88. Составить уравнение прямой, проходящей через точку А(3; —2) и имеющей направляющий вектор

откуда — искомое уравнение в общем виде.

89. Треугольник задан точками А(5; 2)> В(—1; —4)- С(—5; -3). Составить уравнение прямой, проходящей через точку В параллельно АС.

147