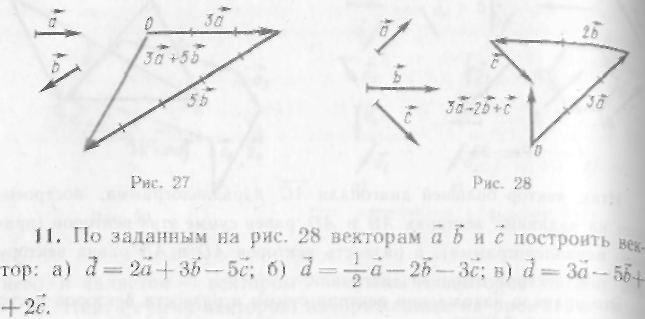Глава III Векторы и координаты

§ 1. Векторы и действия над ними

• 1. Векторные величины. Понятие вектора

• 2. Действия над векторами

• 3. Разложение вектора в базисе

• 4. Декартова система координат

1. Векторные величины. Понятие вектора

Некоторые физические величины (сила, скорость, ускорение) характеризуются не только числовым значением, но и направ­лением. Например, чтобы охарактеризовать движение тела в дан­ный момент, недостаточно указать скорость движения, а нужно еще указать направление движения тела, т. е. направление ско­рости. Таким образом, скорость является векторной величиной. Другими примерами векторных величин могут служить сила при­тяжения, центробежное ускорение и т. п.

Если на некотором отрезке задано начало отрезка и его конец, то такой отрезок называется направленным. Р Любой направленный отрезок называется вектором.

Вектор, заданный парой несовпадающих точек А и В, обозна­чается , причем в этой записи А — начало вектора, В — его конец.

Векторы могут быть записаны с помощью строчных букв:

1. Записать векторы, изображенные на рис. 14.

125

ка. Так как длина вектора обозначается , то часто

вместо «длина вектора» говорят «модуль вектора».

Обратим внимание на то, что длина вектора зависит от длины отрезка и не зависит от направления.

Мы видим, что длина нулевого вектора равна нулю: \АА\ = о.

Таким образом, каждый вектор, отличный от нулевого, имеет свою длину и направление.

Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Так, на рис. 15 коллинеарными являются следующие векторы:

Мы видим, что среди коллинеарных векторов есть такие, у которых направления совпадают. Эти векторы называют сонаправленными и пишут _. Если направления векторов

противоположно направлены, то их и называют противоположно

направленными и пишут

Два коллинеарных вектора называют равными, если они со-

направлены и имеют равные длины; другими словами,

если

Справедливы следующие утверждения:

Любой вектор равен самому себе, т. е.

Если два вектора по отдельности равны третьему, то они рав­ны между собой, т. е. если

126

2. Действия над векторами

Суммой векторов называется такой вектор , начало

которого совпадает с началом вектора , а конец — с концом вектора , при условии, что начало вектора перенесено в конец вектора .

Таким образом, чтобы сложить два вектора , нужно

выбрать на плоскости произвольную точку М и отложить от нее

вектор , а затем от точки А отложить вектор

Тогда вектор является искомой суммой векторов, _, т. е.

(рис. 17).

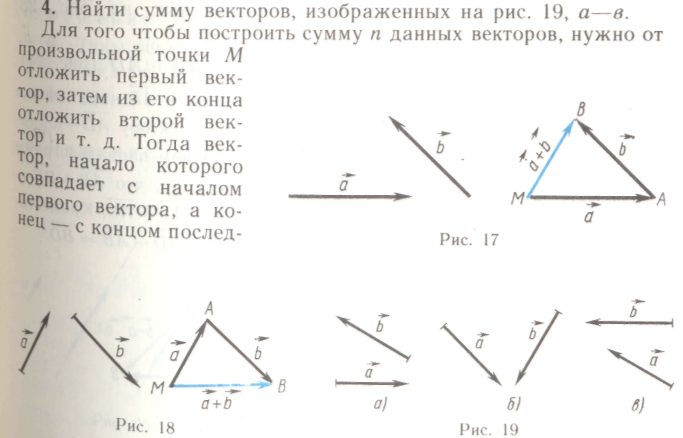
3. Сложить векторы , изображенные на рис. 18. Решение. Возьмем произвольную точку М и отложим от нее

Вектор . Из конца А этого вектора отложим вектор . Соединив точку М с концом В вектора , получим вектор, представляющий собой сумму векторов (рис. 18).

127

него, и является вектором суммы п векторов (рис. 20)

5. Найти сумму векторов, изображенных на рис. 21, а—в. Два вектора называются противоположными, если их сумма

равна нулевому вектору. Вектор, противоположный вектору

обозначают

Таким образом, противоположные векторы имеют равные длины и противоположно направлены.

Разностью векторов называют сумму вектора

т. е.

Чтобы найти разность векторов , нужно выбрать произ-

вольную точку М и отложить от нее векторы . Если соеди-

нить концы векторов , то получится вектор или

вектор (рис. 22).

6. Найти разность векторов, изображенных на рис. 23:

7. Построить сумму и разность векторов (рис. 24).

128

Итак вектор большей диагонали параллелограмма, построен на заданных векторах , равен сумме этих векторов (правило параллелограмма), а разность векторов равна вектору

т. е. вектору меньшей диагонали.

Это правило нахождения вектора суммы и разности векторов часто используется в физике.

5-1356 129