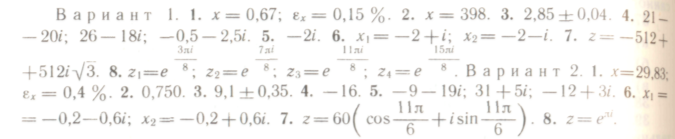Действия над комплексными числами в тригонометрической форме

Таким образом, при умножении двух комплексных чисел, задание тригонометрической форме, их модули перемножаются, документы складываются:

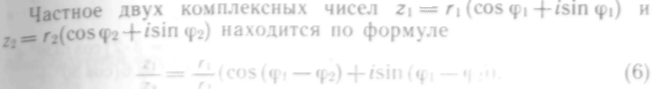
т е. при делении комплексных чисел, заданных в тригонометри­ческой форме, их модули делятся, а аргументы вычитаются:

Для возведения комплексного числа в n-ю степень используется формула, которая называется фор­мулой Муавра:

Следовательно, при возведении в степень комплексного числа, заданного в тригонометрической форме, модуль числа нужно вести в п-ю степень, а аргумент умножить на число п:

Корнем n-й степени из числа г (где п — натуральное число, большее или равное 2) называется такое комплексное число и, для которого справедливо равенство _.

Корень п-й степени из комплексного числа г имеет ровно п значений. которые находятся по формуле

117

(мы воспользовались свойством периодичности тригонометрических функций и отбросили полный период).

Итак,

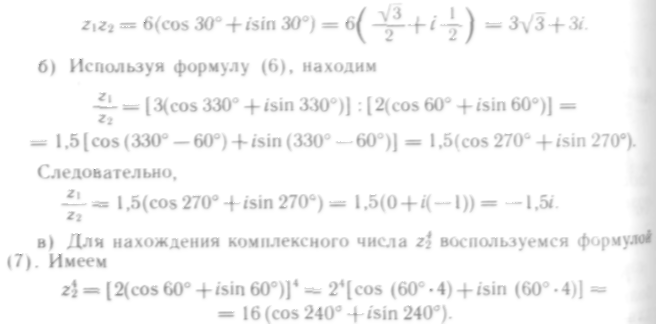
Используя формулы приведения, находим

Таким образом,

118

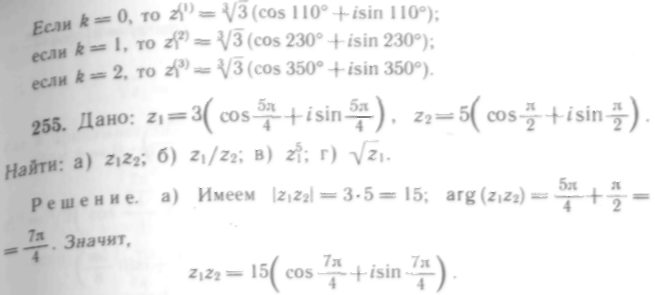
Воспользуемся формулами приведения:

Итак,

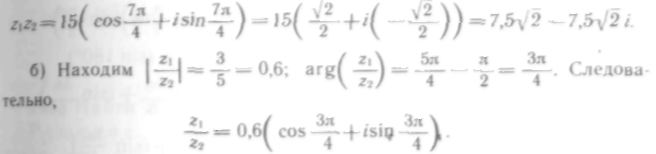
Воспользуемся формулами приведения:

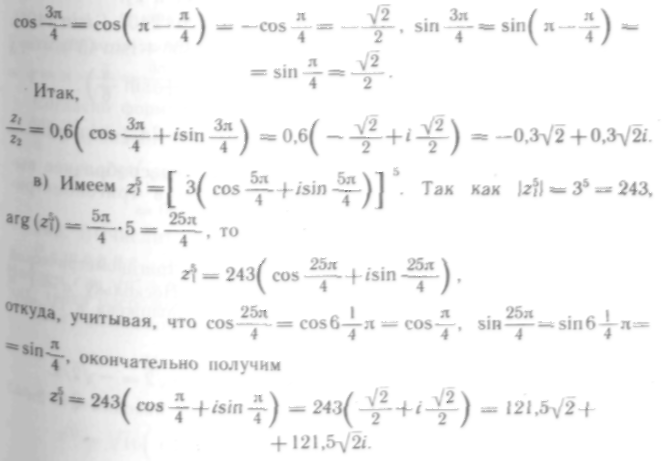
119

256—259. Найти произведение комплексных чисел Z₁ и Z₂.

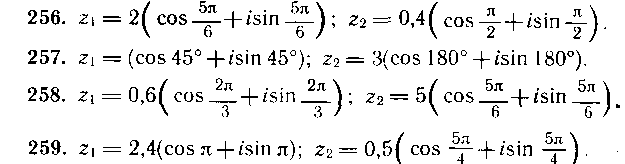
260—263. Найти частное комплексных чисел Z₁ и Z₂:

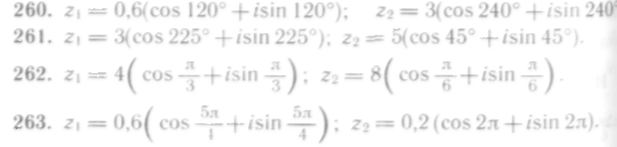
Мы уже убедились, что легче, а поэтому целесообразнее вы­полнять действия над комплексными числами в тригонометри­ческой форме.

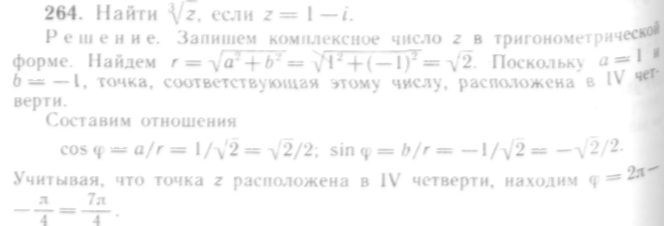
120

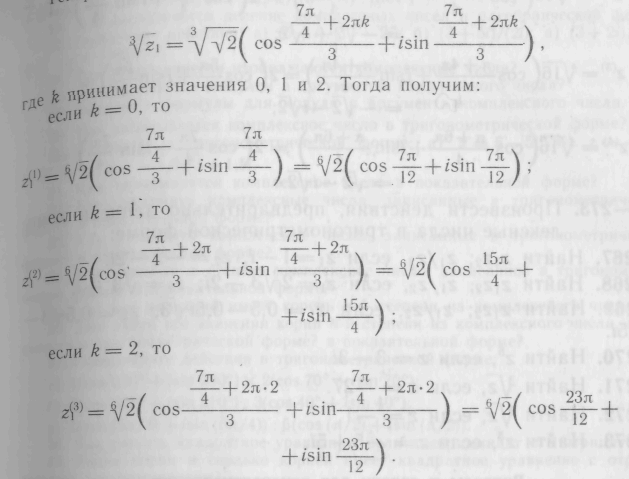
121

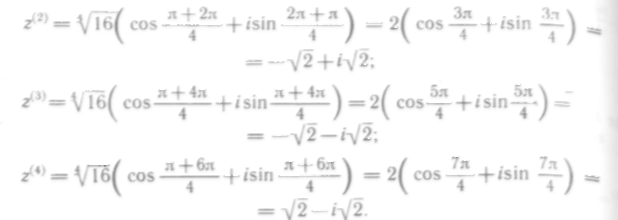
267—273. Произвести действия, предварительно записан комп­лексные числа в тригонометрической форме:

122

Ответы

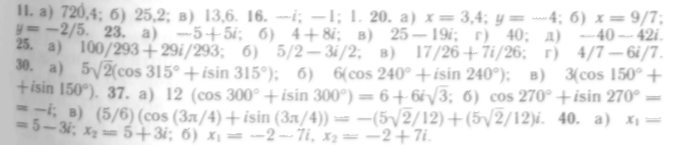
Контрольное задание

123

Вариант 2

Ответы