6. Действия с приближенными числами

Для того чтобы научиться производить действия с приближенными числами, нужно уметь находить погрешность этих действий. Сформулируем следующие правила:

I. Граница абсолютной погрешности суммы (разности) двух чисел равна сумме границ абсолютных погрешностей заданных чисел:

II. Граница абсолютной погрешности произведения двух чи­сел равна произведению границы относительной погрешности произведения на абсолютную величину произведения этих чисел

III. Граница абсолютной погрешности частного двух чисел равна произведению границы относительной погрешности частного на абсолютную величину частного этих чисел:

IV. Граница относительной погрешности произведения (частного) двух чисел равна сумме относительных погрешностей этих чисел:

V. Граница относительной погрешности степени равна произ- ведению границы относительной погрешности основания на по­казатель степени:

На практике пользуются более простыми правилами, называемыми правилами подсчета цифр:

I. При сложении и вычитании приближенных чисел в результате сохраняют столько десятичных знаков, сколько их в наименее точном числе.

II. При умножении и делении приближенных чисел в результате сохраняют столько значащих цифр, сколько их в числе с меньшим количеством значащих цифр.

III. При возведении в степень в результате сохраняют столько значащих цифр, сколько их в основании степени.

100

IV При извлечении корня сохраняют столько значащих

сколько их в подкоренном выражении.

V. При выполнении промежуточных действий оставляют на один знак больше, чем требуют правила, а в результате запасной знак округляют.

VI Если в вычислениях точность задана заранее, то вычисления ведут с запасным знаком, который в результате округляют.

119. Сложить приближенные числа:

101

7. Вычисления с помощью микрокалькулятора

Из предыдущих расчетов видно, что вычисления требуют большого количества времени, внимания и умения для выполне­ния арифметических действий. Эту работу значительно облегчает применение микрокалькуляторов.

Все микрокалькуляторы принято делить на три основные группы: простейшие (или бытовые), инженерные и программи­руемые.

Простейшие микрокалькуляторы предназначаются, как пра­вило, для выполнения арифметических операций и последова­тельностей таких операций. Более совершенные модели микро­калькуляторов могут иметь одну-две встроенные микропрограм­мы (обычно вычисление обратных величин, процентов, извлече­ние квадратного корня), а самые совершенные модели этой группы имеют также дополнительные регистры памяти, что во многих случаях может облегчить выполнение усложненных вы­числений.

К простейшим микрокалькуляторам относятся: БЗ-05; БЗ-14; БЗ-23; БЗ-24Г; БЗ-30; БЗ-39; СЗ-22; СЗ-33; МК-42; МК-44.

102

Инженерные микрокалькуляторы, предназначенные для более сложныx (научно-технических) расчетов, имеют значительное количество встроенных микропрограмм, обеспечивающих автоматическое вычисление много разрядных значений элементарных функций (показательных, логарифмических, прямых и обратных Фонометрических и некоторых других), дополнительные регистры памяти и в отдельных моделях — расширенные диапазо­ны представления чисел

К инженерным микрокалькуляторам относятся БЗ-18А; БЗ-18М; БЗ-19М; БЗ-32; БЗ-35 и т. д.

Программируемые микрокалькуляторы позволяют вычислителю ввести программу различных вычислительных процессов, том числе разветвленных и циклических, в несколько десятков команд, а затем многократно производить но этой программе вычисления при разных аргументах. Программируемые микро­калькуляторы в значительной степени заполняют разрыв между вычислительными возможностями обычных микрокалькуляторов и ЭВМ, компьютеров.

К программируемым микрокалькуляторам относятся БЗ-21; БЗ-34; МК-46; МК-56; МК-61.

Рассмотрим правила выполнения расчетов на простейшем микрокалькуляторе «Электроника СЗ-22».

Микрокалькулятор «Электроника СЗ-22» — миниатюрная на­стольная клавишная машина для индивидуального пользования при инженерно-экономических и бухгалтерских расчетах. Микро­калькулятор производит операции над двенадцатиразрядными десятичными положительными и отрицательными числами с естественным представлением запятой. Ввод информации кла­вишный. Микрокалькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, вычисление процента от числа, операции с использованием постоянных чисел, накоп­ление в памяти (последовательное сложение чисел, одно из кото­рых высвечивается на табло, а другое находится в памяти, являясь результатом предыдущего сложения). Среднее время выполнения одной операции составляет 0,6 с.

После включения машины в сеть необходимо тумблер «обще включение» на правой боковой стороне машины поставить в положение «вкл». После этого следует дважды нажать клавишу при этом на табло индикации в крайнем правом разряде высветится 0, что свидетельствует о готовности машины к работе.

Клавиатура работает от легкого, но четкого нажатия клавиш до упора.

Набор чисел производят начиная со старшего разряда. Для

Введения дробных чисел сначала набирают целую часть числа, том нажимают клавишу , затем дробную часть.

Если целая часть равна нулю, то ее можно не вводить и начинать набор числа с клавиши . Знак числа меняется после набора всего числа нажатием клавиши _. Если число

103

набрано неверно, то следует нажать клавишу; тогда машина сбрасывает последнее набранное число.

Выполнение простых операций:

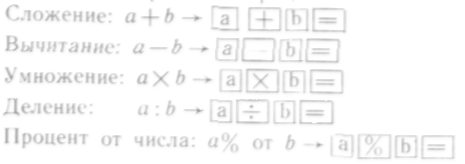
Выполнение более сложных операций производится в порядке их записи с учетом старшинства операций. Например:

Операции с постоянными числами производятся нажатием клавиши после ввода операции, при этом будет выполнено арифметическое действие, где вторым числом является постоян­ная величина.

Например, если k — постоянная величина, то

Для определения суммы заработка и премии в при заработке п руб. используется операция

С помощью этого приема можно легко производить серийное умножение и деление, расчет с постоянными процентами (вычис­ление налогов).

Для получения числа нужно произвести следующие операции:

При работе с клавишей«память» следует помнить, что в «памяти» может быть накоплено число, полученное в результате вычислений, и число, введенное с клавиатуры.

Пример выполнения вычисления с помощью «памяти»:

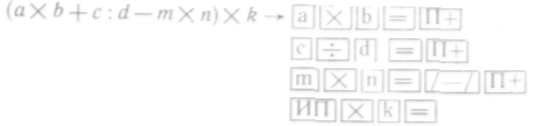
104