6. Решение примеров на все действия со степенями

120. Вычислить Решение. Выполним последовательно действия:

Используя полученные результаты, находим

121. Вычислить

122. Решение. Имеем:

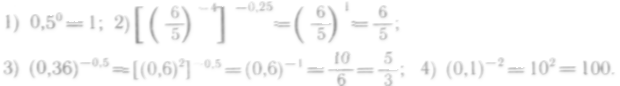
Подставив найденные значения, получим

122—128. Выполнить действия:

24

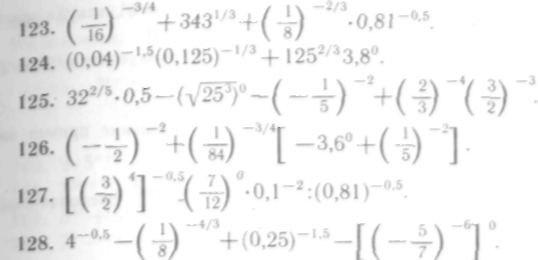
129. Сократить дробь

Решение. Разложив числитель и знаменатель дроби на множи­тели и сократив ее, получим

130—136. Упростить выражения:

7. Показательные уравнения

Показательными уравнениями называются такие уравнения, в которых неизвестное входит в показатель степени.

Показательные уравнения решаются после преобразований по правилам I—IV с использованием дробных, нулевых и отрицательных показателей степеней.

Сначала рассмотрим простейшие показательные уравнения, т.е. такие, левую и правую части которых сразу можно привести родному основанию.

137-178. Решить показательные уравнения:

137. 5^х= 625.

25

Решение. Записав 625 в виде , получим , откуда

Решение. Имеем ; . Следовательно, ,

Откуда , т. е.

139. 16*= 1/4.

Решение. Так как , , то уравнение примет вид

, откуда , т. е.

140.

Решение. Имеем ; следовательно,

141.

Решение. Любое отличное от нуля число в нулевой степени равно единице; поэтому можно записать 1=5,2°. Таким образом, , откуда . Согласно свойству произведения, или , т.е. .

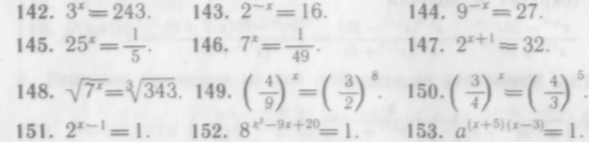
В более сложных случаях применяют правила I—IV.

154.

Решение. Приведем все степени к основанию 2: ; . Значит, . Применяя правило деления степеней, имеем

Следующий тип показательных уравнений решается вынесе­нием множителя с наименьшим показателем степени за скобки.

Решение. Так как наименьшим показателем степени является _, то вынесем за скобки:

Разделив обе части уравнения на 11, получим

26

Решение. Наименьшим показателем степени является ; поэтому вынесема скобки

Рассмотрим еще один тип показательных уравнений. Это — уравнение, которое с помощью подстановки сводится к квадратному уравнению.

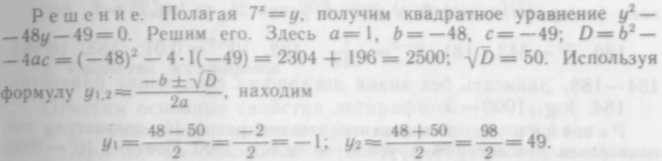
Так как (это равенство невозможно, поскольку показательная функция может принимать только положительные зна­чения); . Итак, получаем ответ:

§ 3. Логарифмы

• 1.Определение логарифма

• 2.Свойства логарифмов

• 3.Теоремы о логарифмах произведения, частного, степени и корня

• 4.Логарифмические уравнения

27

логарифму подкоренного выражения, деленному на показатель степени корня:

Прологарифмировать некоторое выражение, заданное в виде произведения, частного, степени или корня, — значит выразить логарифм этого выражения через логарифмы составляющих его чисел. Это позволяют сделать теоремы 1—4.

Так как в приведенных теоремах не рассматриваются лога­рифмы суммы или разности, то логарифмировать сумму или раз­ность будем как единое целое (не рассматривая логарифмы от­дельных чисел). 210—220. Прологарифмировать следующие выражения:

210.

Решение. Применив сначала теорему 2, а затем теоремы 1 и 3, получим

Здесь и в следующих-примерах основание логарифма мы не пишем, так как полученные равенства справедливы при любом основании.

211.

Решение. Применим последовательно теоремы 2, 1 и 3. На­ходим

212.

Решение. Применив теоремы 2, 1 и 3, получим

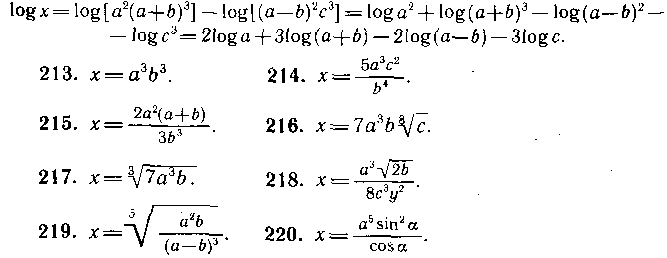
30

По данному результату логарифмирования мы можем найти исходное выражение. Это действие называется потенцированием.

221-228. По известному логарифму числа х найти это число:

221.

Решение. В силу утверждений, обратных теоремам 1 и 2, запи­шем

222.

Решение. Согласно утверждениям, обратным теоремам 3, 4, 1 и 2, получим

223. _.

Решение. Используя утверждения, обратные теоремам I, 3, 4 и 2, имеем

4. Логарифмические уравнения

Логарифмическим уравнением называется уравнение, в кото­ром неизвестное находится под знаком логарифма.

Такие уравнения решаются с помощью определения лога­рифма, теорем о логарифмах и утверждения, что если положи­тельные числа равны, то равны и их логарифмы при данном новации и, обратно, если равны логарифмы чисел при данном основании, то равны и соответствующие им числа.

При этом необходимо учитывать, что при любом а ( _, ) логарифмы отрицательных чисел и нуля не существуют.

229—240. Решить логарифмические уравнения:

31

Решение. Запишем данное уравнение в виде

Так как равны логарифмы и их основания, то равны и логарифмируемые числа:

Полагая , приведем дробь к общему знаменателю и решим полученное уравнение:

Подставив значение в уравнение, видим, что при этом значении х выражения отрицательны. Так как логарифмы отрицательных чисел не существуют, то — посторонний корень, а само уравнение не имеет решений.

Решение. Имеем

откуда

Корень является посторонним, поскольку при имеем и, следовательно, логарифмы этих выра­жений не существуют. Итак, получаем ответ:

Решение. Представив число 2 как логарифм числа 16 по осно­ванию 4, перепишем данное уравнение в виде

Отсюда получаем

Решаем это уравнение:

Для проверки подставим значение в данное уравнение:

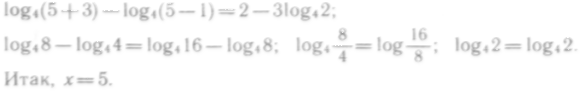
Рассмотрим еще один тип логарифмических уравнений.

32

Решение. Это логарифмическое уравнение, приводимое к квадратному. Полагая , получим уравнение

Здесь

. Используя формулу находим

Так как . Следовательно,