Лекция 8.Векторы в r . Элементы векторной алгебры

1. Скалярное произведение

Скалярным произведением вектора на вектор , обозначается , называется произведение модулей этих векторов на косинус угла между ними. Т.е.

= cos , (1)

где = ,угол

Если учесть, что *cos = = пр , а cos = пр , то соотношение (1) можно представить в иной эквивалентной форме

= пр = пр (2)

К числу основных можно отнести следующие свойства скалярного произведения:

1. переместительный закон = .

2. распределительный ( + )= +

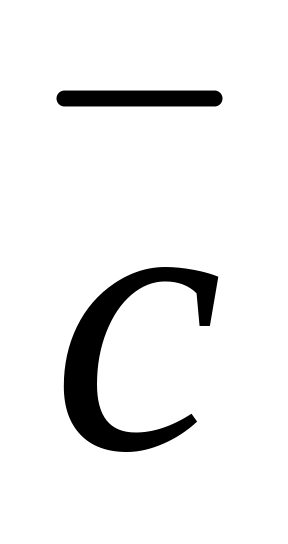3. сочетательный при умножении на число ( )= ( ) = ( ).

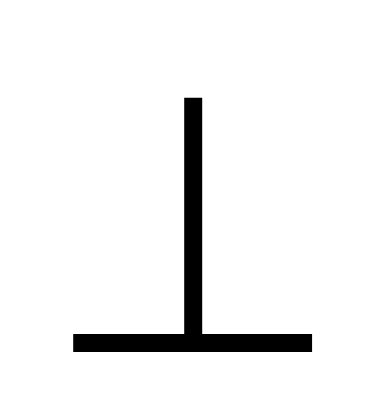
4. =0.

Из этих свойств дадим обоснование последнему.

Действительно, пусть . Тогда = , соs = 0 и, следовательно, = *cos =0. Обратно, пусть = cos =0.

Тогда возможны случаи:

1. соs =0. Отсюда = и ,следовательно ,

2. или = 0, т.е один из векторов или , нулевой.

Т.к направление нулевого вектора не определено, то и в данном случае мы можем считать, что он перпендикулярен второму вектору.

Физический (механический) смысл . Заключается в следующем. Пусть есть вектор силы, действующей на некоторую материальную точку, а вектор её перемещения под действием этой силы, тогда -это работа, выполненная силой по перемещению материальной точки из начальной в конечную точку вектора .

Вычисление ( ) через координаты векторов. Пусть = ( , , ), =( , , ). Рассмотрим разложения этих векторов по базису

= + + ,

= + + .

Тогда, учитывая, что

= = = 0,

= = = 0,

получим

= + + .

2. Векторное произведение

Векторным произведением вектора на вектор , обозначается , называется вектор , удовлетворяющий следующим условиям:

1. , ;

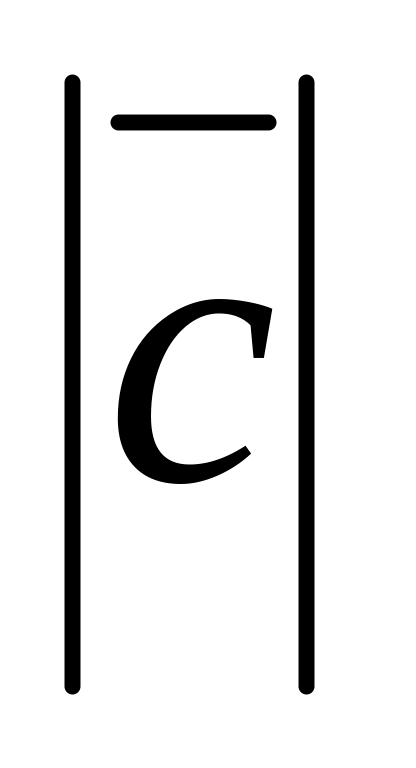2. = sin , где = ;

3. наблюдателю, помещённому в конечную точку вектора кратчайший поворот от вектора к вектору видится происходящим против часовой стрелки.

Иллюстрация к этому определению приводится на рисунке

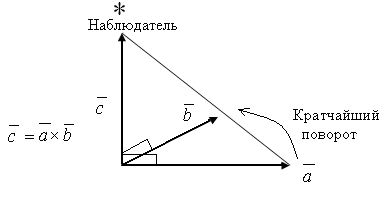
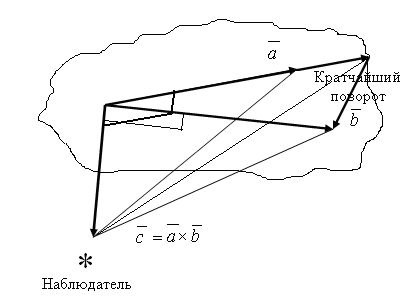
Укажем некоторые из свойств векторного произведения:

1. = ( ), антипереместительный закон

2. ( + )= + , распределительный закон

3. ( )= ( ) = ( ), сочетательный при умножении на число

4. =0 || .

Поясним последнее из них.

Пусть =0 | |= 0 sin = 0 sin = 0 или = 0 или = 0. Отсюда = 0 или , или один из векторов является нулевым и , следовательно, векторы коллинеарны.

Обратно, если || , то = 0 или и следовательно, =0. Таким образом , свойство 4 можно рассматривать, как необходимое и достаточное условие коллинеарности векторов.

Физический смысл . Если вектор является

радиус вектором материальной точки А относительно некоторого полюса О, а вектор силы, приложенной к точке А, то векторное произведение представляет собой момент силы относительно полюса О. Т.е.

mom = .

Геометрический смысл . Рассмотрим | |= sin , где = . Вспоминая известную геометрических формулу , можно утверждать, что модуль векторного произведения векторов и есть площадь параллелограмма, построенного на этих векторах как на сторонах, т.е.

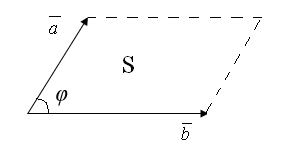
S= * *sin .

Таким образом, модуль векторного произведения равен площади параллелограмма , построенного на векторах и , как на сторонах.

Задача. Вычислить площадь параллелограмма, построенного на векторах и , если = 3 + 2 , = 2 - , | |= 4, | |= 3, =

Решение. Искомая площадь S= | |.

Отсюда:

S= |( 3 + 2 ) (2 - )|= | 3 2 - 3 + 2 2 - 2 |

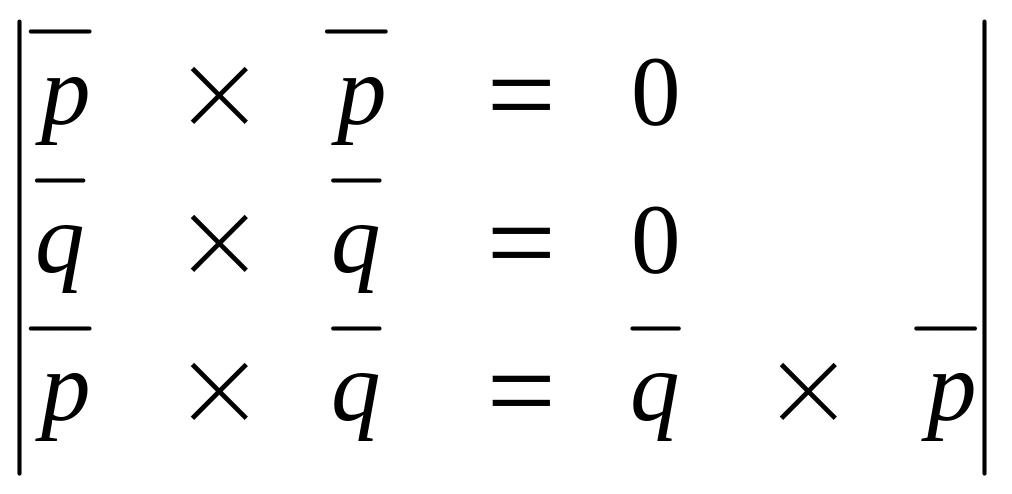= = 7 | |= 7 | | | | sin( )= 7 4 3 sin =

= 7 2 4 = 42

Ответ: S= 42 кв.ед.