Лабораторная работа 5. Решение задач оптимального управления динамическими экономическими системами Задачи динамического программирования

Задача динамического программирования (ДП) формулируется следующим образом: найти минимум (максимум) функции.

(21)

при ограничениях

(22)

Эта задача имеет следующую геометрическую интерпретацию. Введем семейство прямых, каждая из которых со

ответствует переменной x_i.

Теперь задача минимизации аддитивной функции свелась к поиску ломаной кратчайшей длины, соединяющей прямые x₀ и x_1. Каждая дуга этой ломаной, соединяющей некоторые точки представляет собой одно из слагаемых в сумме.

Рисунок 18. Задача динамического программирования

Идея метода динамического программирования и более общего метода последовательного анализа вариантов состоит в возможности минимизировать не всю сумму (рис. 18) по всем переменным, а только пару слагаемых из нее по одной переменной. Цена за эту возможность-необходимость ее решения n+1 раз.

Другая интерпретация метода динамического программирования состоит в возможности находить оптимальные решения в задачах минимизации функционального вида , встречающихся в теории оптимального управления. В дискретном варианте интервал интегрирования разбивается на N шагов с достаточно малым интервалом дискретным временем , и величина интеграла может быть представлена формулой трапеций в виде

что представляет собой аддитивную функцию от переменных u_i, i=

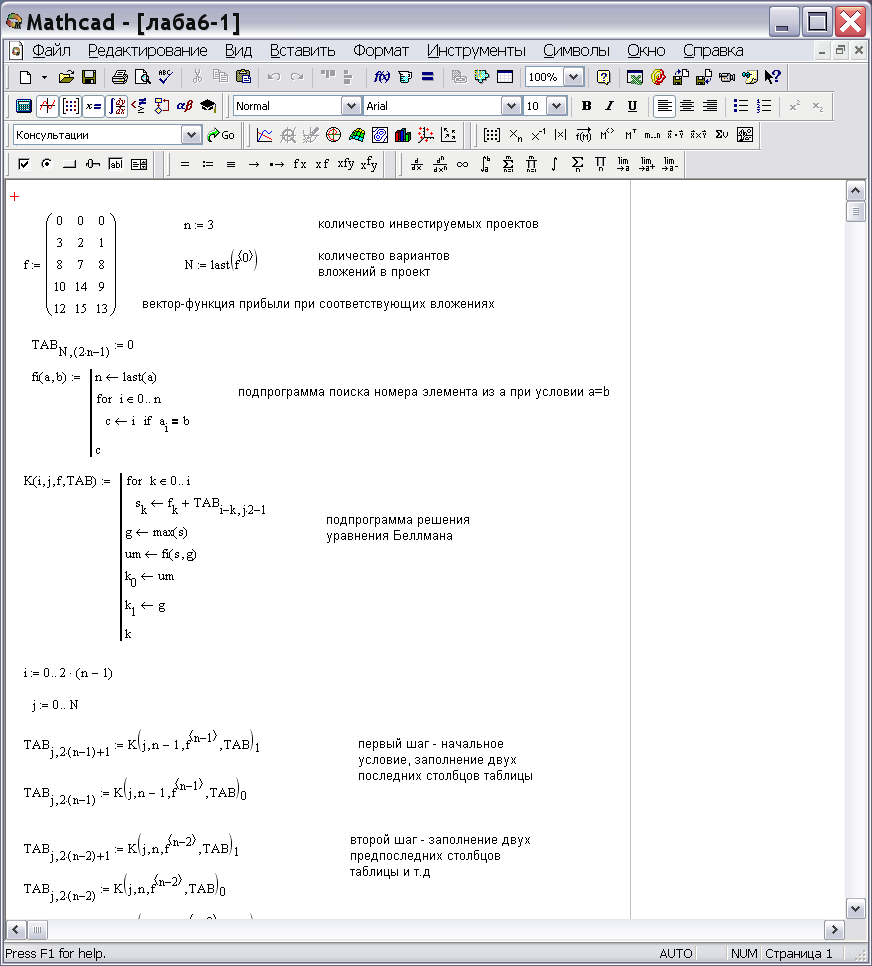
Лабораторная работа 6. Решение задачи об оптимальном распределении ресурсов

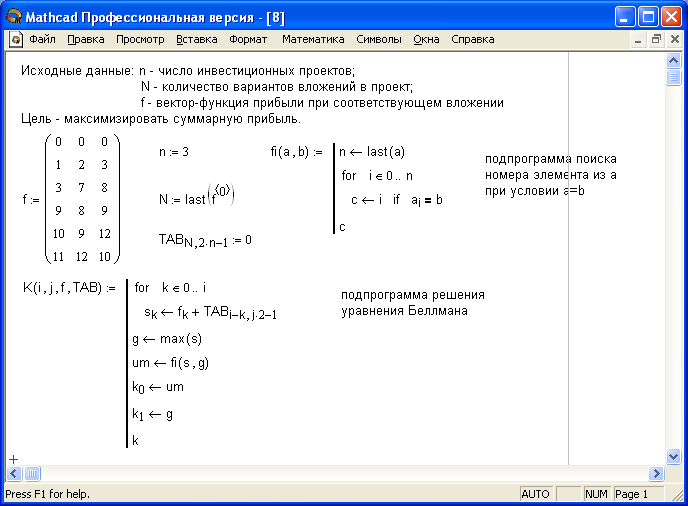Пусть имеется инвестиционных проектов и сумма средств для инвестиций . Прибыль от каждого проекта задана функцией , , - вложения в каждый проект. Должна быть максимизирована суммарная прибыль от всех проектов

(2.7)

при условии

(23)

На рис. 19 приведен документ MathCAD, в котором реализован пример решения задачи распределения ресурса.

Рис. 19– Решение задачи распределения ресурса

Лабораторная работа 7. Оптимизация межотраслевого баланса

Возможность оптимизации МОБ появляется, если коэффициенты прямых затрат отражают затраты не средние по отрасли, а для каждого способа и технологии производства. В таких моделях МОБ представлено отдельно производство мартеновской, конверторной стали, а также электростали; синтетических и хлопчатобумажных тканей и т. д. В результате должен быть найден оптимальный вариант с минимальными затратами на производство данного объема продукции. Применение методов линейного программирования

Оптимизацию межотраслевого баланса покажем на примере сведения балансовых задач к задачам линейного программирования.

Пусть, как и ранее, заданы векторы X, Y и матрица А связанные матричным уравнением.

Допустим, что конечный продукт Y задан не точно, а ограничен снизу, т. е. Y В.

Тогда система уравнений заменится неравенствами

(Е - А)Х В. (24)

Очевидно X 0. Пусть задан вектор

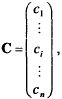
где — оценка единицы продукта й отрасли, тогда можно сформировать следующую задачу линейного программирования. Выбрать ассортиментный вектор X 0, удовлетворяющий системе неравенств (24), для которого линейная функция

(25)

достигает минимума.

Рассмотрим линейную балансовую модель, характеризующуюся матрицей (n = 3):

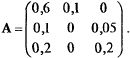
Необходимо обеспечить производство конечного продукта, удовлетворяющее ограничению Y В = (180, 130, 220). Производственные мощности 1- и 2-й отраслей ограничивают их валовый выпуск: 400, 300. Валовый выпуск 3-й отрасли практически неограничен.

Определить оптимальный валовый выпуск продукции, т. е. вектор Х= , при котором линейная функция достигает максимума.

Задача принимает вид

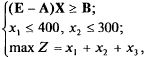
или

Модель МОБ как многосвязной системы

Рассмотренная постановка задачи ЛП характерна для централизованного управления системой в целом. В случае же автономности отраслей возникают задачи анализа на точку равновесия и выработки оптимального координирующего воздействия (см. гл. 3).

Сформулируем данную задачу в обозначениях гл. 3. Имеется n отраслей, я отрасль выпускает продукт в количестве 0.

На выпуск единицы продукта затрачивается продукта , где — постоянные коэффициенты, . Чистый выпуск продукта

Каждая отрасль стремиться обеспечить выпуск Проанализируем систему на существование точки Нэша.

Примечание: обычно матрица удовлетворяет следующим условиям:

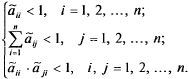
Индикатор цели для го элемента

В матричной форме

Решение уравнения существует и , если существует

Известно, что подобный ряд сходится [16], если одна из норм меньше 1. В данном случае таковой является норма:

Следовательно, точка равновесия по Нэшу существует и единственна.

З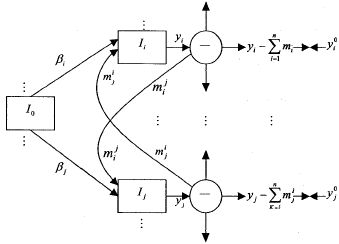 адача координации межотраслевого баланса

Рассмотрим нелинейную модель межотраслевого баланса — замкнутую параллельно-последовательную систему (рис. 20). Каждая отрасль производит продукта го типа,

затрачивая продуктов отраслей

в том числе собственный продукт в количестве .

Рисунок 20. Нелинейная модель межотраслевого баланса

Глобальная цель состоит в удовлетворении планируемого конечного спроса , т. е. задан индикатор глобальной цели

Оптимальный координирующий сигнал обеспечивает = 0.

Производственная функция й отрасли:

Координация состоит в назначении цен на продукты. Локальная цель состоит в максимизации прибыли:

Определим оптимальный координирующий сигнал . Исследуем возможность существования в зависимости от свойств и матрицы

Локальная целевая функция й подсистемы в переменных m

Условия экстремума функций (m)

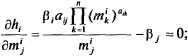
Отсюда

Подставив данное соотношение в левую часть уравнения , получим

Далее, обозначив

перепишем уравнение в виде

откуда

где

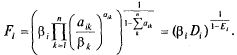
Исследуем полученный результат. Общий выпуск го продукта в оптимальной точке:

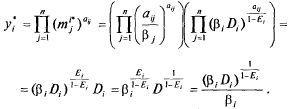
Окончательно

В стоимостной форме оптимальный выпуск

Затраты й отрасли в стоимостной форме

Прибыль й отрасли

Если < 1, т. е. < 1, то прибыль положительна.

Далее, й ресурс потребляется в размерах натурального исчисления

и денежного

Тот же ресурс (продукт) производится в размерах исчислений натурального и денежного

Всего в денежном исчислении производится , а потребляется .

Система обладает валовой продуктивностью [26], если

Система продуктивна по му ресурсу (продукту), если

.

Поскольку цель системы — удовлетворение некоего конечного спроса

в натуральном исчислении, то система уравнений

в зависимости от А может иметь или не иметь решение

определяя существование оптимального координирующего сигнала.

Сравним рассматриваемую в настоящей задаче модель с линейной моделью (см. выше).

Коэффициенты (элементы матрицы ) являются коэффициентами прямых затрат.

В денежном исчислении есть отношение стоимости го продукта, потребляемого й отраслью, к общей стоимости производимого продукта.

В рассматриваемом случае

Таким образом, в системе, отрасли которой стремятся максимизировать прибыль, является транспозицией матрицы