16.2.2. Angle of attack of airplane zero lift

The value of angle of attack of airplane zero lift is included in general expression for the airplane lift coefficient (16.7) and is calculated under the formulae:

, (16.12)

, (16.13)

where , , , - angles of attack of zero lift of the fuselage, wing, horizontal tail and engine nacelle in the airplane system. At that, angle of fuselage zero lift corresponds to the angle of isolated fuselage zero lift , angle of engine nacelle zero lift - to angle of the engine nacelle axis installation relatively to the fuselage axis (at axis deflection upwards ).

The angles of attack and also depend on airplane configuration:

- for the normal configuration:

,

; (16.14)

- for the canard configuration:

,

, (16.14)

where and - angles of zero lift for the isolated wing and horizontal tail (usually ), and - angles of wing and horizontal tail setting relatively to the fuselage axis; - also can be the angle of pivot stabilizer deflection.

16.2.3. Maximum airplane lift

Maximum lift and critical angle of attack met to it are the parameters determining airplane performance. The precisely values of the maximum lift coefficient and critical angle of attack now can be obtained only in experimental way.

For the airplane with high-aspect-ratio wings values are calculated under the formula

, (16.15)

where - characteristic of the wing airfoil; the factors take into account influence of the airfoil shape, sweep angle, wing taper and flight Mach number.

For the airplane with low-aspect-ratio wing the maximum lift coefficient is calculated by the formula

. (16.16)

The critical angle of attack of the airplane with the high-aspect-ratio wing and with low-aspect-ratio wing without the account of non-linear effects is determined as follows

, (16.17)

where and - airplane characteristic.

The construction of ratio by known values , and is shown in fig. 16.2.

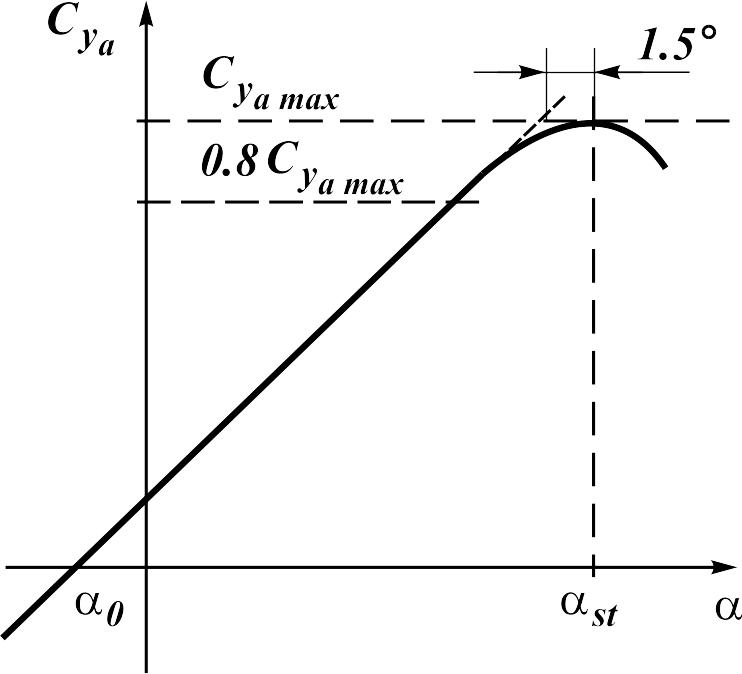
Fig. 16.2. A construction of ratio

16.3. Polar of a aircraft.

The origin of inductive drag is connected to formation of a vortex wake behind a skew field at presence of lift. However on a wing with geometric twist a vortex wake and inductive drag can exist when the summarized lift of a wing will be equal to zero.

The factor of the airplane induced drag can be presented in the following form:

, (16.18)

where the first item concerns to the airplane, which basic elements creating lift have horizontal plane of symmetry and lifting surfaces set under zero angle to the fuselage axis; - factor of induced drag at .

The additional items, as a rule, introduce the minor contribution to induced drag for majority of airplanes in flight configurations, i.e. it is possible to accept and , and for such case

,

where - polar pull-off coefficient.

At subsonic Mach numbers the value is determined as follows

, (16.19)

where - wing aspect ratio with ventral part.

Parameter depends on the cross section shape of the wing - fuselage configuration. The factor takes into account the horizontal tail contribution into induced drag.

For isolated wing with the optimum (elliptical) law of circulation distribution spanwise we shall have , , and in accordance with (16.19) we come to known result .

In a supersonic flow the polar pull-off coefficient is calculated as follows

, (16.20)

where - relative factor of sucking force realized on the fuselage nose at absence of the nose air intake, on wing subsonic leading edges and horizontal tail.

The characteristic ratio of the polar pull-off coefficient on Mach number is shown in fig. 16.3. Let's note, that the polar pull-off coefficient practically does not vary at subsonic speeds, at supersonic speeds it is increased, because the derivative of the lift coefficient decreases.

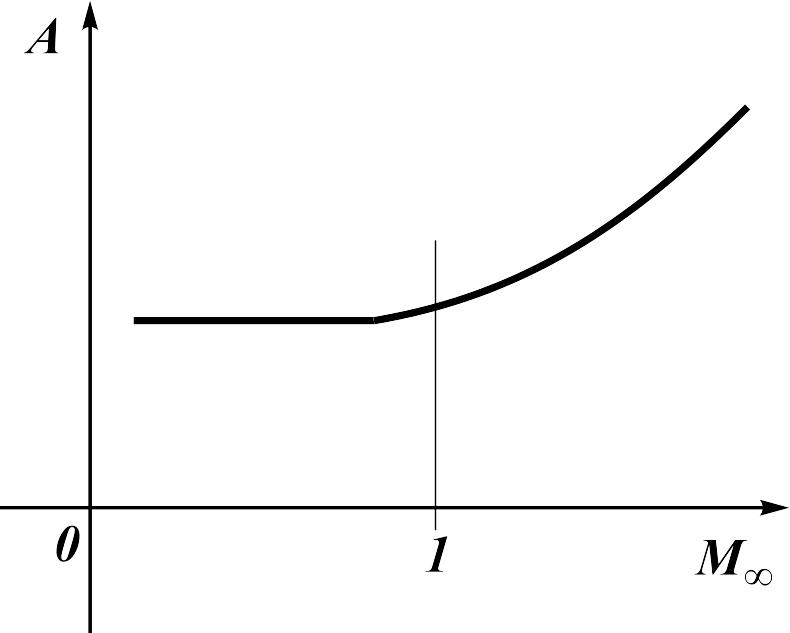
Fig. 16.3. Polar pull-off factor on Mach number ratio

It is necessary to take into account the additional drag which is conditioned by angles of attack influence onto profile drag and wave crisis happening on the wing for the airplane polar construction.

The updated expression for calculation of a polar looks like

. (16.21)

The increment of the profile drag factor with angles of attack increasing zis estimated as follows

, . (16.22)

The second source of additional drag is connected to local shock waves happened on the wing at values of a lift coefficient which is going out of subsonic speeds range, which boundary is determined by ratio (fig. 6.22). The additional drag is determined by the formula

, (16.23)

where is determined by the formula (6.23).

The account of additional drag results in the characteristic fork of polars constructed for various flight numbers . The higher the number , the smaller values of the deviation from the subsonic polar. In transonic flow area ( ) already at the wave drag appears and the polar top displaces to the right.

The characteristic polar types are shown in fig. 16.4 and fig. 16.5.

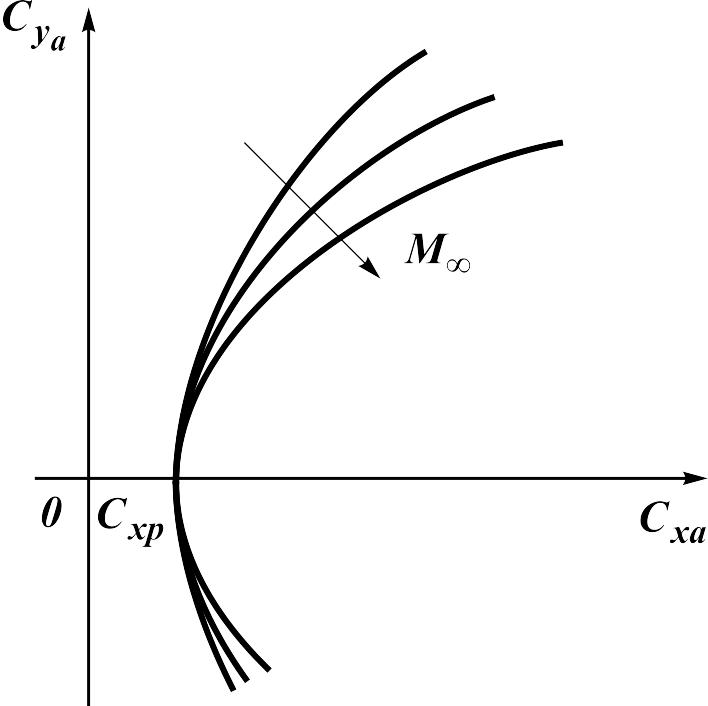
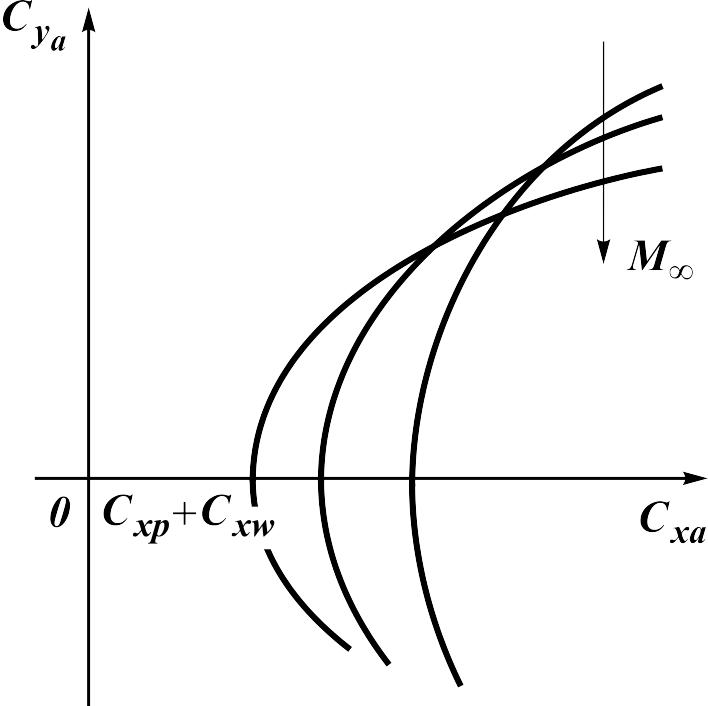
Fig. 16.3. The airplane polar in subsonic range of speeds

Fig. 16.4. The airplane polar in supersonic range of speeds

By known values of factors and also calculate airplane lift-to-drag ratio . The value of maximum quality is determined with the help of expression .