§4. Ранг матрицы
Имеется матрица Аmn порядка mn и не все элементы ее равны 0. (aij 0).
Пусть существует минор rго порядка, который не равен нулю, и при этом любой минор порядка большего r равен нулю, т.е. Mr 0, Mr + i = 0 (i =1, 2,… , n – r) .
Минор Mr называется базисным минором матрицы А (он необязательно единственный), строки и столбцы, выбором которых получен минор называются базисными строками и столбцами, число r называется рангом матрицы А: r = rangA. Другими словами rangА – это наибольший порядок отличного от нуля минора этой матрицы.
6. Теорема о базисном миноре. Строки базисного минора – линейно независимы, и любая строка матрицы А является линейной комбинацией базисных строк.
Примечание: Теорема может быть сформулирована и доказана не только для строк, но и для столбцов.
◀ 1) Пусть rangA = r. Не ограничивая общности можно считать, что первые r строк матрицы a1, a2,…, ar – базисные. Докажем их линейную независимость.
Пусть
1a1
+ 2a2
+…+ rar
=
и пусть 1
0. Тогда a1
=
,
т.е.
первая строка является линейной
комбинацией остальных, но тогда detMr
= 0, что
противоречит базисности минора Mr
.
Значит 1 = 2 =…= r = 0 и, следовательно, базисные строки матрицы линейно независимы.
2) Пусть rangA = r и базисный минор Mr стоит в левом верхнем углу:
.
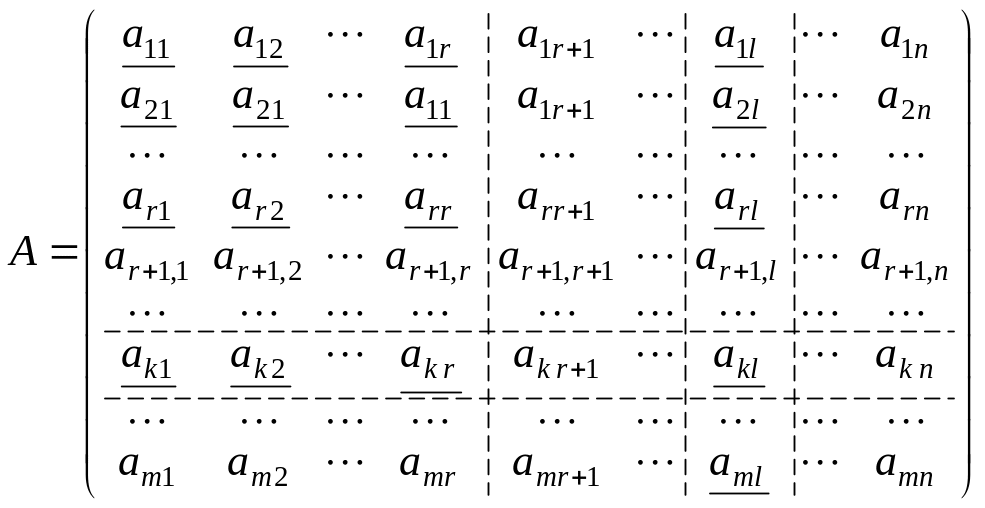Рассмотрим определитель (r + 1)го порядка, состоящий из подчеркнутых элементов: Ar+1.
По условию базисности минора Mr detAr+1 = 0.
Разложим
определитель Ar+1
по последнему столбцу. a1lA1l
+ … + arlArl
+ aklAkl
= 0; При этом
Akl
0 (это detMr).
Тогда
.
Обозначим
;
;
Akl
–
это минор
Mr
и не зависит
ни от k,
ни от l.
Ail
—
не зависит
от l
(при вычитании выбрасывается). Тогда
c1,
c2,
...
cr
не зависит
от l,
а зависит
только от k.
Имеем akl
= с1a1l
+ с2a2l
+...+
crarl.
Последнее равенство показывает, что
элементы kй
строки выражены через элементы первых
r
строк.
▶
Из этой теоремы следует, что:
7. detA = 0 тогда и только тогда, когда его строки (столбцы) линейно зависимы.
8. rangA = dimℒ(a1, a2, … , am) = dimℒ(s1, s2, … , sn); a1, a2, … , am – строки; s1, s2, … , sn – столбцы.
§5. Преобразования, не изменяющие ранг матрицы
Следующие преобразования не изменяют ранг матрицы:
1) Транспонирование. ◀ При транспонировании определитель не меняется и поэтому, минорам равным нулю будет поставлено в соответствии миноры, равные нулю, а минорам не равным нулю будут соответствовать миноры, не равные нулю (0 0 и 0 0). ▶
2) Перестановка двух строк (столбцов). ◀ Любой минор – это полилинейный антисимметричный функционал (а1, а2, …, ak, …, aj, …, ar) = – (а1, а2, …, ak, …, aj, …, ar).
Отсюда ясно, что 0 0 и 0 0. ▶
3) Умножение всех элементов строки (столбца) на число C ≠ 0 .
◀ (a1, a2, …, cak, …, ar) = c(a1, a2, …, ak , …, ar) 0 0 и 0 0. ▶
4) Прибавление ко всем элементам одной строки (столбца) соответствующих элементов другой строки (столбца). ◀ Не ограничивая общности, можно считать, что к элементам 1й строки прибавляются элементы 2й строки
(a1+ a2, a2, a3 ,…,ar) = (a1, a2, …, ar) + (a1 a2, a3 ,…, ar) = (a1, a2,…, ar). ▶
5) Вычеркивание нулевой строки (столбца). ◀ Включение в систему векторов нулевого вектора или выбрасывание нулевого вектора не изменяет dimℒ(a1, a2 ,…, ar). ▶
6) Вычеркивание строки (столбца), являющейся линейной комбинацией остальных.
◀ Достаточно воспользоваться свойствами 3), 4) и 5). ▶