Задание №7.
1. Найти
скорость и направление наибыстрейшего
возрастания поля
в точке М(-1,
2, 1).
2.
Убедиться в ортогональности поверхностей
уровня полей:
.
3. Найти
поток векторного поля
через расположенную в первом октанте
часть сферы
.
4. Найти
дивергенцию векторного поля
в точке М(3,2,-1).
5.
Установить потенциальность поля
и найти его потенциал.
6. Найти
ротор векторного поля
,
если
,
.
7. Найти
дивергенцию градиента скалярного поля
.
8.
Показать, что поле вектора
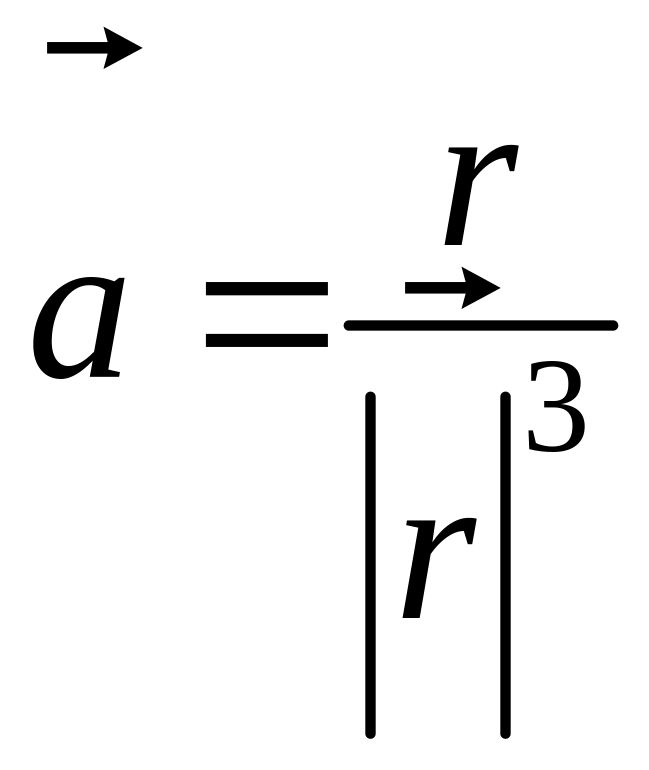является соленоидным и потенциальным,
если
.
Найти потенциал этого поля.
9. Найти
векторные линии плоского поля
.
10. Найти
ротор векторного поля
в точке М(2,3,4). Является ли данное поле
соленоидным?
11.
Проверить является ли точка М(1,1,2)
источником поля
.
12.
Вычислить поток векторного поля
через внешнюю сторону треугольника
АВС, полученного при пересечении
плоскости
с координатными плоскостями.
13.
Проверить является ли векторное поле
гармоническим.
14. Найти
циркуляцию вихря вектора
по контуру, состоящему из дуги параболы
и отрезку прямой
в положительном направлении.
15.
Проверить формулу Стокса для поля
вектора
принимая за контур интегрирования
окружность
,
а за поверхность интегрирования – часть
плоскости Oxz,
ограниченной этой окружностью.
16. Найти
поток вектора
:
а) через полную поверхность призмы,
получающейся при пересечении плоскостей
в направлении внешней нормали, б) через
верхнее основание этой призмы в
направлении оси Oz.
17.
Показать, что поле градиентов скалярной
функции
является безвихревым.
18. Найти
работу силы
вдоль ломанной ОАВ, где О(0,0,0), А(1,1,1) и
В(2,3,4).
19. Найти
поток вектора
через полную поверхность тела,
ограниченного поверхностями
в направлении внешней нормали.
20. Найти
,
где
.
21. Найти
векторные линии поля градиентов функции
.
22.
Вычислить поток вектора
через основание цилиндра
,
расположенное в плоскости
в направлении оси Оу.
23. Будет
ли точка М(0,1,1) источником или стоком
поля
.
24. С
помощью теоремы Остроградского вычислить
поток векторного поля
через поверхность тела, ограниченного
поверхностями
.
25. Найти
производную поля
в точке М(-1, 1, 1) в направлении вектора
,
если
.