Задание №5.

1. Вычислить криволинейный интеграл по дуге кривой от точки (1,1) до точки (2,4).

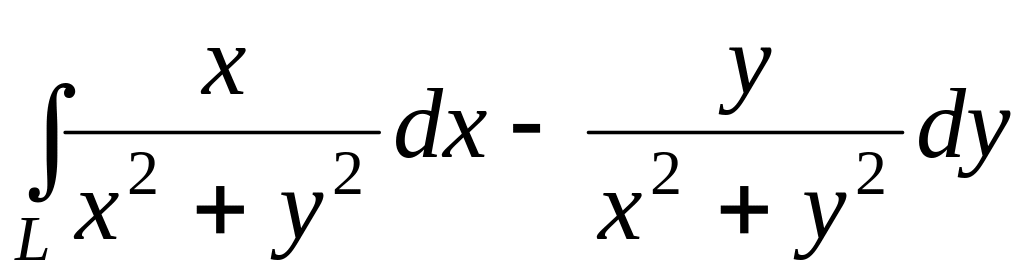2. Вычислить по окружности с центром в начале координат и радиусом R.

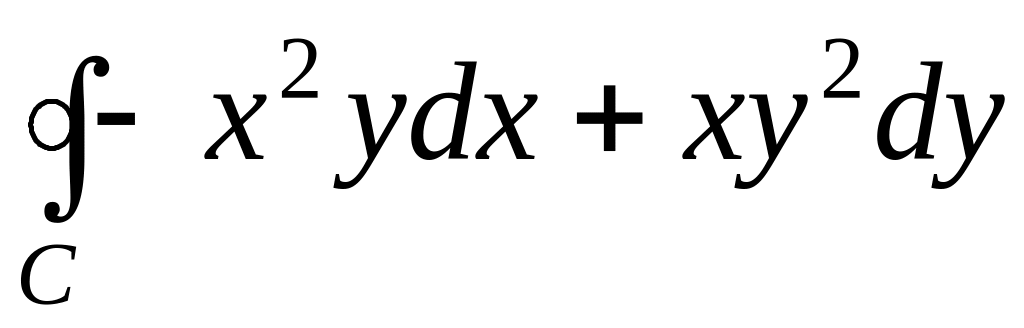
3. Применяя формулу Грина, вычислить , где С – окружность .

4. Вычислить 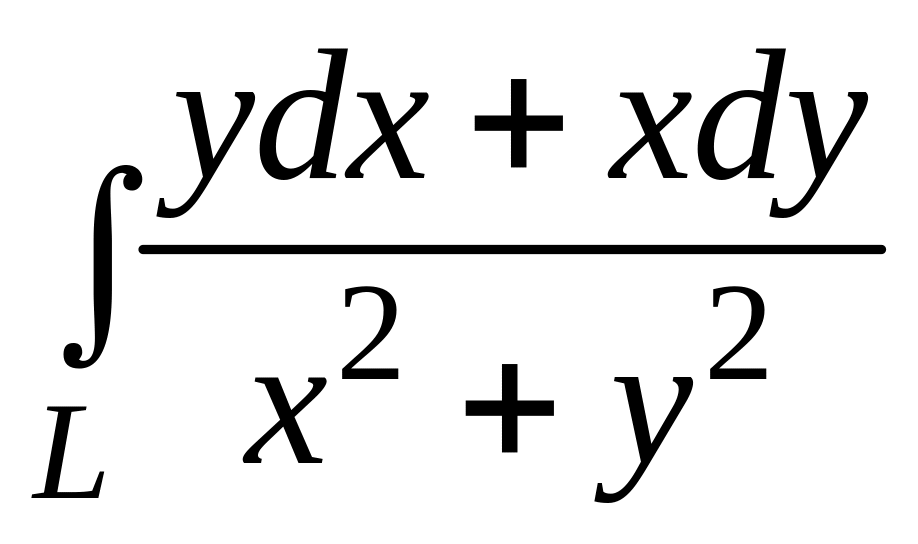по отрезку прямой от до .

5. Вычислить , где L – контур прямоугольника с вершинами О(0,0), В(4,0), С(4,2) и D(0,2).

6. Вычислить криволинейный интеграл 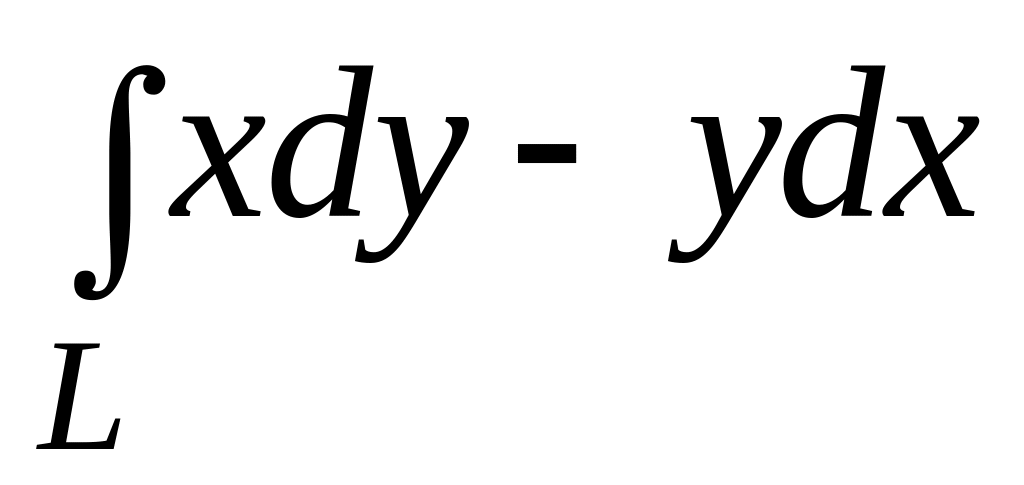по дуге кривой 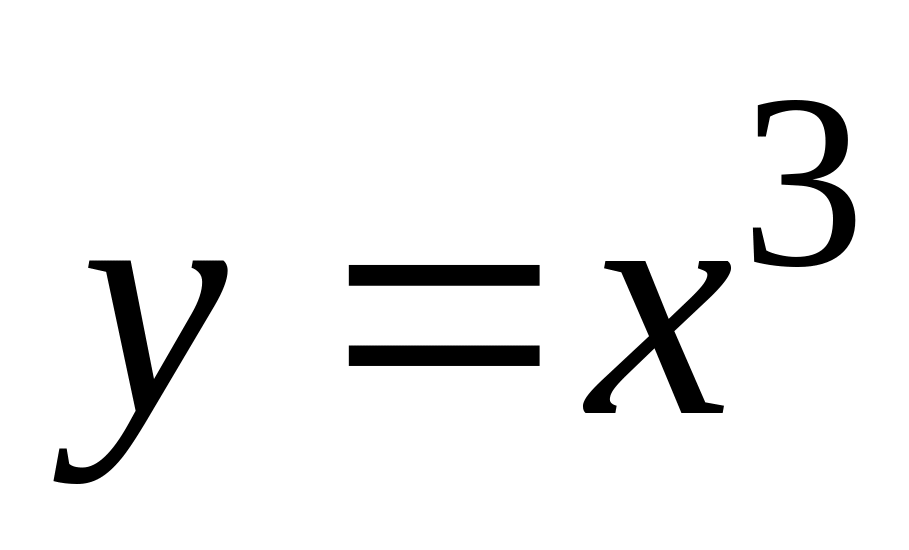от точки А(1,1) до точки В(2,8).

7. Вычислить криволинейный интеграл по кривой .

8. Найти , где L – первый виток линии .

9. Поле образовано силой . Показать, что работа при перемещении материальной точки в этом поле не зависит от пути.

10. Найти , если путь интегрирования – верхняя половина окружности между точками .

11. Найти по контуру треугольника, ограниченного осями координат и прямой .

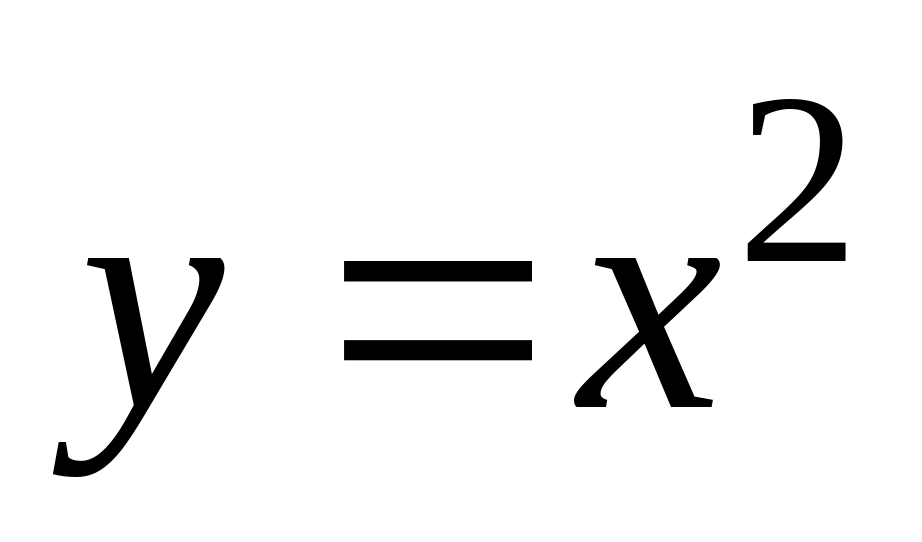12. Найти по дуге кривой от точки А(2,4) до точки В(1,1).

13. C помощью криволинейного интеграла найти площадь, ограниченную астроидой

14. Найти по периметру прямоугольника: .

15. Найти от точки М₁(0,0) до точки М₂(1,2) по кривой .

16. Найти вдоль прямой линии.

17. С помощью криволинейного интеграла найти площадь, ограниченную кардиоидой: .

18. Найти , где l – первая арка циклоиды .

19. Вычислить криволинейный интеграл по периметру треугольника ОАВ с вершинами в точках О(0,0), А(1,0), В(0,1) (против хода часовой стрелки).

20. Вычислить криволинейный интеграл вдоль линий: .

21. Вычислить по отрезку от точки(0,-2) до точки (4,0).

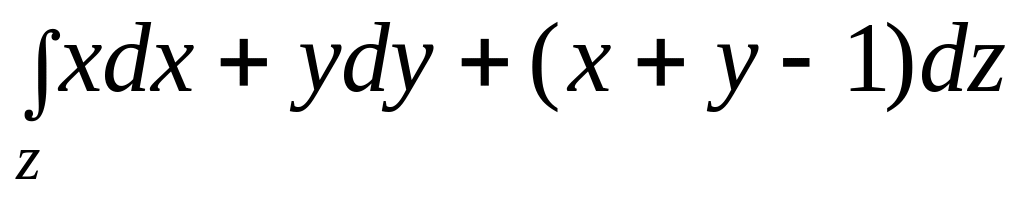22. Вычислить , где z – отрезок прямой от точки (1, 1, 1) до точки В(2, 3, 4).

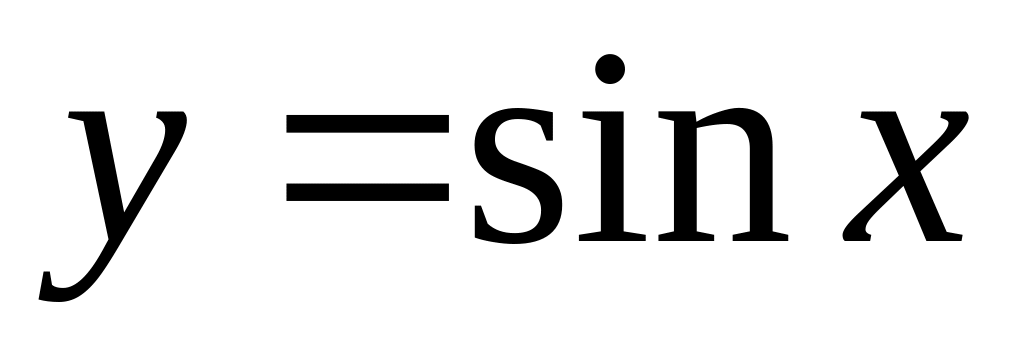23. Вычислить криволинейный интеграл по дуге кривой от до x=0.

24. Вычислить криволинейный интеграл по кривой от точки (0, 0) до точки В(2, 4).

25. Вычислить криволинейный интеграл 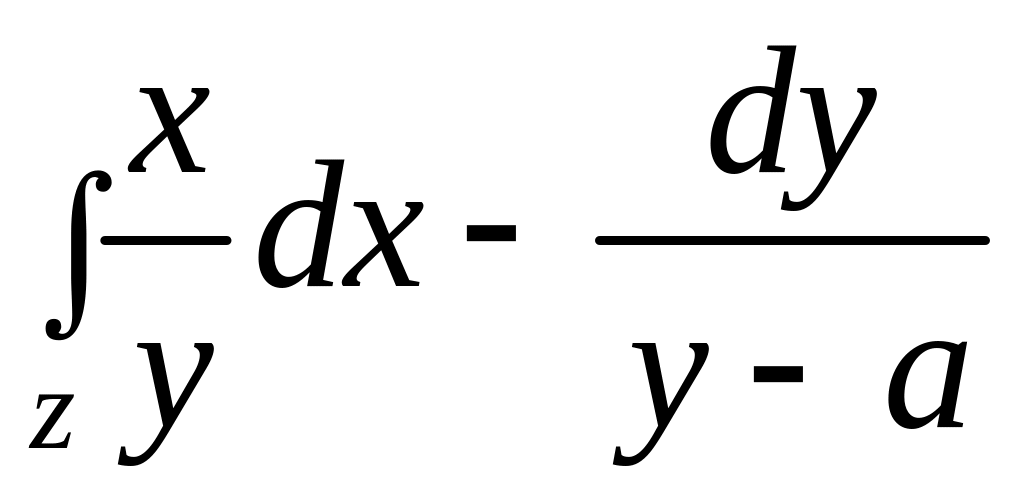по дуге циклоиды от точки 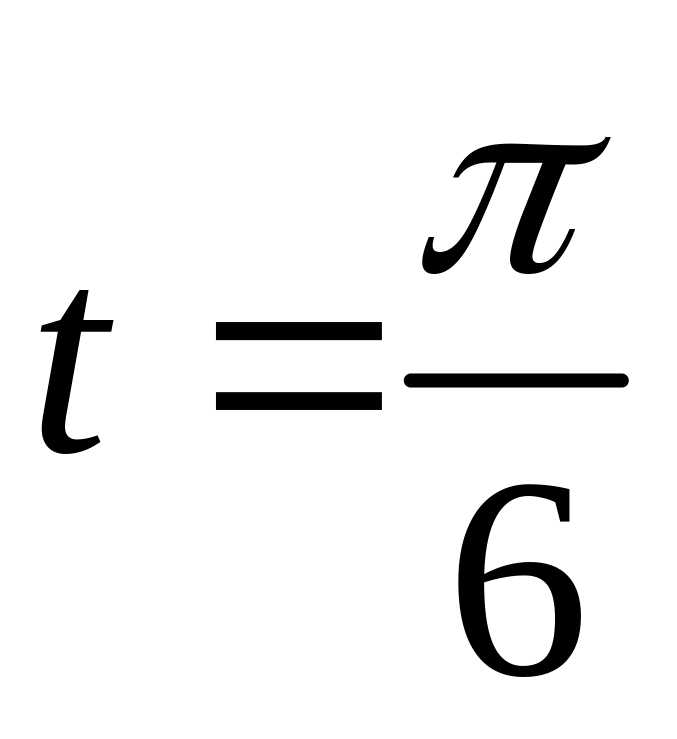до точки .

Задание №6.

1. Найти центр тяжести треугольника (равнобедренного прямоугольного), если в каждой его точке поверхностная плотность пропорциональна расстоянию ее до гипотенузы.

2. Найти центр тяжести однородной усеченной призмы, ограниченной координатными плоскостями и плоскостями .

3. Найти центр тяжести прямоугольного треугольника, катеты которого a и b, если в каждой его точке поверхностная плотность пропорциональна квадрату расстояния ее от вершины прямого угла.

4. Найти центр тяжести однородного тетраэдра, ограниченного плоскостями .

5. Найти координаты центра тяжести дуги АВ винтовой линии , если в каждой ее точке линейная плотность пропорциональна аппликате этой точки, .

6. Найти координаты центра тяжести однородной поверхности , отсеченной плоскостями z=0 и z=h.

7. Найти центр тяжести полусферы , если в каждой ее точке поверхностная плотность пропорциональна квадрату расстояния этой точки от радиуса, перпендикулярного основанию полусферы.

8. Найти координаты центра тяжести однородного тела, ограниченного поверхностями .

9. Найти координаты центра тяжести, однородной дуги кривой .

10. Найти координаты центра тяжести однородного тела, ограниченного параболоидом и плоскостью .

11. Найти координаты центра тяжести однородной дуги циклоиды .

12. Найти центр тяжести треугольника (равнобедренного прямоугольного), если в каждой его точке поверхностная плотность пропорциональна расстоянию ее до гипотенузы.

13. Найти центр тяжести однородной усеченной призмы, ограниченной координатными плоскостями и плоскостями .

14. Найти центр тяжести прямоугольного треугольника, катеты которого a и в, если в каждой его точке поверхностная плотность пропорциональна квадрату расстояния ее от вершины прямого угла.

15. Найти центр тяжести однородного тетраэдра, ограниченного плоскостями .

16. Найти координаты центра тяжести дуги АВ винтовой линии , если в каждой ее точке линейная плотность пропорциональна аппликате этой точки, .

17. Найти координаты центра тяжести однородной поверхности , отсеченной плоскостями z=0 и z=h.

18. Найти центр тяжести полусферы , если в каждой ее точке поверхностная плотность пропорциональна квадрату расстояния этой точки от радиуса, перпендикулярного основанию полусферы.

19. Найти координаты центра тяжести однородного тела, ограниченного поверхностями .

20. Найти координаты центра тяжести, однородной дуги кривой .

21. Найти координаты центра тяжести однородного тела, ограниченного параболоидом и плоскостью .

22. Найти координаты центра тяжести однородного тела, ограниченного поверхностями: .

23. Найти координаты центра тяжести однородной дуги циклоиды .

24. Найти координаты центра тяжести конической поверхности , если ее плотность в каждой точке пропорциональна расстоянию этой точки от оси конуса.

25. Найти центр тяжести однородного шарового слоя, заключенного между сферой и плоскостями и .