25

Тема: ТОК В РАЗЛИЧНЫХ СРЕДАХ

1. Ток в металлах

§1. Природа носителей тока в металлах.

Мы уже неоднократно говорили, что носителями тока в металлах являются электроны. Ионы кристаллической решетки не принимают участия в переносе заряда.

Опытные доказательства этого факта были получены лишь в начале ХХ века.

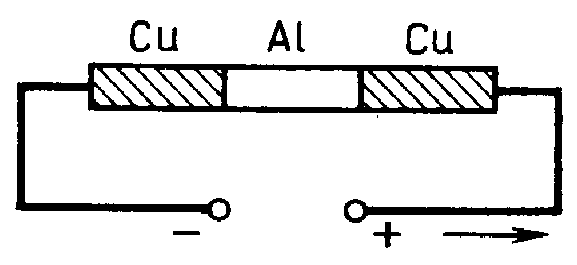
1. 1901г., опыт Рике. По цепи из медных и алюминиевых цилиндров, плотно подогнанных друг к другу, больше года пропускался электрический ток в сотни ампер – по цепи прошло 3,5·10⁶ Кл. Взвешивание цилиндров до и после опыта показало, что масса цилиндров не изменилась (с точностью до 3·10^-5 г). Следовательно, переноса вещества ионами нет. Можно было предположить, что заряд переносится электронами. Но чтобы это доказать, надо было определить значение удельного заряда носителей тока (удельный заряд – это отношение заряда к массе частицы).

2) Наиболее убедительное доказательство электронной природы тока в металлах получено в опытах с инерцией электронов.

И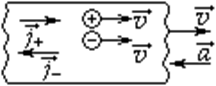 дея опыта: если металл, движущийся с большой скоростью, резко затормозить, то легкие электроны по инерции продолжат движение, т.е. в металле появится ток. По направлению тока можно судить о знаке заряда носителей.

Идею опыта высказали в 1913 г. Российские физики Мандельштам и Папалекси, а количественные измерения отношения заряда носителей к их массе провели в 1916 г. Толмен и Стюарт в Америке.

К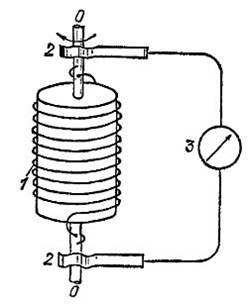 атушка (1) с большим числом витков приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью скользящих контактов (2) присоединялись к баллистическому гальванометру (3), по отбросу стрелки которого можно было судить о протекшем через него заряде. При резком торможении катушки в цепи возникал кратковременный ток.

По величине протекшего по цепи заряда удалось измерить отношение е/m и подтвердить, что носители тока в металлах – отрицательные электроны.

Демонстрация: модель опыта Толмена и Стюарта – раскручивается спираль с водой; при резком торможении вода выливается.

§2. Классическая теория электропроводности металлов Друде-Лоренца

Исходя из представления о свободных электронах, Друде и Лоренц в начале ХХ века создали теорию электропроводности металлов.

В этой теории предполагается, что свободные электроны ведут себя как молекулы идеального газа. Они почти не взаимодействуют друг с другом, а их взаимодействие с решеткой сводится к соударениям, и это приводит к тепловому равновесию между электронным газом и кристаллической решеткой.

Предполагалось также, что электроны в металле подчиняются законам классической механики и классической статистической физики.

В промежутках между столкновениями они движутся свободно, пробегая в среднем некоторый путь l (его называют длиной свободного пробега). Время свободного пробега – это среднее время движения от соударения до соударения.

Под действием электрического поля движение электронов представляет собой сумму теплового (со скоростью u) и упорядоченного (со скоростью v) движений, причем v<<u. Средняя скорость упорядоченного движения определяет плотность тока. Найдем . Забудем пока что о тепловом движении, благо оно хаотично и поэтому не влияет на .

П од действием электрической силы электроны движутся с ускорением и за время свободного пробега приобретают скорость

. (1)

В этой теории предполагается, что в результате каждого соударения электроны теряют всю скорость упорядоченного движения и начинают затем вновь разгоняться полем. Таким образом, средняя скорость упорядоченного движения

.

Отношение называют подвижностью носителей тока.

Плотность тока

.

Плотность тока пропорциональна напряженности поля, как и утверждает закон Ома в дифференциальной форме:

,

где и – удельная проводимость и удельное сопротивление, равные, соответственно:

, (2).

Найдем теперь удельную тепловую мощность тока. При соударениях с ионами решетки электроны, ускоренные полем, передают им всю свою кинетическую энергию упорядоченного движения (обратите внимание: плотность тока определяется средней скоростью упорядоченного движения, а передаваемая иону решетки энергия – максимальной). За одну секунду каждый электрон испытывает в среднем соударений. Умножив на частоту соударений и на концентрацию свободных электронов, найдем удельную тепловую мощность тока:

(мы воспользовались формулой (1) для ).

Итак, мы получили закон Джоуля-Ленца в дифференциальной форме.