О заряде внутри проводника с током
В случае стационарного (обычно говорят
«постоянного») тока внутри однородного
проводника нет нескомпенсированных
зарядов, т.е. объемная плотность заряда
равна нулю:
.
Это утверждение следует из теоремы
Остроградского-Гаусса, закона Ома (1) и
уравнения непрерывности. Итак:
для стационарных токов ;
по закону Ома
,
причем в однородном проводнике
.
Отсюда получаем:
,
или
.
Но по теореме Остроградского-Гаусса
,
значит,
.
Итак, при протекании постоянного тока весь нескомпенсированный заряд распределяется только по поверхности. Избыточный заряд находится также в местах соприкосновения различных проводников.
Электрическое поле проводника с током
Внутри проводника с током имеется электрическое поле, линии которого, если проводник однородный, в точности повторяют линии тока. Это поле создается зарядами, распределенными по поверхности проводника с током.
В случае стационарного тока распределение заряда по поверхности проводника не изменяется со временем, поэтому электрическое поле стационарного тока потенциальное, как и электростатическое поле.
Так как тангенциальная составляющая
вследствие потенциальности поля
непрерывна (см. параграф «Граничные
условия» в теме «Диэлектрики»), можно
сделать вывод, что снаружи проводника
вблизи его поверхности у вектора
имеется тангенциальная составляющая,
равная полю внутри проводника:
.
А так как на поверхности проводника
есть нескомпенсированные заряды, то
вблизи поверхности у вектора
есть и нормальная составляющая
.
Поэтому вектор
вблизи проводника направлен под некоторым
углом к его поверхности.
З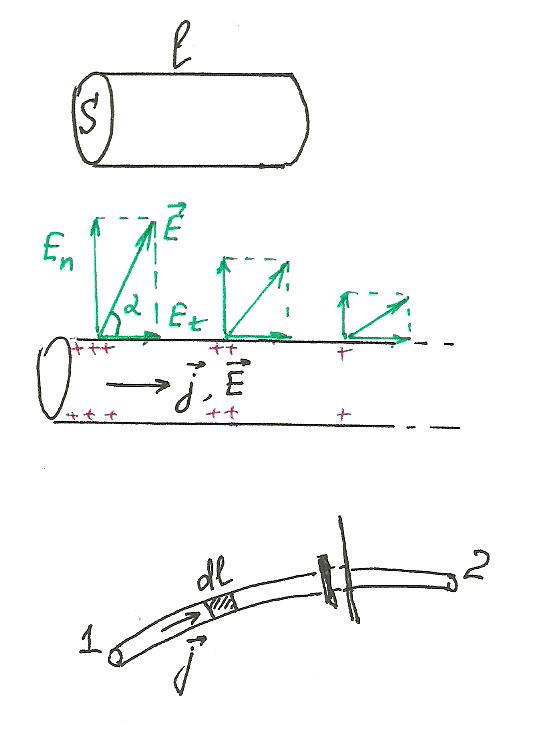
аряд
по поверхности проводника с током
распределен неравномерно – его
поверхностная плотность
убывает в направлении протекания тока.
А так как
,
то и
убывает, и угол между вектором
и поверхностью проводника постепенно
уменьшается.
Демонстрация. О распределении заряда по поверхности длинного цилиндрического проводника можно судить по углу расхождения подвешенных к нему лепестков из фольги. Если проводник заряжен статически, угол расхождения всех лепестков один и от же. При протекании тока этот угол уменьшается по направлению тока.
§ 3. Стационарные токи в однородной проводящей среде
Рассмотрим трубку тока в однородной
проводящей среде. Плотность тока j
в произвольном нормальном сечении
трубки связана с силой тока I
и площадью сечения
соотношением:
,
причем сила тока одна и та же в любом сечении, если ток стационарный (иначе заряд накапливался бы между двумя сечениями трубки).
З
апишем
закон Ома в локальной форме:
,
или
(1).
Умножим обе части уравнения (1) на элемент длины dl трубки тока и проинтегрируем по всей длине трубки от начального сечения 1 до конечного 2, двигаясь по току, т.е. вдоль линии напряженности:
(2).
Интеграл в левой части уравнения (2) есть
разность потенциалов
(или напряжение
)
между концами 1 и 2, интеграл в правой
части, зависящий от формы и размеров
трубки и удельного сопротивления среды,
называют сопротивлением данного
участка трубки – обозначим его
.
Итак, мы получаем:
,
или
(3),
где
(4).
Это соотношение называют законом Ома в интегральной форме.
Сопротивление однородного проводника цилиндрической формы, как следует из (4), равно
,
где l – длина проводника, S – площадь его нормального сечения.
Единица измерения сопротивления в СИ – 1 Ом. Как видно из закона Ома (3), Ом=В/м.