Тема: ПОСТОЯННЫЙ ТОК
§ 1. Плотность тока, сила тока, уравнение непрерывности
Электрический ток – это упорядоченное движение зарядов – носителей тока.
Носители тока: в металлах – свободные электроны,
в электролитах – ионы обоих знаков,
в газах – электроны и ионы, в полупроводниках – электроны и дырки.
Будем пока что считать, что все носители одинаковы (электроны в металлах).
В отсутствие электрического поля носители участвуют только в тепловом движении и средний вектор их скорости равен нулю.
В электрическом поле появляется отличный
от нуля вектор средней скорости
электронов, направленный против поля
(т.к. заряд носителей отрицательный).
Эту скорость называют дрейфовой
(или скоростью упорядоченного движения
носителей). Обозначим ее
.
Л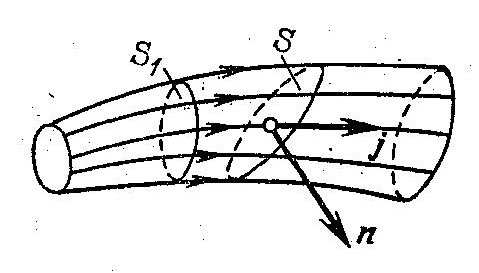
инии,
касательные к которым в каждой точке
совпадают с направлением
,
называют линиями тока. Линии тока,
проходящие через некоторый замкнутый
контур, образуют трубку тока.
Плотность тока j – это заряд, переносимый за единицу времени через единицу площади нормального сечения трубки тока.
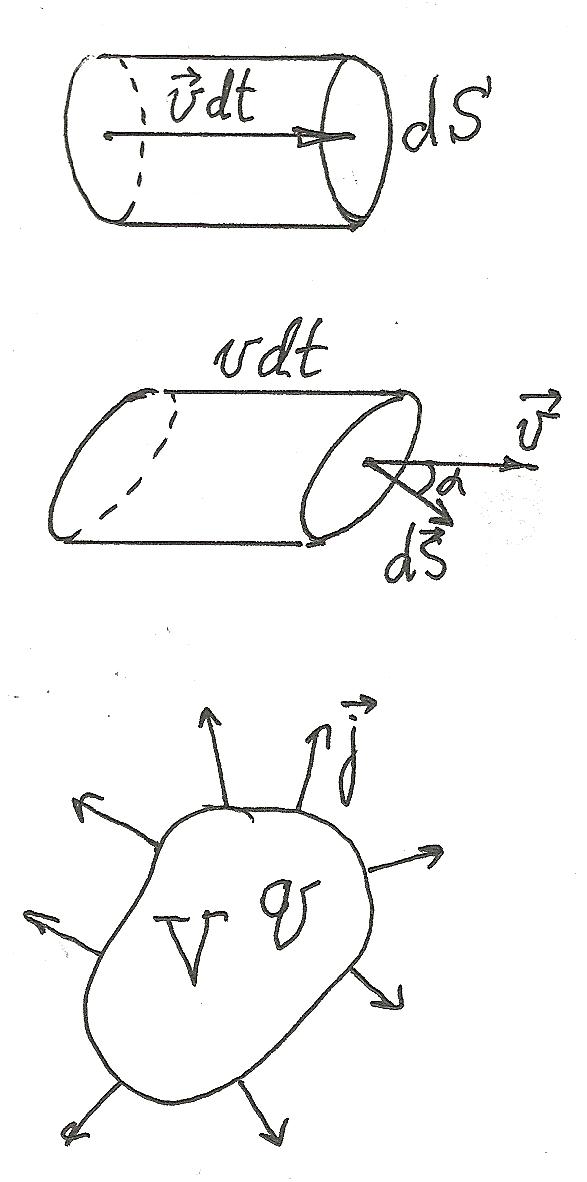
Пусть n – концентрация носителей, dS – площадь нормального (т.е. перпендикулярного линиям тока) сечения трубки тока. За время dt через эту площадку протечет заряд dq=env·dt·dS. Плотность тока
.
Плотность тока принято считать вектором, направленным в сторону вектора дрейфовой скорости положительно заряженных носителей или противоположно скорости отрицательных носителей, поэтому в металлах
.
Если нормаль сечения трубки тока образует
угол
с линиями тока, то
.
Сила тока – это скалярная физическая величина, равная заряду, протекающему через произвольное сечение S проводника за единицу времени:
.
Единица измерения силы тока – Ампер – основная в СИ. Ее определение будет дано позже, при рассмотрении магнитного взаимодействия токов.
Уравнение непрерывности
Выражает локальный характер закона сохранения заряда. Это значит, что заряд не может исчезнуть в одном месте и появиться в другом, но он должен протечь из первого места во второе.
Итак, пусть S – произвольная замкнутая поверхность в проводящей среде, в которой течет ток. За время dt из нее вытекает заряд dq, причем
.
Тогда внутри этой поверхности заряд
изменится на величину
.
Поэтому
.
Это и есть уравнение непрерывности. В
дифференциальной форме оно принимает
вид:
,
где
– объемная плотность заряда.
Важное следствие: в случае стационарного
тока (плотность тока во всех точках
среды не меняется со временем) поток
вектора
через любую замкнутую поверхность равен
нулю:
,
а также
.
Заряд не может накапливаться внутри замкнутой поверхности; сколько линий тока в нее входит, столько же и выходит.
§ 2. Закон Ома в дифференциальной (локальной) форме
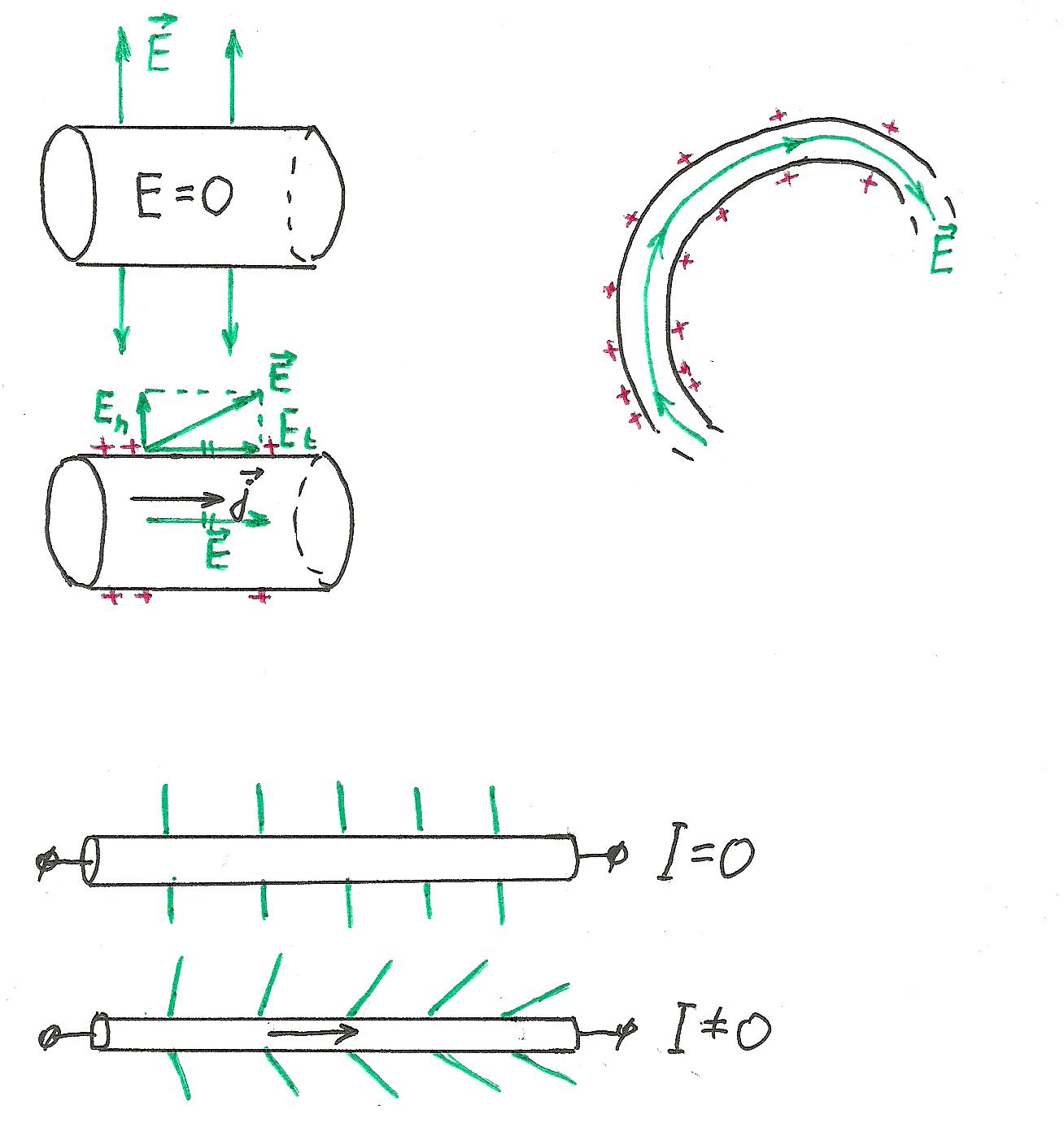
В электростатике было установлено, что
внутри металла
,
а вблизи его поверхности
поверхности.
Весь заряд распределяется только по
поверхности проводника.
Опыт показывает: чтобы в проводнике
(металле или электролите) тек ток, в нем
должно быть создано электрическое поле
,
причем плотность тока в каждой точке
пропорциональна
:
(1).
Для равномерного движения зарядов
требуется электрическая сила. Это
значит, что при движении по проводнику
зарядам приходится преодолевать
некоторое сопротивление. Скалярную
величину
называют удельной проводимостью
проводника (она зависит от рода металла
и от температуры). Обратная величина –
удельное сопротивление:
,
именно его обычно дают в таблицах (при
комнатной температуре).
Соотношение (1) называют законом Ома в дифференциальной форме, хотя точнее было бы назвать его законом в локальной форме, т.к. он связывает в каждой точке проводника две величины.