
- •Статистика
- •О.В. Рудакова,
- •Введение
- •Раздел 1 описательная статистика
- •Глава 1. Статистическое наблюдение
- •1.1. Основные понятия
- •1.2. Тест
- •1. Объект статистического наблюдения – это:
- •2. Субъект, от которого поступают данные в ходе статистического наблюдения, называется:
- •Глава 2. Статистическая сводка и группировка
- •2.1. Основные понятия
- •1) По формуле Стерджесса:
- •2100–9100 – 1-Я группа;
- •9100–16100 – 2-Я группа;
- •16100–23100 – 3-Я группа.
- •2.3.2 Задачи
- •Глава 3. Статистические показатели
- •3.1. Основные понятия
- •3.3.2 Задачи
- •Глава 4. Средние величины
- •4.1. Основные понятия
- •4.3.2 Задачи
- •Раздел 2 аналитическая статистика
- •Глава 5. Показатели вариации
- •5.1. Основные понятия
- •5.2. Тест
- •1. Вариация – это:
- •2. К абсолютным показателям вариации не относятся:
- •5.3.2 Задачи
- •Глава 6. Ряды динамики
- •6.1. Основные понятия
- •6.3.2. Задачи
- •Глава 7. Экономические индексы
- •7.1. Основные понятия
- •7.3.2. Задачи
- •Глава 8. Выборочное наблюдение
- •8.1. Основные понятия
- •8.3.2. Задачи
- •Глава 9. Статистическое изучение взаимосвязи социально-экономических явлений
- •9.1. Основные понятия
- •9.3.2. Задачи
- •Раздел 3 социально-экономическая статистика
- •Глава 10. Статистика национального богатства. Статистика основных фондов
- •10.1. Основные понятия
- •С точки зрения накопленного капитала национальное богатство включает:
- •5. Какими показателями может характеризоваться наличие основных фондов?
- •6. Какие виды оценки основных фондов используются в практике учета и статистики?
- •7. Как определяется показатель фондоотдачи основных фондов?
- •8. Как определяется показатель фондовооруженности?
- •Глава 11. Статистика цен
- •11.1. Основные понятия
- •11.3 Задачи
- •Глава 12. Статистика населения
- •12.1. Основные понятия
- •12.3.2 Задачи
- •Глава 13. Статистика рынка труда
- •13.1. Основные понятия
- •Глава 14. Статистика уровня жизни населения
- •14.1. Основные понятия
- •Заключение
- •Литература
Глава 8. Выборочное наблюдение
8.1. Основные понятия
Выборочное наблюдение – несплошное наблюдение, при котором статистическому обследованию подвергаются единицы изучаемой совокупности, отобранные случайным способом.
Выборочная совокупность – совокупность отобранных для обследования единиц.
Генеральная совокупность – совокупность единиц, из которых производится отбор.
В процессе проведения выборочного наблюдения, как и вообще при анализе данных любого обследования, возможны ошибки. Расчет ошибок позволяет решить одну из главных задач выборочного наблюдения - оценить репрезентативность (представительность) выборочной совокупности. Различают среднюю и предельную ошибки выборки. Эти два вида ошибок связаны следующим соотношением:
![]() ,
,
где ![]() – предельная ошибка выборки;
– предельная ошибка выборки;
![]() – средняя
ошибка выборки;
– средняя
ошибка выборки;
![]() – коэффициент
доверия, определяемый в зависимости от
уровня вероятности.
– коэффициент
доверия, определяемый в зависимости от
уровня вероятности.
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки. При проведении выборочного наблюдения используют следующие способы отбора:
собственно случайный отбор – отбор единиц производится из всей совокупности непреднамеренно (случайно);
механический отбор – разновидность случайного отбора, при котором отбор единиц производится механически, т.е. через определенный интервал;
типический отбор – отбор, при котором неоднородная генеральная совокупность предварительно разбивается на однородные (типические) группы, из которых случайно производят отбор необходимой численности выборки;
серийный отбор – это отбор не отдельных единиц, а их групп, осуществляемый для того, чтобы в таких группах подвергались наблюдению все единицы без исключения.
Различают бесповторный и повторный отбор.
При повторном отборе каждая единица совокупности может участвовать в выборке несколько раз, при бесповторном – это исключено.
При случайном повторном отборе средняя ошибка определяется по формуле:
![]()
при бесповторном:
![]()
где – выборочная (или генеральная) дисперсия;
![]() – выборочное (или
генеральное) среднее квадратическое
отклонение;
– выборочное (или
генеральное) среднее квадратическое
отклонение;
n – объем выборочной совокупности;
N – объем генеральной совокупности.
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:
![]()
где
![]() и
и
![]() –
генеральная и выборочная средние
соответственно;
–
генеральная и выборочная средние
соответственно;
![]() –
предельная ошибка
выборочной средней.
–
предельная ошибка
выборочной средней.
Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака. В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется по формуле:
![]()
где ![]() – доля единиц, обладающих данным
признаком в выборочной совокупности,
определяемая как отношение количества
соответствующих единиц к объему выборки.
– доля единиц, обладающих данным
признаком в выборочной совокупности,
определяемая как отношение количества
соответствующих единиц к объему выборки.
Тогда при собственно случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:
![]()
Соответственно при бесповторном отборе:

Пределы доли признака в генеральной совокупности р выглядят следующим образом:
![]() .
.
Ошибки
и пределы генеральных характеристик
при других способах формирования
выборочной совокупности определяются
на основе соответствующих формул,
отражающих особенности этих видов
выборки. Например, в случае типической
выборки
показателем вариации является средняя
из внутригрупповых дисперсий –
![]() ,
при серийной
выборке –
межгрупповая дисперсия
,
при серийной
выборке –
межгрупповая дисперсия
![]() и т.д. Кроме того, в последнем случае
вместо объема выборочной совокупности
n
используется показатель серий r.
и т.д. Кроме того, в последнем случае
вместо объема выборочной совокупности
n
используется показатель серий r.
Следовательно, для типической выборки средняя ошибка вычисляется по формулам:
при отборе, пропорциональном объему типических групп:
![]() (повторный отбор);
(повторный отбор);
 (бесповторный отбор);
(бесповторный отбор);
при отборе, пропорциональном вариации признака (не пропорциональных объему групп):
 (повторный отбор);
(повторный отбор);
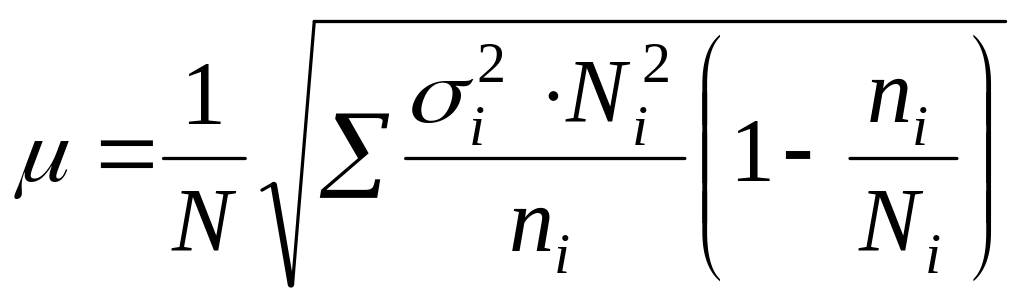 (бесповторный
отбор),
(бесповторный
отбор),
где ![]() и
– объемы i-й
типической группы и выборки из нее
соответственно;
и
– объемы i-й
типической группы и выборки из нее
соответственно;
![]() – групповые
дисперсии.
– групповые
дисперсии.
При серийной выборке средняя ошибка определяется следующим образом:
![]() (повторный отбор);
(повторный отбор);
![]() (бесповторный
отбор),
(бесповторный
отбор),
где ![]() – число серий в генеральной совокупности;
– число серий в генеральной совокупности;
![]() – межгрупповая
(межсерийная) дисперсия;
– межгрупповая
(межсерийная) дисперсия;
![]() – число серий в
выборочной совокупности.
– число серий в
выборочной совокупности.
Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки.
На практике наиболее часто применяют следующие выражения необходимого объема выборки:
собственно случайная и механическая выборка:
![]() (повторный отбор);
(повторный отбор);
![]() (бесповторный
отбор);
(бесповторный
отбор);
типическая выборка:
![]() (повторный отбор);
(повторный отбор);
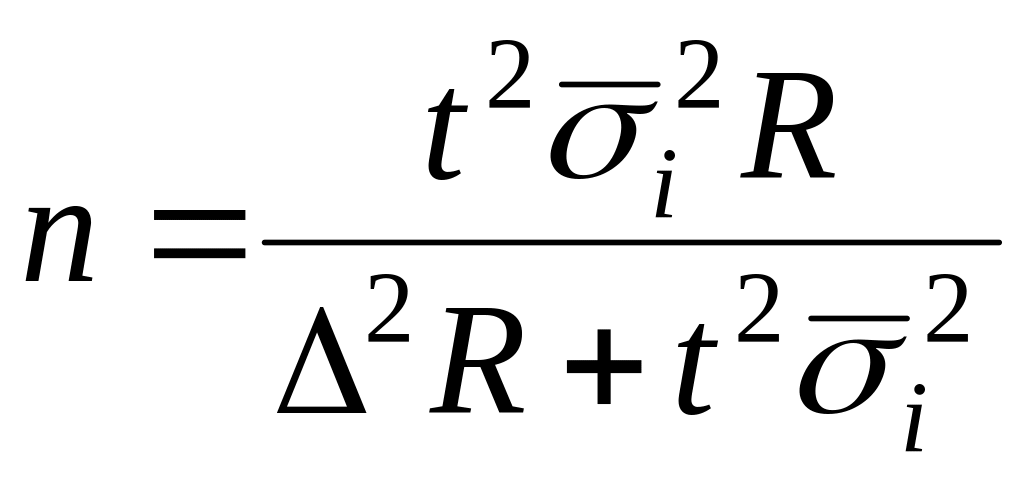 (бесповторный
отбор);
(бесповторный
отбор);
серийная выборка:
![]() (повторный отбор);
(повторный отбор);
![]() (бесповторный
отбор).
(бесповторный
отбор).
8.2. Тест
Выберите правильный ответ:
1. Выборочная совокупность – это:
а) совокупность отобранных для обследования единиц;
б) совокупность единиц, из которых производится отбор.
2. Типический отбор:
а) когда отбор единиц производится из всей совокупности непреднамеренно;
б) отбор, при котором неоднородная генеральная совокупность предварительно разбивается на однородные группы, из которых случайно производится отбор необходимой численности выборки;
в) отбор не отдельных единиц, а их групп.
3. При проведении выборочного наблюдения используются следующие методы:
а) повторный отбор;
б) индивидуальный отбор;
в) серийный отбор;
г) бесповторный отбор.
4. Величина предельной ошибки выборки зависит от:
а) колеблемости признака;
б) численности выборки;
в) доверительной вероятности;
г) метода отбора;
д) а, в, г;
е) а, б, в, г;
ж) б, г.
5. Способ отбора должен удовлетворять следующим требованиям:
а) обеспечение любой единице совокупности равных возможностей попасть в выборку;
б) необходимо формировать выборочную совокупность из достаточного количества единиц совокупности;
в) а, б.
6. Чтобы уменьшить ошибку выборки, рассчитанную в условиях механического отбора, нужно:
а) уменьшить численность выборочной совокупности;
б) увеличить численность выборочной совокупности.
7. Средняя из групповых дисперсий в генеральной совокупности составляет 64% общей дисперсии. Средняя ошибка выборки при механическом отборе из этой совокупности будет при одном и том же объеме выборки больше типической выборки на:
а) 36%;
б) 64%;
в) 25%;
г) предсказать результат невозможно.
8. Средняя ошибка выборки зависит от:
а) колеблемости признака в генеральной совокупности;
б) числа отобранных единиц;
в) а, б;
г) способа производства выборки;
д) а, б, г.
9. По данным 10%-ного выборочного обследования, дисперсия средней заработной платы сотрудников первого туристического агентства 225, а второго – 100. Численность сотрудников первого туристического агентства в 4 раза больше, чем второго. Ошибка выборки больше:
а) в первом туристическом агентстве;
б) во втором туристическом агентстве;
в) ошибки одинаковы;
г) предсказать результат невозможно.
10. Повторный отбор дает более точные результаты по сравнению с бесповторным:
а) верно; |
б) неверно |
8.3. Задачи
8.3.1 Примеры решения задач
Пример 1. При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделий в генеральной совокупности.
Решение: сначала
рассчитаем предельную ошибку выборки.
Так, при
![]() .
При случайном повторном отборе предельная
ошибка выборки определяется по формуле:
.
При случайном повторном отборе предельная
ошибка выборки определяется по формуле:
![]()
Определим пределы генеральной средней:
![]() .
.
30
– 0,84
![]() 30 +0,84, или 29,16
30,84.
30 +0,84, или 29,16
30,84.
Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 до 30,84 г.
Пример 2. В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2 %-я случайная бесповторная выборка семей. По её результатам было получено следующее распределение семей по числу детей (табл. 8.1).
Таблица 8.1 – Распределение семей по числу детей в городе в 2010 г.
Число детей в семье, чел. |
Количество детей, чел. |
0 |
1000 |
1 |
2000 |
2 |
1200 |
3 |
400 |
4 |
200 |
5 |
200 |
С вероятностью 0,954 найдите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение: вначале на основе имеющегося распределения семей определим выборочную среднюю и дисперсию. Для удобства расчет оформим в виде таблицы 8.2.
Таблица 8.2 – Вспомогательные расчеты для определения дисперсии и выборочной средней
Число детей в семье |
Количество семей |
|
|
|
|
0 |
1000 |
0 |
-1,5 |
2,25 |
2250 |
1 |
2000 |
2000 |
-0,5 |
0,25 |
500 |
2 |
1200 |
2400 |
0,5 |
0,25 |
300 |
3 |
400 |
1200 |
1,5 |
2,25 |
900 |
4 |
200 |
800 |
2,5 |
6,25 |
1250 |
5 |
200 |
1000 |
3,5 |
12,25 |
2450 |
Итого: |
5000 |
7400 |
– |
– |
7650 |
![]() чел.;
чел.;
![]()
Вычислим теперь предельную ошибку выборки (с учетом того, что p = 0,954 и t = 2). Для случайной бесповторной выборки предельная ошибка вычисляется по формуле:
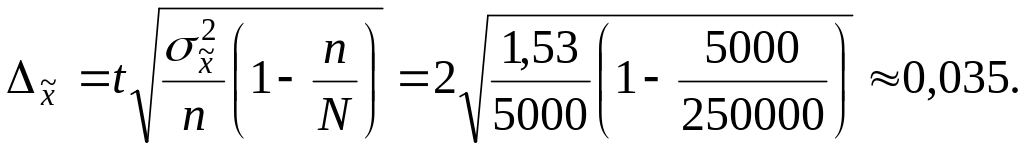
Следовательно, пределы генеральной средней:
![]()
Таким образом, с вероятностью 0,954 можно утверждать, что в среднем на каждые две семьи приходятся три ребенка.
Пример 3. С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. человек, в том числе 7 тыс. мужчин и 5 тыс. женщин.
На основании предыдущих обследований было известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 (t = 3) и ошибке 5 %.
Решение: рассчитаем общую численность типической бесповторной выборки:
 человек.
человек.
Вычислим объем отдельных типических групп:
![]() человек;
человек;
![]() человек.
человек.
Таким образом, необходимый объем выборочной совокупности сотрудников коммерческих банков составляет 550 человек, в том числе 321 мужчина и 229 женщина.
