5.2. Тест
Выберите правильный ответ.
1. Вариация – это:
а) изменение массовых явлений во времени;
б) изменение структуры статистической совокупности в пространстве;
в) изменение значений признака во времени и в пространстве;
г) изменение состава совокупности.
2. К абсолютным показателям вариации не относятся:
а) коэффициент вариации;
б) размах вариации;
в) дисперсия;
г) коэффициент осцилляции;
д) среднее квадратическое отклонение;
е) среднее линейное отклонение.
3. Коэффициент вариации рассчитывается по формуле:
а) |
б) |
в) |
|
|
|
;
;
;4. Если все значения признака уменьшить или увеличить на какое-то постоянное число, то дисперсия от этого не изменится:
а) неверно; |
б) верно. |
5. Показатель вариации, характеризующий долю усредненного значения абсолютных отклонений от средней величины, носит название:
а) коэффициент осцилляции;
б) относительное линейное отклонение;
в) коэффициент вариации.
6. Для расчета среднего квадратического отклонения (взвешенного) используется следующая формула:
а) |
б) |
в) |
;
;
.7. Если все значения признака уменьшить на 3, то величина дисперсии:
а) не изменится;
б) уменьшится на 3;
в) увеличится на 3;
г) уменьшится на 9;
д) увеличится на 9;
е) предсказать изменение дисперсии нельзя.
8. Межгрупповая дисперсия характеризует:
а) вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию;
б) систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под действием признака-фактора, положенного в основание группировки;
в) случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и независящую от признака-фактора.
9. Правило сложения дисперсий гласит:
а) общая дисперсия равна сумме межгрупповой дисперсии и внутригрупповых дисперсий;
б) общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсии, появляющейся под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.
10. Если отсутствуют различия между вариантами внутри групп, межгрупповая дисперсия равна:
а) единице;
б) нулю;
в) колеблется от нуля до единицы;
г) общей дисперсии;
д) средней из групповых дисперсий.
11. Разница между максимальным и минимальными значениями признака носит название:
а) среднее линейное отклонение;
б) размах вариации;
в) дисперсия.
5.3. Задачи
5.3.1 Примеры решения задач
Пример 1. На основе данных таблицы 5.1 (графы 1, 2) рассчитаем дисперсию и среднее квадратическое отклонение для интервального ряда распределения.
Таблица 5.1– Распределение магазинов города по товарообороту во 2-м квартале 2010 г.
Группы магазинов по величине товарооборота, тыс. руб. |
Число магазинов
|
Середина интервала, тыс. руб.,
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
60–70 |
3 |
65 |
195 |
2809 |
8427 |
70–80 |
5 |
75 |
875 |
1849 |
9245 |
80–90 |
7 |
85 |
595 |
1089 |
7623 |
90–100 |
10 |
95 |
950 |
529 |
5290 |
100–110 |
13 |
105 |
1365 |
169 |
2197 |
110–120 |
22 |
115 |
2530 |
9 |
198 |
120–130 |
20 |
125 |
2500 |
49 |
980 |
130–140 |
12 |
135 |
1620 |
289 |
3468 |
140–150 |
5 |
145 |
725 |
729 |
3645 |
150–160 |
3 |
155 |
465 |
1369 |
4107 |
Итого: |
100 |
|
11820 |
|
45180 |
Решение:
При расчете показателей вариации по интервальным рядам распределения необходимо сначала определить середины интервалов, а затем вести дальнейшие расчеты, рассматривая ряд середин интервалов как дискретный вариационный ряд распределения.
Результаты вспомогательных расчетов для определения дисперсии и среднего квадратического отклонения содержатся в графах (3-6) таблицы 5.1.
Средний размер товарооборота определяется по средней арифметической взвешенной и составляет:
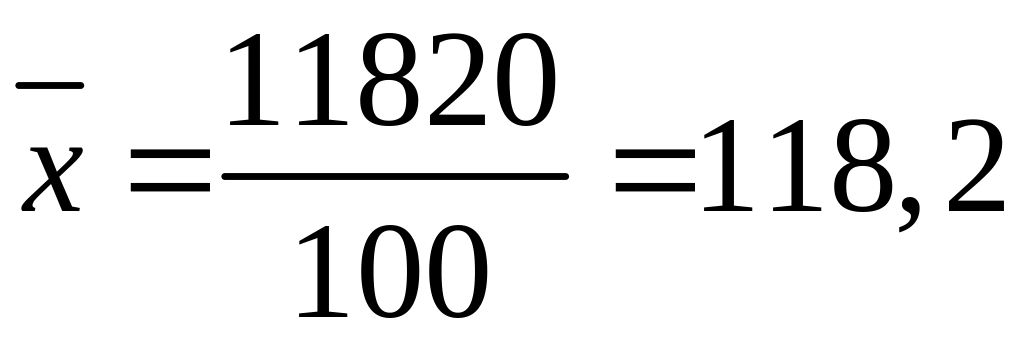тыс. руб.
Дисперсия товарооборота:
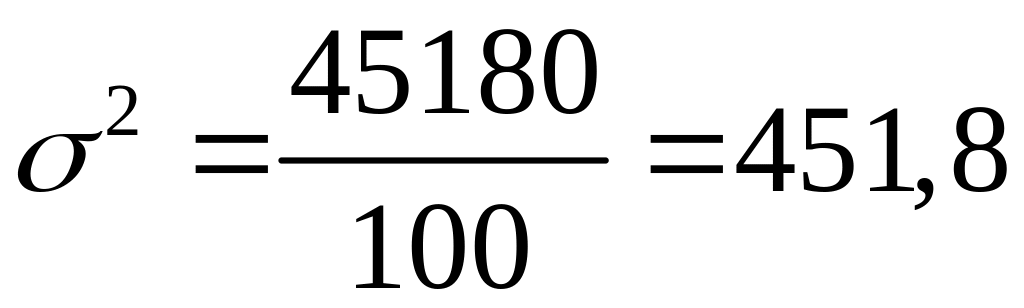тыс.
руб.
Среднее квадратическое отклонение товарооборота определяется как корень квадратный из дисперсии:
тыс.
руб.
Воспользуемся данными таблицы 5.1 и рассчитаем дисперсию по способу моментов и способу отсчета от условного нуля (табл. 5.2).
Таблица 5.2 – Расчет дисперсии способом отсчета от условного нуля
Группы магазинов по величине товарооборота, тыс. руб. |
Число
магазинов,
|
Середина интервала, тыс. руб.
|
(А = 115) |
(k = 10) |
|
|
60–70 |
3 |
65 |
-50 |
-5 |
-15 |
75 |
70–80 |
5 |
75 |
-40 |
-4 |
-20 |
80 |
80–90 |
7 |
85 |
-30 |
-3 |
-21 |
63 |
90–100 |
10 |
95 |
-20 |
-2 |
-20 |
40 |
100–110 |
13 |
105 |
-10 |
-1 |
-13 |
13 |
110–120 |
22 |
115 |
0 |
0 |
0 |
0 |
120–130 |
20 |
125 |
10 |
1 |
20 |
20 |
130–140 |
12 |
135 |
20 |
2 |
24 |
48 |
140–150 |
5 |
145 |
30 |
3 |
15 |
45 |
150–160 |
3 |
155 |
40 |
4 |
12 |
48 |
Итого: |
100 |
|
|
|
-18 |
432 |
По способу отсчета от условного нуля:
По способу моментов получаем:
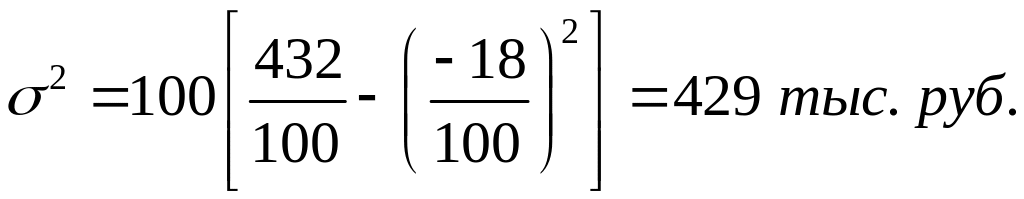
Разница в расчетах дисперсий получена в связи с округлением средней величины до целого числа. В идеале значения дисперсии, рассчитанной различными способами по одним и тем же данным, должны совпадать.
Пример 2. Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным табл. 5.3.
Таблица 5.3 – Производительность труда двух бригад
1-я бригада |
2-я бригада |
||||||
№ п/п |
Изготовлено деталей за
час, шт.,
|
|
|
№ п/п |
Изготовлено деталей за час, шт., |
|
|
1 |
13 |
-2 |
4 |
7 |
18 |
-3 |
9 |
2 |
14 |
-1 |
1 |
8 |
19 |
-2 |
4 |
3 |
15 |
0 |
0 |
9 |
22 |
1 |
1 |
4 |
17 |
2 |
4 |
10 |
20 |
-1 |
1 |
5 |
16 |
1 |
1 |
11 |
24 |
3 |
9 |
6 |
15 |
0 |
0 |
12 |
23 |
2 |
4 |
|
90 |
10 |
|
|
126 |
|
28 |
Решение: для расчета групповых дисперсий вычислим среднее по каждой группе:
шт.;
шт.
Промежуточные расчеты дисперсий по группам представлены в табл. 5.3. Подставив полученные значения в формулу, получим:
;
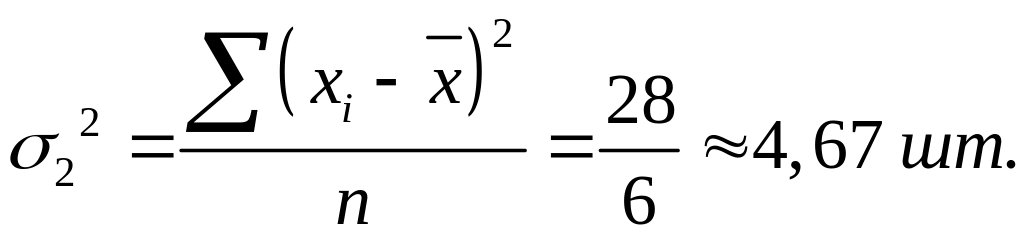
Средняя из групповых дисперсий:
Для расчета межгрупповой дисперсии определяем общую среднюю как среднюю взвешенную из групповых дисперсий:
шт.
Межгрупповая дисперсия:
Таким образом, общая дисперсия по правилу сложения дисперсий равна:
Проверим полученный результат:
