Глава 4. Средние величины
4.1. Основные понятия
Средний показатель – это показатель в форме средней величины, представляющий собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Средняя величина – это обобщающая мера варьирующего признака, которая характеризует ее уровень в расчете на единицу совокупности. Условиями применения средних величин являются наличие качественно однородной совокупности и достаточно большой объем выборки.
Средняя величина считается наиболее ценной и универсальной формой выражения статистических показателей. Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:
.
В каждом конкретном случае для реализации исходного соотношения требуется одна из форм средней величины. В статистической практике используют несколько видов средних величин: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая и т.д. Каждая из указанных средних может приобретать две формы: простую и взвешенную. Если среднюю вычисляют по первичным (несгруппированным) данным, применяют простую форму, если по вторичным (сгруппированным) – взвешенную.
Средняя арифметическая является наиболее распространенной средней. Средняя арифметическая простая применяется, когда значение вариантов встречается один раз:
,
где
–
i-й
вариант усредняемого признака;
– объем совокупности.
Средняя арифметическая взвешенная применяется, когда отдельное значение признака повторяется неодинаковое количество раз, т.е. она используется в расчетах средней по сгруппированным данным или вариационным рядам:
,
где
– вес i-го
варианта.
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений переходят от интервалов к их серединам.
Средняя арифметическая обладает некоторыми математическими свойствами, которые более полно раскрывают ее сущность и в ряде случаев используются при ее расчетах:
1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:
.
2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:
3. Если все осредняемые варианты уменьшить (увеличить) на постоянное число А, то средняя арифметическая уменьшится (увеличится) на ту же величину:
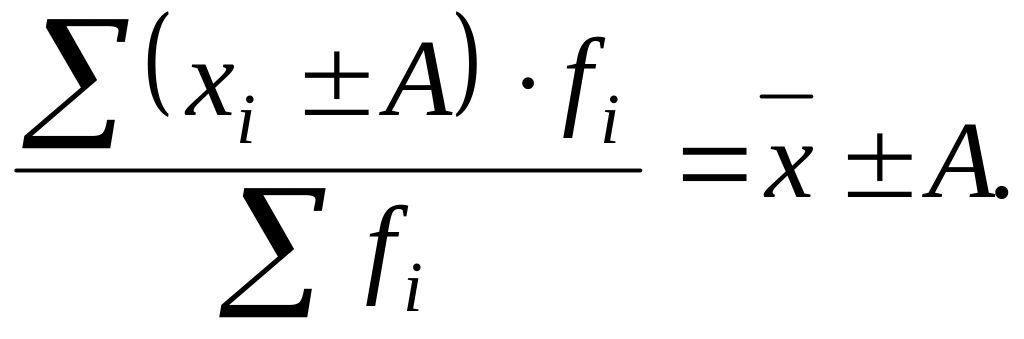
4. Если все варианты значений признака уменьшить (увеличить) в А раз, то средняя также уменьшится (увеличится) в А раз:
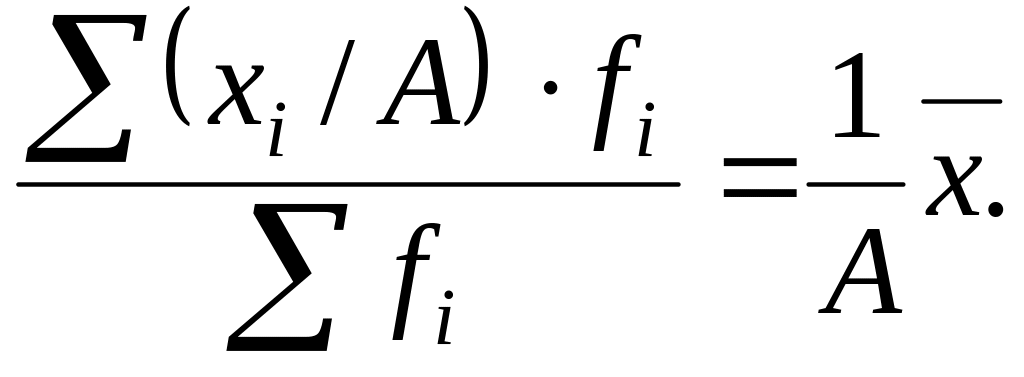
5. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:
.
Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной:
,
где
Когда
объемы явлений, т.е. произведения (
),
по каждому признаку равны, применяется
средняя
гармоническая простая:
.
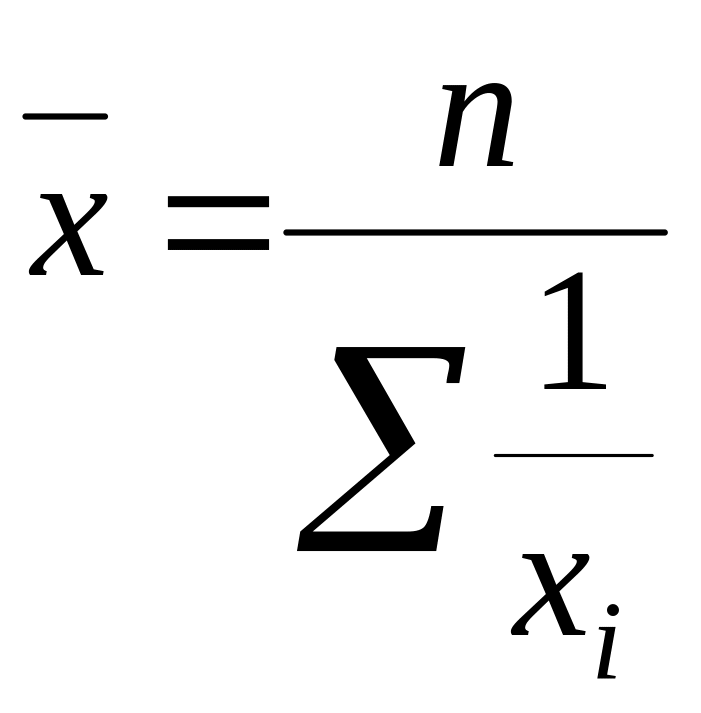Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии. Средняя геометрическая используется в расчетах среднегодовых темпов роста и для определения равноудаленной величины от минимального и максимального признака.
Средняя геометрическая простая вычисляется по формуле:
.
Средняя геометрическая взвешенная равна:
.
В качестве статистических характеристик вариационных рядов распределения рассчитываются так называемые структурные средние – мода и медиана.
Мода – значение признака, наиболее часто встречающее в исследуемой совокупности.
Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Вычисление медианы в дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечетное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда.
Для интервальных вариационных рядов мода определяется по формуле:
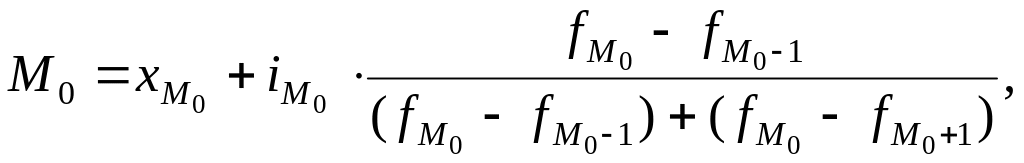
где 
– нижняя
граница значения интервала, содержащего
моду;
– величина
модального интервала;
– частота модального
интервала;
– частота интервала,
предшествующего модальному;
– частота интервала,
следующего за модальным.
Медиана интервального ряда распределения определяется по формуле:
где 
– нижняя
граница значения интервала, содержащего
медиану;
– величина
медианного интервала;
– сумма частот;
– сумма накопленных
частот, предшествующих медианному
интервалу;
– частота медианного
интервала.
4.2. Тест
Выберите правильный ответ.
1. Средняя величина – это:
а) значение признака, находящееся в середине ряда распределения;
б) обобщенная типическая характеристика признака в данной совокупности;
в) значение признака, встречающееся чаще других.
2. Для расчета средней величины по несгруппированным данным в случае возможности их прямого суммирования следует применять формулу:
а) арифметической простой;
б) арифметической взвешенной;
в) гармонической простой;
г) гармонической взвешенной.
3. Для расчета общей средней по сгруппированным данным следует применить формулу средней:
а) арифметической простой;
б) арифметической взвешенной;
в) гармонической простой;
г) гармонической взвешенной.
4. Для определения общей средней из коэффициентов выполнения плана по показателю по нескольким предприятиям следует применить формулу средней:
а) арифметической простой;
б) арифметической взвешенной;
в) гармонической простой;
г) гармонической взвешенной.
5. Возможна ли многовариантность значений среднего показателя, рассчитанного по одним и тем же данным?
а) да; |
б) нет. |
6. По какой формуле можно рассчитать среднюю арифметическую величину, если повторяемость каждого варианта признака равная?
а) средней арифметической простой;
б) средней арифметической взвешенной;
в) по обеим формулам.
7. Какую формулу средней следует использовать для определения процента выполнения плана по объединению (из двух предприятий), если первое предприятие выпустило продукции на сумму 800 тыс.рублей и выполнило план на 95 %, а второе произвело продукции на 900 тыс. рублей и выполнило план на 102 %?
а) простую среднюю арифметическую;
б) взвешенную среднюю арифметическую;
в) взвешенную среднюю гармоническую.
8. Для измерения вариации значения признака применяются следующие статистические показатели:
а) средние величины;
б) мода и медиана;
в) размах вариации, среднее линейное отклонение, дисперсия,
г) среднеквадратическое отклонение, коэффициент вариации.
9. Если все значения признака увеличить (уменьшить) на некоторую постоянную величину, то средняя арифметическая:
а) не изменится;
б) увеличится (уменьшится) на эту величину;
в) уменьшится (увеличится на эту величину.
10. Если все значения признака умножить (разделить) на некоторую постоянную величину, то средняя арифметическая:
а) не изменится;
б) увеличится (уменьшится) во столько раз;
в) уменьшится (увеличится) во столько раз.
4.3. Задачи
4.3.1 Примеры решения задач
Пример 1. По данным таблицы 4.1 рассчитаем среднюю заработную плату в целом по трем предприятиям.
Таблица 4.1 – Заработная плата на предприятиях АО в 2011 г.
Предприятие |
Численность промышленно-производственного персонала, чел. |
Средняя заработная плата, тыс. руб. |
1 |
540 |
12,5 |
2 |
275 |
13,0 |
3 |
458 |
13,1 |
Итого: |
1273 |
? |
Определим исходное соотношение средней для показателя «Средняя заработная плата»:
Нам известен знаменатель исходного соотношения, но не известен числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на численность ППП. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
тыс.
руб.
Допустим, что нам известны только данные о фонде заработной платы и средней заработной плате персонала (табл. 4.2), т.е. известен числитель исходного соотношения, но не известен его знаменатель.
Таблица 4.2 – Месячный фонд заработной платы и средняя заработная плата на предприятиях АО в 2011 г.
Предприятие |
Месячный фонд заработной платы, тыс. руб. |
Средняя заработная плата, тыс. руб. |
1 |
6750,0 |
12,5 |
2 |
3575,0 |
13,0 |
3 |
5999,8 |
13,1 |
Итого |
16324,8 |
? |
Численность работников по каждому предприятию можно получить делением фонда заработной платы на среднюю заработную плату. Тогда для расчета средней заработной платы мы будем использовать формулу средней гармонической взвешенной:
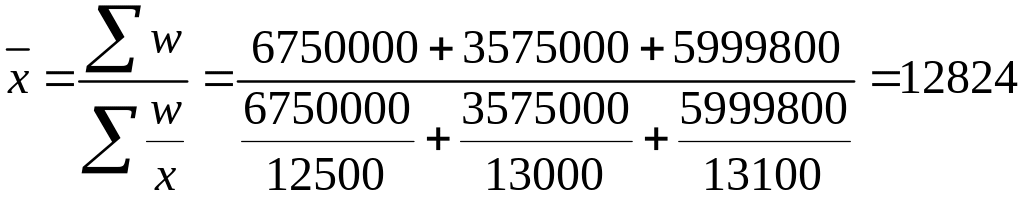руб.
Пример 2. По данным таблицы 4.3 определим величину среднедушевого дохода по городу.
Таблица 4.3 – Распределение населения города в 1-м квартале 2009 г. по уровню среднедушевых денежных доходов
Среднедушевой денежный доход в среднем за месяц, руб. |
Численность населения, % к итогу |
До 5000 |
10,5 |
5000–5500 |
16,7 |
5500–6000 |
30,2 |
6000–6500 |
24,4 |
6500–7000 |
6,5 |
7000–8500 |
6,7 |
Свыше 8500 |
5,0 |
Итого |
100 |
.
Так как мы имеем интервальный ряд, то определяем середины интервалов. При этом величину первого интервала условно приравниваем к величине второго, а величину последнего интервала приравниваем к величине предпоследнего. В результате получаем следующие середины интервалов:
4750 |
5250 |
5750 |
6250 |
6750 |
7250 |
7750 |
Роль численности населения выполняет его доля в общем итоге, выраженная в процентах. Для расчета воспользуемся формулой средней арифметической взвешенной:
руб.
Пример 3. Рассчитаем моду и медиану по данным таблицы 4.4.
Таблица 4.4 – Распределение семей города по размеру
среднедушевого дохода в январе 2011 г.
Группы семей по размеру дохода, тыс. руб. |
Число семей |
Накопленные частоты |
До 5 |
600 |
600 |
5 – 8 |
700 |
1300 |
8 – 10 |
1700 |
3000 |
10 – 15 |
2500 |
5500 |
15 – 20 |
2200 |
7700 |
20 – 50 |
1500 |
9200 |
Свыше 50 |
800 |
10000 |
Итого: |
10000 |
|
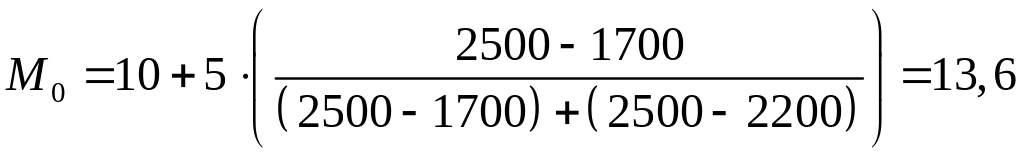тыс. руб.
Следовательно, наибольшее число семей в январе 2011 г. имели среднедушевой доход 13,6 тыс. рублей.
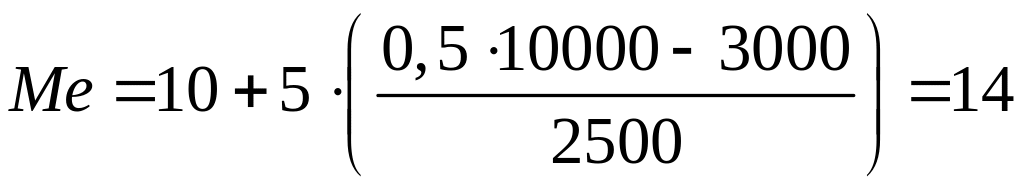тыс. руб.
Таким образом, половина семей города имели в январе 2011 г. среднедушевой доход менее 14 тыс. руб., остальные семьи – более 14 тыс. руб.