Глава 10. Основы цифровой электроники

10.1 Представление информации в цифровой системе

Основу построения современной вычислительной техники составляют так называемые цифровые схемы, реализующие различные арифметические и логические операции. В отличие от традиционной арифметики и логики в цифровых схемах оперируют двоичными представлениями цифр, чисел, логических функций и их аргументов. Инструментом для построения цифровых схем служит Булева алгебра, которая применительно к цифровой технике называется также алгеброй логики.

Двоичные представления переменных характеризуются тем, что они принимают только два значения, которые обычно называют нулем и единицей и обозначают символами 0 и 1 соответственно. Таким образом, для двоичной переменной X_i можно записать X_i = {0,1}. В алгебре логики существуют три основные операции:

- логическое умножение (конъюнкция) с обозначением y=x₁x₂=x₁x₂=x₁x₂;

- логическое сложение (дизъюнкция) с обозначением у = х₁ х₂ = х₁+х₂;

- инверсия с обозначением .

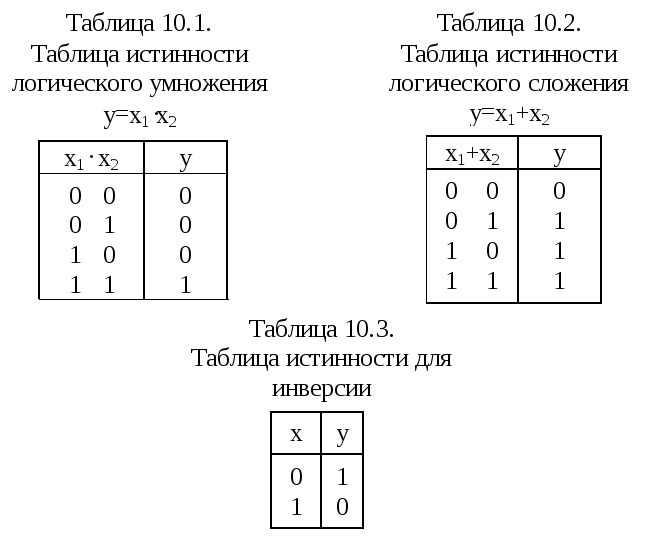
Правила определения значений логических функций удобно определять через так называемые таблицы истинности, в которых устанавливаются соответствия между двоичными значениями аргументов и функций.

Например, таблицы истинности 10.110.3 определяют значения логических функций умножения, сложения и инверсии для всех возможных значений переменных.

Аналогично можно определить результаты выполнения арифметических операций выполняемых при двоичном представлении чисел.

Например, в таблице 10.4 показано, как формируется результат сложения S двух двоичных чисел х₁ и х₂ с учетом переноса Р в старший разряд числа.

Таблица 10.4. Реализация операции двоичного сложения

Другим способом определения результатов логических и арифметических операций является их соответствующее аналитическое представление в виде формул, например в форме такого выражения:

y = х₁х₂х₃ + х₂х₄ + х₁х₂х₅ +…

Подробно с вопросами теории и практических применений булевой алгебры и двоичной арифметики, составляющих основу построения современных цифровых систем, можно ознакомиться в соответствующей литературе. Здесь мы подробнее остановимся на вопросах реализации электронных элементов и узлов, составляющих техническую основу построения цифровой техники.

Учитывая, что двоичные переменные имеют только два дискретных значения, в качестве соответствующих схемотехнических решений можно использовать схемы, имеющие два легко различимых рабочих состояния.

Простейшим способом реализации логической переменной, является обычный ключ, изображенный на рисунке 10.1.

Рис.10.1. Представление логической переменной в виде ключа

Можно условиться, что разомкнутый ключ эквивалентен логическому нулю, а замкнутый – логической единице. Легко убедится, что в этом случае два последовательно соединенных ключа будут реализовывать логическую функцию И, а два параллельно соединенных ключа – логическую функцию ИЛИ.

Другой возможностью представления логических переменных, которая и используется в современной цифровой технике, является электрическое напряжение, имеющее два хорошо различимых уровня: высокий и низкий, так как это реализовано, например, в транзисторных ключевых схемах, рассмотренных в предыдущем разделе.

Этим уровням ставятся в соответствие двоичные переменные ноль и единица (0, 1). При этом при использовании положительной логики логическому нулю ставится в соответствие низкий уровень напряжений, а логической единице – высокий. При использовании отрицательной логики применяется противоположный способ задания нуля и единицы.

Основные логические функции, их модификации и комбинации, а так же арифметические операции реализуются через соответствующие наборы стандартных электронных схем. При этом для реализации одной и той же функции существует и используется достаточно большое число различных электронных схем. Поэтому с целью упрощения документации, решения задач анализа и синтеза цифровых схем используют специальные условные изображения цифровых элементов, которые обозначают только выполняемую логическую функцию, но не раскрывают внутреннее строение схемы.

На рис.10.2 показан общий принцип обозначения элементов, каждый из которых состоит из прямоугольного поля, в котором размещается указатель функции выполняемой логическим элементом (*). Справа от поля логического элемента обычно указываются его выходы, слева – входы.

Рис.10.2. Общий принцип обозначения логических элементов

На рис. 10.3 показаны варианты изображения элементов, реализующих конкретные наборы логических функций.

Рис.10.3. Варианты изображений логических элементов

Поскольку в цифровой технике напряжение как физическая величина рассматривается редко, (в основном при проектировании схем элементов и при решении вопросов согласования) входные и выходные сигналы обозначаются символами U только при необходимости, а в основном они описываются обозначением логических переменных x, y, z и т.д.