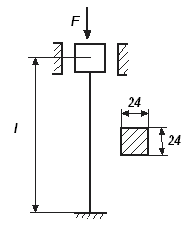
Практическая работа № 6 Расчет на устойчивость сжатых стержней

Цель работы: усвоение методики расчета на устойчивость сжатого стержня, определение

размеров сечения, критической силы и коэффициента запаса устойчивости

Задание: Проверить на устойчивость при 2<[s_y] <4 (отклонения от заданных значений [s_y] допускается в пределах ±10%) сжатую стальную стойку (рис.6.1), при необходимости подобрать размеры поперечного сечения стойки, удовлетворяющие этому условию. Данные для своего варианта взять из табл.6.1

Теоретическое обоснование

Некоторые элементы конструкции, называемые стержнями, длина кото­рых гораздо больше их поперечных размеров, под действием сжимающих сил испытывают деформацию продольного изгиба.

Продольным изгибом называется деформация стержня большой длины от сжимающей нагрузки в результате потери жесткости или потери упругости.

Нагрузка, при которой стержень теряет устойчивость, называется крити­ческой силой. Она определяется по формуле Эйлера:

где Е — модуль упругости первого рода (модуль Юнга);

J_min — минимальный осевой момент инерции сечения;

μ — коэффициент приведения длины, который характеризует за­висимость

критической силы от способа закрепления концов стержня (рис. 1.14);

l — длина стержня.

Рисунок 6.1

Минимальный осевой момент инерции сечения I_min определяется по фор­мулам:

• для круга

J_X =J_Y =πd⁴ /64≈0.05d⁴, мм⁴

• для кольца

J_X =J_Y = 0,05 d⁴ _н (1-α⁴),

где α = d_вн /d_н;

• для прямоугольника

J_X =bh³ /12, J_Y =hb³ /12.

• для стандартных профилей сортового проката I_min определяет по соответствующим таблицам сортамента

Для того чтобы стержень сохранял устойчивую форму равновесия, вели­чина сжимающей силы должна быть меньше критической: F_сж < F_кр.

Величина, которая показывает, во сколько раз сжимающая сила должна быть меньше критической силы, называется рабочим коэффициентом устой­чивости:

s_y = F_кр / F_сж.

Условие устойчивости сжатых стержней: рабочий коэффициент устойчи­вости должен быть больше или равен допускаемому коэффициенту устойчи­вости, т.е.

Допускаемый коэффициент устойчивости [n_у] задает конструктор, учитывая при этом материал и способы закрепления концов стрежня, режим его работы и характер нагрузок.

Под действием критической силы в поперечных сечениях стержня возникает критическое напряжение, которое определяется по формуле

где i = - радиус инерции сечения;

λ = - геометрическая гибкость стержня.

Вторая форма условия устойчивости: критическое напряжение должно быть меньше или равно пределу пропорциональности, т.е.

где σ_пц — предел пропорциональности, который характеризует упругие свойства

материала, подчиняющиеся закону Гука.

Формула Эйлера справедлива только для стержней большой гибкости, т.е. для стержней, у которых геометрическая гибкость больше или равна пре­дельной гибкости:

где λ_пр — предельная гибкость, величина которой определена опытным путем для

различных материалов (для стали λ_пр = 100; для чугу­на λ_пр =80).

Порядок выполнения работы

1. Определить предельную гибкость материала стойки

2. Определить основные геометрические характеристики сечения

3. Найти действительную гибкость стойки

4. Проверить применимость формулы Эйлера

5. Определить значение критической силы

6. Найти действительный коэффициент запаса устойчивости

7. Скорректировать размеры сечения при превышении запаса устойчивости

Контрольные вопросы

1. Дать определение критической силы?

2. В чем заключается явление потери устойчивости?

3. По каким формулам определяется величина критической силы?

4. В каких пределах применима формула Эйлера?

5. Почему в формуле Эйлера используется минимальный момент инерции сечения?

6. Что называется гибкостью стержня?

7. Что называется предельной гибкостью, от чего она зависит?

8. От чего зависит коэффициент приведения длины?

9. Как определяется критическое напряжение для стержней малой и средней гибкости?

10. Какой вид имеет график критических напряжений?

11. Как подбирают сечение стержня при расчете на устойчивость?

12. Как выбирается допускаемое напряжение для сжатых элементов при расчете строительных конструкций?

13. От чего зависит значение коэффициента снижения допускаемых напряжений?

14. Как найти изгибающий момент и прогиб при продольно-поперечном изгибе?

Пример выполнения

Проверить на устойчивость при 2<[s_y] <4 (отклонения от заданных значений [s_y] допускается в пределах ±10% ) сжатую стальную стойку (рис.6.1), при необходимости подобрать размеры поперечного сечения стойки, удовлетворяющие этому условию.

Дано: F =12 кН, l =2м, Е =2·10⁵ МПа, σ_пц =230 МПа.

Решение.

1. Определяем предельную гибкость материала стойки

2. Определяем основные геометрические характеристики сечения: площадь – А, минимальный момент инерции сечения – I_min, минимальный радиус инерции сечения -i_min.

А = a² = 24·24 = 576 мм²

I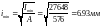 _min = a⁴ /12 = 24⁴ /12 = 27648 мм⁴

3. Находим действительную гибкость стойки

λ = η·l /i_min = 0.5·2000 /6.93 =144

где η =0,5

4. Проверяем применимость формулы Эйлера

λ ≥ λ_пред

λ = 144 > λ_пред = 92,5

Формула Эйлера применима

5. Определяем значение критической силы

6. Находим действительный коэффициент запаса устойчивости

s_y = F_кр / F = 54,52 /12 = 4,54

Отклонение от заданных значений [s_y]

Рис. 6.2

что больше допускаемого максимального значения, следовательно, необходимо принять меньшие размеры поперечного сечения и произвести расчет для принятых размеров.

Принимаем a =22мм

А = a²= 22·22 = 484 мм²

I_min = a⁴ /12 = 22⁴ /12 = 19521 мм⁴

λ = η·l /i_min = 0.5·2000 /6.35 = 158

λ=158 >λ_пред =92,5

s_y =F_кр / F =38,493/12 = 3,21

2< [s_y] = 3,21 <4

Заданное условие на устойчивость выполняется.

Таблица 6.1

№ вар.	Расч. схема, рис.6.1	Схема сечения	Сила F,кН	Длина l, м	№ вар.	Расч. схема, рис.6.1	Схема сечения	Сила F,кН	Длина l, м
1	а		60	1,8	21	в		76	3,1
2	б		65	2,0	22	г		74	3,4
3	в		70	2,2	23	в		72	3,5
4	г		75	2,4	24	б		70	3,2
5	в		80	2,6	25	а		68	2,9
6	б		85	2,8	26	б		66	2,6
7	а		90	3,0	27	в		64	2,3
8	б		95	3,2	28	г		62	2,0
9	в		100	3,4	29	в		60	1,7
10	г		98	3,3	30	б		63	1,8
11	в		96	3,1	31	а		73	1,9
12	б		94	2,9	32	б		83	2,0
13	а		92	2,7	33	в		93	2,1
14	б		90	2,5	34	г		89	2,2
15	в		88	2,3	35	в		87	2,3
16	г		86	2,1	36	б		85	2,4
17	в		84	1,9	37	а		83	2,5
18	б		82	2,2	38	б		81	2,6
19	а		80	2,3	39	в		79	2,7
20	б		78	2,8	40	г		77	2,8