Практическая работа № 5 Расчеты на прочность при изгибе
Цель работы: усвоение методики расчета на прочность при чистом изгибе
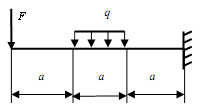
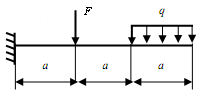
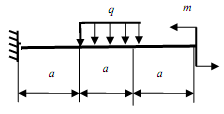
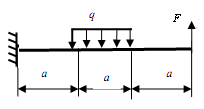
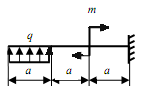
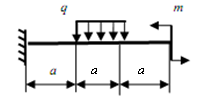
Задание: Для заданной консольной балки (рис.5.2, табл.5.1) подобрать размеры сечения прямоугольника с заданным отношением высоты и ширины: h/b = 2.
Для материала (сталь Ст3) принять допускаемое напряжение при изгибе: [σи] = 160 Н/мм2, Е = 2 · 105 МПа.
Теоретическое обоснование
Расчет балок на прочность обычно ведется по наибольшим нормальным напряжениям, возникающим в их поперечных сечениях. Обозначая эти напряжения σmax, получаем условие прочности в виде
σmax ≤ [σ]. (5.1)
где [σ] – допускаемое напряжение, зависящее в основном от материала балки и ее
назначения.
При расчете на прочность элементов конструкций, работающих на изгиб, возможны три вида задач, различающихся формой использования условия прочности (7.29):
а) проверка напряжений (проверочный расчет);
б) подбор сечения (проектный расчет);
в) определение допускаемой нагрузки (определение грузоподъемности).
Методика решения этих задач для балок из пластичных и хрупких материалов различна, так как балки из пластичных материалов одинаково работают на растяжение и сжатие, а из хрупких материалов лучше работают на сжатие, чем на растяжение. Это влияет на применяемые формы поперечных сечений балок и на способ определения опасного сечения.
Известные различия имеются также в расчетах балок постоянного по всей длине и переменного поперечного сечения.
Кроме того, следует иметь в виду, что в некоторых (сравнительно редких) случаях расчет на прочность только по наибольшим нормальным напряжениям, действующим в поперечном сечении балки, недостаточен, и приходится дополнительно производить проверку прочности также по главным напряжениям, возникающим в наклонных сечениях, и по максимальным касательным напряжениям.
Для реальной, закрепленной одним концом балки расчет целесообразно вести со свободного конца (чтобы избежать определения опорных реакций); в случае двухопорной балки решение задачи приходится начинать с определения опорных реакций.
Балки выполняют постоянного по длине поперечного сечения, поэтому его размеры подбирают только для опасного сечения – сечения с максимальным по абсолютному значению изгибающим моментом
Порядок выполнения работы
Вычертить в масштабе расчетную схему в соответствии со своими данными
Определить значение поперечных сил Q и изгибающих моментов M на каждом участке (построить эпюры Q и М).
Определить сечение, в котором значение изгибающего момента будет максимальным.
Из условия прочности подобрать величину поперечного сечения бруса.
Ответить на контрольные вопросы.
Контрольные вопросы
Какие внутренние силовые факторы возникают в поперечных сечениях балки при изгибе? Какое принято правило знаков при их определении?
Какие применяются основные правила проверки эпюр Q и M?
Как определяются нормальные напряжения в произвольной точке сечения и максимальные напряжения? Какой вид имеет эпюра нормальных напряжений в сечении?
Что такое осевой момент инерции сечения и момент сопротивления сечения при изгибе?
Чему равны моменты инерции и моменты сопротивления для прямоугольного, круглого и кольцевого сечений?
Каким образом определяют опасное сечение балки?
Как записывается условие прочности балки при изгибе? Какие задачи решаются на основе условия прочности?
Что понимается под рациональной формой сечения балки при изгибе? В чём преимущества применения балок стандартного профиля?
Какие перемещения рассматриваются при изгибе балок?
Пример выполнения
Для заданной консольной балки подобрать размеры сечения прямоугольника с заданным отношением
высоты и ширины. Для материала балки (сталь Ст.3) принять допускаемое напряжение при изгибе [σ] = 160Н/мм2. F1 = 20 kH, F2 = 20 kH, F3 = 44 kH, M = 16kH·м,
АВ = ВС = CD =0, 5 м.
Решение:
В заданном брусе три участка: 1, 2 и 3. Границами участков являются сечения, в которых приложены внешние силы и моменты. Так как силы и моменты, нагружающие брус, действуют в продольной плоскости, совпадающей с плоскостью симметрии бруса, то в поперечных сечениях возникает два внутренних силовых фактора – изгибающий момент; Мu и поперечная сила Q, т. е. брус испытывает изгиб.
Для определения изгибающего момента применяем метод сечений. Проводя мысленно сечение в пределах каждого из участков, будем отбрасывать правую закрепленную часть балки и оставлять для рассмотрения левую часть. Эпюру изгибающих моментов строим по характерным точкам, т. е вычисляем Ми в характерных сечениях А, В, Си В.
В сечении А изгибающий момент Миа=0, так как относительно, точки А внешняя сила F1 момента не создает (плечо силы равно нулю).
В сечении В изгибающий момент
MиВ = F1·AB = 20·0, 5 = 10 кН·м
В сечении С участка 2 (т. е. в сечении, бесконечно близком к сечению С слева) изгибающий момент
MиС2 = F1·AС – F2·ВС = 20·1 - 20·0, 5 = 10 кН·м
В селении С участка 3 (т. е. в сечении бесконечно близком к сечению С справа) изгибающий момент
MиС3 = F1·AС – F2·ВС -М = 20·1 - 20·0, 5 – 16 = -6 кН·м
(т.е. в сечении С изгибающий момент изменился скачками на значение приложенного здесь внешнего момента М).
В сечении D изгибающий момент
MиD = F1·AD – F2·ВD -М – F3·CD = 20·1,5 - 20·1 – 16 - 44·0,5 = -28 кН·м
Нанося полученные характерные точки на график и соединяя их прямыми линиями, получаем эпюру изгибающих моментов (рис, 5.1. 6).
Определяем размеры поперечного сечения балки, для чего используем условие прочности при изгибе
где Wх - осевой момент сопротивления,
Mи - максимальный изгибающий момент. В нашем случае опасное сечение (сечение D).
Сечение – прямоугольник с заданным отношением высоты и ширины. Для
прямоугольника момент сопротивления
Wx = bh2/6
В нашем случае
Wx = hh2/(1,5∙6) = h3/9
Приравнивая
h3/9 = 175 см3
находим
h = 11, 7 см, b = 7,8 см
Площадь прямоугольного сечения
A = bh = 7,8∙11,7 = 91,3см2
Mu = 28кН·м = 28·103·103Н·мм
σ = Mu/Wx ≤ [σ]
σ = 28·103·103/Wx ≤ 160
Условие прочности соблюдается
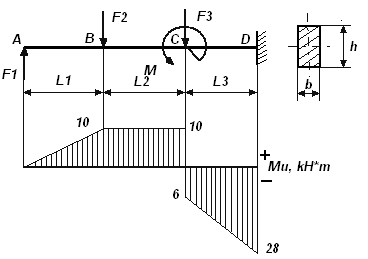
Рис.5.1
1
|
5 |
2
|
6 |
3
|
7 |
4
|
8
|
|
|
Типы сечений балок |
|
a
|
б |
Рис. 5.2 |
|
Таблица 5.1
№ варианта |
№ рис. |
q |
m |
F |
a |
Тип сечения |
1 |
1 |
3 |
2 |
1 |
0,2 |
а |
2 |
2 |
4 |
3 |
2 |
0,3 |
б |
3 |
3 |
5 |
4 |
3 |
0,4 |
а |
4 |
4 |
6 |
5 |
4 |
0,5 |
б |
5 |
5 |
7 |
6 |
5 |
0,6 |
а |
6 |
6 |
8 |
7 |
6 |
0,7 |
б |
7 |
7 |
9 |
8 |
7 |
0,8 |
а |
8 |
8 |
10 |
9 |
8 |
0,9 |
б |
9 |
1 |
15 |
10 |
9 |
1,0 |
а |
10 |
2 |
3 |
2 |
1 |
0,2 |
б |
11 |
3 |
4 |
3 |
2 |
0,3 |
а |
12 |
4 |
5 |
4 |
3 |
0,4 |
б |
13 |
5 |
6 |
5 |
4 |
0,5 |
а |
14 |
6 |
7 |
6 |
5 |
0,6 |
б |
14 |
7 |
8 |
7 |
6 |
0,7 |
а |
16 |
8 |
9 |
8 |
7 |
0,8 |
б |
17 |
1 |
10 |
9 |
8 |
0,9 |
а |
18 |
2 |
15 |
10 |
9 |
1,0 |
б |
19 |
3 |
3 |
2 |
1 |
0,2 |
а |
20 |
4 |
4 |
3 |
2 |
0,3 |
б |
21 |
5 |
5 |
4 |
3 |
0,4 |
а |
22 |
6 |
6 |
5 |
4 |
0,5 |
б |
23 |
7 |
7 |
6 |
5 |
0,6 |
а |
24 |
8 |
8 |
7 |
6 |
0,7 |
б |
25 |
1 |
9 |
8 |
7 |
0,8 |
а |
26 |
2 |
10 |
9 |
8 |
0,9 |
б |
27 |
3 |
15 |
10 |
9 |
1,0 |
а |
28 |
4 |
3 |
2 |
1 |
0,2 |
б |
29 |
5 |
4 |
3 |
2 |
0,3 |
а |
30 |
6 |
5 |
4 |
3 |
0,4 |
б |