
- •«Иркутский энергетический колледж» методические указания
- •140407 Электрические станции, сети и системы
- •140408 Релейная защита и автоматизации электроэнергетических систем
- •140101 Тепловые электрические станции
- •140407 Электрические станции, сети и системы
- •140408 Релейная защита и автоматизации электроэнергетических систем
- •Введение
- •Практическая работа № 1 Расчет статически определимых систем на растяжение и сжатие
- •Практическая работа № 2 Построение эпюр крутящих моментов и определение диаметра вала из условий прочности и жесткости при кручении
- •Практическая работа № 3 Расчеты на прочность и жесткость при кручении круглого бруса
- •Практическая работа № 4 Построение эпюр поперечных сил и изгибающих моментов
- •Практическая работа № 5 Расчеты на прочность при изгибе
- •Практическая работа № 6 Расчет на устойчивость сжатых стержней
- •Практическая работа № 8 Кинематический и силовой расчет многоступенчатой передачи
- •Практическая работа № 10 Составление кинематических схем приводов
- •Модели действующих приводов
- •Ориентировочные значения пределов прочности
- •Дополнительная
Практическая работа № 4 Построение эпюр поперечных сил и изгибающих моментов
Цель работы: научиться строить эпюры поперечных сил и изгибающих моментов
Задание: Для двухопорной балки построить эпюры поперечных сил и изгибающих моментов. Балка нагружена активными силами: сосредоточенной силой F и парой сил с моментом М. При расчете принять: [σ] = 160 МПа, F = 10 кН, M = 15 kH·м, l = 0,3 м.
Теоретическое обоснование
Чистым изгибом называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор - изгибающий момент Ми. В большинстве случаев одновременно с изгибающим моментом возникает и другой внутренний силовой фактор – поперечная сила Q; такой изгиб называют поперечным.
Изгибающий момент в произвольном поперечном сечении 6pуса численно равен алгебраической сумме моментов внешних сил, действующих на оставленную часть, относительно центра тяжести сечения:
Ми = ∑Мi (4.1)
Поперечная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, действующих на оставленную часть:
Q = ∑Fi (4.2)
Здесь имеется в виду, что все внешние силы и моменты действуют в главной продольной плоскости бруса, причем силы расположены перпендикулярно продольной оси.
При чистом изгибе в поперечных сечениях возникают нормальные напряжения, а при поперечном изгибе, кроме того, и касательные напряжения. Однако в подавляющем большинстве случаев влияние τ при расчете на прочность не учитывается, поэтому отпадает необходимость как в определении поперечных сил Q, так и в построении их эпюры.
 (4.3)
(4.3)
Установим следующее правило знаков для изгибающего момента: момент внешней силы или пары, изгибающий мысленно закрепленную в сечении оставленную часть бруса выпуклостью вниз, считается положительным (т. е. дает положительный изгибающий момент); в противном случае момент внешней силы или пары отрицателен (рис. 4).
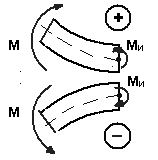
Рис.4.1
Для реальной, закрепленной одним концом балки расчет целесообразно вести со свободного конца (чтобы избежать определения опорных реакций); в случае двухопорной балки решение задачи приходится начинать с определения опорных реакций.
Балки выполняют постоянного по длине поперечного сечения, поэтому его размеры подбирают только для опасного сечения – сечения с максимальным по абсолютному значению изгибающим моментом
Порядок выполнения работы
Вычертить в масштабе расчетную схему в соответствии со своими данными.
Определить опорные реакции
Определить значение поперечных сил Q и изгибающих моментов M на каждом участке.
Построить эпюры Q и М.
Ответить на контрольные вопросы.
Контрольные вопросы
Что называется прямым изгибом?
Что называется чистым и поперечным изгибом?
Какие внутренние усилия возникают в поперечных сечениях бруса?
Какие правила знаков приняты для каждого из внутренних усилий?
Как вычисляются изгибающий момент и поперечная сила в поперечном сечении бруса?
Какая существует дифференциальная зависимость между изгибающим моментом,
поперечной силой и интенсивностью распределенной нагрузки?
Пример выполнения
Для двухопорной балки (рис.4.2) построить эпюры поперечных сил и изгибающих моментов. Балка нагружена активными силами: сосредоточенными силами F1 и F2 и парой сил с моментом М.
Дано:
F1 = 20 кН, F2 = 10 кН, AB = 2м, BC = 4м, CD = 2м, М = 2 кН

Рис.4.2
Решение:
Освободим балку от опор, заменив их опорными реакциями.
Составляем уравнение равновесия статики и определяем неизвестные реакции опор.

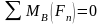




Проверяем правильность полученных результатов. Для этого проведем ось координат через одну из точек (ось Y) и спроецируем все силы на данную ось. Составим дополнительное уравнение ΣY = 0.
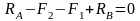
Подставим в уравнение полученные значения реакций RА и RВ.
17,75 – 20 – 10 + 12,25 = 0
Условие ΣY = 0 выполняется, следовательно, реакции опор найдены верно.
Делим балку (рис.4.3) на участки по характерным точкам А, В, С, D.
Определяем ординаты и строим эпюру Qу слева направо:

Вычисляем ординаты и строим эпюру Mи


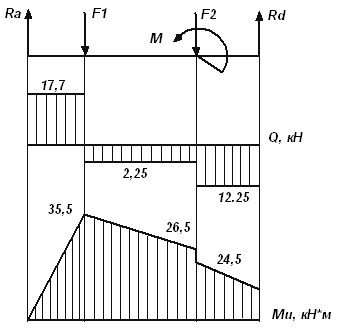
Рис. 4.3
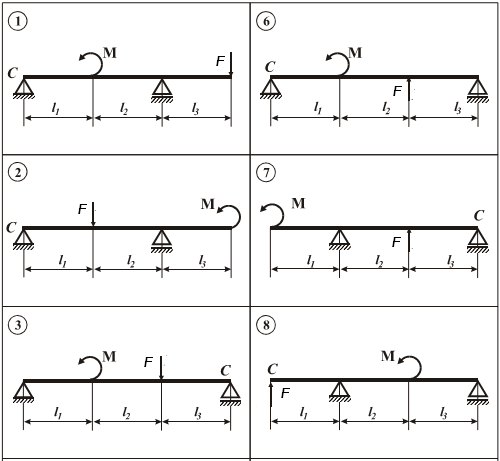

Рис. 4.4
Длины участков двухопорной балки
-
№ варианта
1
2
3
4
5
6
7
8
9
0
l1
2l
2,5l
2,5l
3l
3l
3l
2l
2,5l
2l
3l
l2
2,5l
3,5l
3l
2l
2,5l
3,5l
3,5l
4l
5l
4l
l3
3,5l
2l
2,5l
2,5l
2l
2l
2l
1,5l
2l
3l
