Практическая работа № 2 Построение эпюр крутящих моментов и определение диаметра вала из условий прочности и жесткости при кручении

Цель работы - научиться строить эпюры крутящих моментов для круглого вала, и

находить диаметр вала из условий прочности и жесткости.

Задание: Для стального вала круглого поперечного сечения определить значения

внешних моментов, соответствующих передаваемым мощ­ностям, и уравновешенный

момент (рис.2.7, табл.2.1). Построить эпюру крутящих моментов по длине вала.

Определить диаметры вала по сечениям из расчетов на проч­ность и жесткость.

Полученный больший результат округлить до ближайшего четного или

оканчивающегося на 5 числа. При расчете использовать следующие данные: вал

вращается с угловой скоростью ω = 25 рад/с; материал вала — сталь, [τ_k] = 30 МПа,

модуль упругости при сдвиге G = 8 • 10⁴ МПа; допускаемый угол закручивания

[ ] = 0,02 рад/м. Провести расчет для вала кольцевого сечения, приняв с = 0,9. Сделать

выводы о целесообразности выполнения вала круглого или кольцевого сечения, сравнив

площади поперечных сечений.

Теоретическое обоснование

Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор – крутящий момент. Внешними нагрузками также являются две противоположно направленные пары сил. Стержни круглого или кольцевого сечения, работающие на кручение, называют валами. При расчете валов обычно бывает, известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

Пусть вал вращается с постоянной скоростью ω рад/с. и передает мощность Р кВт. Угловая скорость вращения вала равна (рад/сек), а передаваемая мощность

Р = М·ω. (2.1)

Вращающий момент равен

М =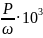 , Н·м (2.2)

Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала. Крутящий момент Мк в сечении вала численно, равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала.

Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость.

Примем правило знаков для крутящего момента: его положительное направление соответствует повороту сечения по ходу часовой стрелки, если смотреть на сечение со стороны внешней нормали (рис. 2.1).

Рис 2.1

В поперечных сечениях бруса при кручении возникают касательные напряжения, направление которых в каждой точке перпендикулярно к радиусу, соединяющему эту точку с центром сечения, а величина прямо пропорциональна расстоянию точки от центра. В центре (при ρ = 0) касательные напряжения равны нулю; в точках же, расположенных в непосредственной близости от внешней поверхности бруса, они наибольшие. График изменения величин τ вдоль какого-либо радиуса (т.е. эпюра касательных напряжений) изображается прямой линией (рис. 2.2).

Распределение касательных напряжений по сечению при кручении (рис. 2.2)

Касательное напряжение в точке А:

Рис.2.2

(2.3)

где — расстояние от точки А до центра сечения;

М_к – крутящий момент;

J_p - полярный момент инерции в сечении

Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в

;

(круг), (2.4)

(кольцо), (2.5)

где М_к — крутящий момент в сечении, Н·м, Н·мм;

W_p — момент сопротивления при кручении, м³, мм³;

[т_к] — допускаемое напряжение при кручении, Н/м², Н/мм².

Проектировочный расчет, определение размеров по­перечного сечения

сечение – круг: d (2.6)

сечение – кольцо: d (2.7)

где d — наружный диаметр круглого сечения;

d_Bn — внутренний диаметр кольцевого сечения; с = d_BK/d.

Определение рационального расположения колес на валу

Рациональное расположение колес — расположение, при кото­ром максимальное значение крутящего момента на валу — наи­меньшее из возможных. Анализируя эпюру касательных напряжений (рис.2.1) можно отметить, что наибольшие напряжения возникают на поверхности вала, в центральной части они значительно меньше и на продольной оси равны нулю. Следовательно, в сплошном валу материал, находящийся в центральной части в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение.

Условие жесткости при кручении

; G ≈ 0,4E (2.8)

где G — модуль упругости при сдвиге, Н/м², Н/мм²;

Е — модуль упругости при растяжении, Н/м², Н/мм².

[φ_о] — допускаемый угол закручивания, [φ_о] = 0, 54-1 град/м;

J_p — полярный момент инерции в сечении, м⁴, мм⁴.

Проектировочный расчет, определение наружного диаметра сечения

(2.9)

Порядок выполнения работы

1. Построить эпюру крутящих моментов по длине вала для пред­ложенной в

задании схемы.

2. Выбрать рациональное расположение колес на валу и даль­нейшие расчеты

проводить для вала с рационально расположенными шкивами.

3. Определить потребные диаметры вала круглого сечения из расчета на прочность и жесткость и выбрать наибольшее из полу­ченных значений, округлив величину диаметра.

4. Сравнить затраты металла для случая круглого и кольцево­го сечений. Сравнение провести по площадям поперечных сечений валов.

Площадь вала рассчитать в наиболее нагруженном сечении (по максимальному крутящему моменту на эпюре моментов).

Контрольные вопросы

1. Какие деформации возникают при кручении?

2. Какие гипотезы выполняются при деформации кручения?

3. Изменяются ли длина и диаметр вала после скручивания?

4. Какие внутренние силовые факторы возникают при кручении?

5. Что такое рациональное расположение колос на валу?

6. Что такое полярный момент инерции? Какой физический смысл имеет эта величина?

В каких единицах измеряется?

7. Какие внутренние силовые факторы возникают при кручении?

8. Что такое рациональное расположение колес на валу?

9. Как вычисляют значение крутящего момента в поперечном сечении вала?

10. Что такое эпюра крутящего момента и как она строится?

11. Для чего строится эпюра крутящих моментов?

12. В чем заключается расчет на прочность при кручении?

13. В чем заключается расчет на жесткость при кручении?

14. Как определяется диаметр вала из условия прочности?

15. Как определяется диаметр вала из условия жесткости?

Пример выполнения

Для заданного бруса (рис.2.3) построить эпюры крутящих моментов, рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента. Построить эпюру крутящих моментов при рациональном расположении шкивов. Из условия прочности определить диаметры валов для сплошного и кольцевого сечений, приняв с = . Сравнить полученные результаты по полученным площадям поперечных сечений. [τ_k] = 35 МПа.

Дано: ω = 2 рад/с, Р₁ = 0,1 кВт, Р₂ = 0,2 кВт, Р₃ = 0,2 кВт

Решение:

1. Определяем вращающие моменты на шкивах

М₁ = Р₁·ω = 100·2 = 200 Н·м

М₂ = Р₂·ω = 200·2 = 400 Н·м

М₃ = Р₃·ω = 200·2 = 400 Н·м

М₀ = М₁ + М₂ + М₃ = 1000 Н·м

2. Пользуясь методом сечений, определяем крутящие моменты на участках вала (рис.2.3).

Сечение 1 (рис.2.4а):

Сечение 2 (рис.2.4б):

Сечение 3 (рис.2.4в):

Рис.2.3

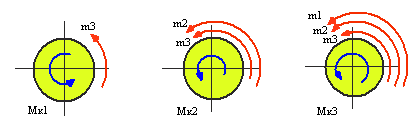
а б в

Рис.2.4

3. Строим эпюру крутящих моментов. Значения крутящих моментов откладываем вниз от оси, т.к. моменты отрицательные. Максимальное значение крутящего момента на валу в этом случае 1000 Н·м (рис.2.3).

4. Выберем рациональное расположение шкивов на валу. Наиболее целесообразно такое размещение шкивов, при котором наибольшие положительные и отрицательные значения крутящих моментов на участках будут по возможности одинаковыми. Из этих соображений ведущий шкив, передающий момент 1000 Н·м, помещают ближе к центру вала, ведомые шкивы 1 и 2 размещают слева от ведущего с моментом 1000 Н·м, шкив 3 остается на том же месте. Строим эпюру крутящих моментов при выбранном расположении шкивов (рис.2.5).

Максимальное значение крутящего момента на валу при выбранном расположении шкивов – 600 Н·м.

Рис.2.5

5. Определяем диаметр вала из условия прочности при условии, что сечение – круг. Условие прочности при кручении:

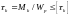
Момент сопротивления кручению:

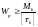
Определяем диаметр вала:

Округляя до ближайшего стандартного значения (СТ СЭВ 514-77), получаем

6. Определяем диаметр вала из условия жесткости

Полярный момент инерции

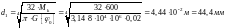
Округляя до ближайшего стандартного значения (СТ СЭВ 514-77), получаем

7. Определяем диаметры вала по сечениям при условии, что сечение - кольцо

Момент сопротивления остается тем же. По условию

Полярный момент сопротивления кольца:

Формула для определения наружного диаметра вала кольцевого сечения:

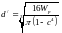
Расчет можно провести по формуле:

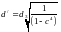
Диаметры вала по сечениям:

Наружные диаметры вала кольцевого сечения практически не изменились.

Для кольцевого сечения:, ,

8. Для вывода об экономии металла, при переходе на кольцевое сечение, сравним площади сечений.

При условии что сечение – круг (рис.2.6а)

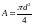
Сплошное круглое сечение:

При условии, что сечение – кольцо, (рис.2.6б) (рис.7.4б)

Кольцевое сечение:

Сравнительная оценка результатов:

Следовательно, при переходе с кругового на кольцевое сечение экономия металла по весу составит 1,3 раза. Выбираем для вала кольцевое сечение.

а б

рис.2.6

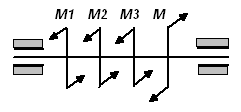
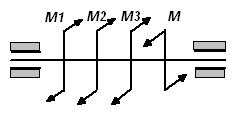
а)	б)
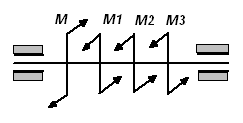
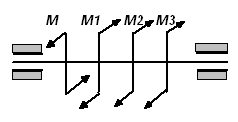
в)	г)

Рис.2.7

Таблица 2.1

№ варианта	№ рис.	ω, рад/с	Р1, кВт	Р2, кВт	Р3 , кВт
1	2.7а	20	40	10	130
2	2.7б	25	20	42	100
3	2.7в	30	18	25	120
4	2.7г	10	30	16	140
5	2.7а	15	56	28	150
6	2.7б	20	35	48	130
7	2.7в	25	17	22	100
8	2.7г	30	40	10	120
9	2.7а	10	20	42	140
10	2.7б	15	18	25	150
11	2.7в	20	30	16	130
12	2.7г	25	56	28	100
13	2.7а	30	35	48	120
14	2.7б	10	17	22	140
15	2.7в	15	40	10	150
16	2.7г	20	20	42	130
17	2.7а	25	18	25	100
18	2.7б	30	30	16	120
19	2.7в	10	56	28	140
20	2.7г	15	35	48	150
21	2.7а	20	17	22	130
22	2.7б	25	40	10	100
23	2.7в	30	20	42	120
24	2.7г	10	18	25	140
25	2.7а	15	30	16	150
26	2.7б	20	56	28	130
27	2.7в	25	35	48	100
28	2.7г	30	17	22	120
29	2.7а	10	40	10	140
30	2.7б	15	20	42	150