7. Анализ факторов интенсификации производства.
7.1. Задание
Имеются данные по группе сельскохозяйственных предприятий об урожайности зерновых культур, возделываемых на орошаемых землях, дозах внесения удобрений и фактической оросительной норме для соответствующего сельскохозяйственного участка.
По имеющимся многочисленным данным для различных сельскохозяйственных предприятий выполнить статистический анализ:
1. Определить основные статистические характеристики статистических совокупностей (средние значения показателя, показатели изменчивости, структурные средние, доверительный интервал для среднего, показатели корреляции урожайности с каждым в отдельности фактором (взаимосвязи урожайности с приведенными факторами).
При выполнении расчетов целесообразно использовать статистические функции Microsoft Excel .
2. Построить уравнение множественной регрессии экономического результата деятельности предприятий и определяющих факторов.
3. Рассчитать прогнозный ряд урожайности для тех же значений факторный переменных и статистический ряд ошибок прогноза; вычислить для полученных рядов статистические характеристики (как и в п.1.), сделать их анализ.
4. Рассчитать коэффициенты корреляции прогнозного ряда и ошибок прогноза с фактической урожайностью.
5. Определить коэффициенты детерминации прогноза и ошибки, сделать вывод о значимости изучаемых факторов интенсификации для роста урожайности, а так же степени влияния прочих неучтенных факторов. Проверить выполнение правила сложения дисперсий для прогноза и его ошибки. Сделать вывод.
6. Сделать оценку качества построенной регрессионной модели для выполнения прогнозных расчетов.
7.2. Теоретические сведения
1. Статистическим совокупностями в нашем примере являются
а) показатели урожайности для различных участков множества предприятий области, сформированными выборочным методом.
б) соответствующий для этих участков величины внесенных удобрений (кг действующего вещества в среднем на один га)
в) соответствующий для тех же участков фактические значения средних оросительных норм при осуществлении поливов, тыс. м3/га.
Для каждого из приведенных рядов установим средние арифметические значения, дисперсию, среднеквадратическое отклонение (стандарт), коэффициент вариации, доверительное отклонение для среднего (предельную ошибку выборки для 95% вероятности), пользуясь известными формулами из курса общей теории статистики, а так же максимум, минимум и медианное значение показателя внутри каждой статистической совокупности.
Обозначим:
Y – урожайность, ц/га;
X1 – доза внесения удобрений (кг действ. вещ.)/га;
X2 – оросительная норма, тыс.м3/ га;
Тесноту взаимосвязи урожайности и факторов интенсификации (внесение удобрений, орошение) определим при помощи линейных коэффициентов корреляции: ry,x1 и ry,x2. Для этого воспользуемся одной из формул:
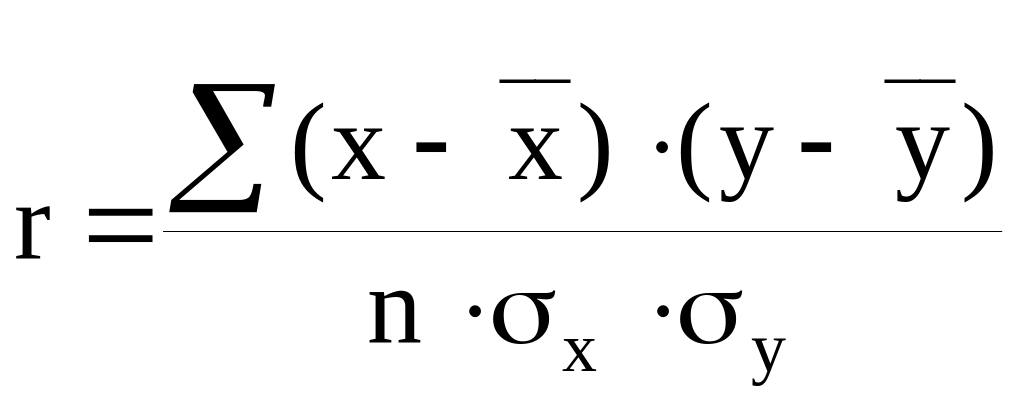
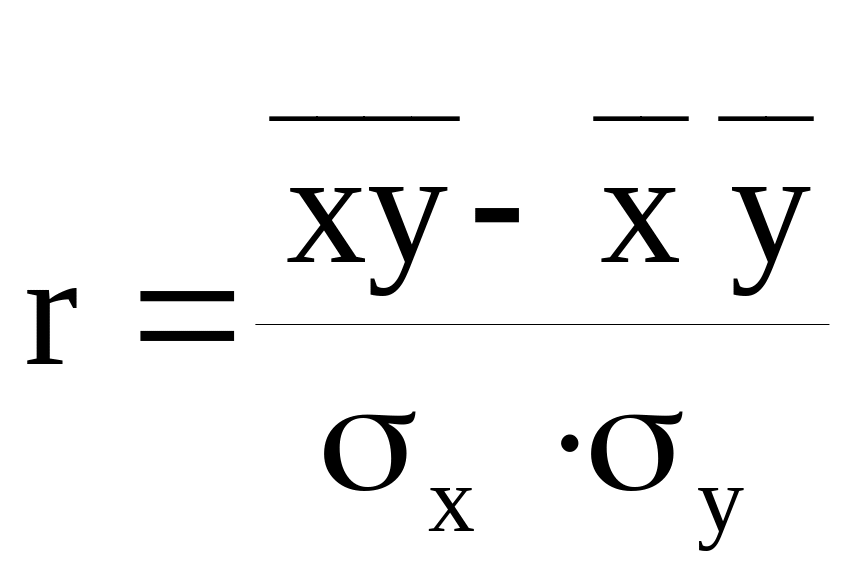
Показателем тесноты связи, устанавливаемой между результативным и двумя факторными признаками является совокупный коэффициент множественной корреляции R.
где r – линейные коэффициенты корреляции (парные), а подстрочные индексы показывают между какими признаками они исчисляются.
Значение R2 называется коэффициентом множественной детерминации. Он показывает совокупную долю совместного вклада рассматриваемых факторов в общую изменчивость изучаемого явления.
2. Теоретической основой изучения взаимной связи урожайности и факторов интенсификации является зависимость следующего вида (теоретическая модель):
Y = a + bX1 + cX2,
где:
a,b,c – коэффициенты уравнения (параметры модели), определяемые методом наименьших квадратов.
Для нахождения коэффициентов a,b,c в соответствии с методом наименьших квадратов следует решить следующую систему уравнений:
Для нахождения решения используется метод главного элемента
3. После нахождения коэффициентов рассчитаем прогнозный ряд YX1,X2 путем подстановки в уравнение регрессии значений X1 и X2
Ряд ошибок прогноза урожайности Δ=(Y-Yx1,x2) вычислим для тех же хозяйств, приняв в качестве исходных данных те же значения факторов интенсификации.
Для построенного ряда значений YX1,X2 и Δ вычислить те же статистические характеристики, что и для исходного ряда урожайности Y, как было сделано выше.
4. Вычислим коэффициенты корреляции прогнозного ряда YX1,X2 и ошибок прогноза Δ с фактической урожайностью Y.
5. Коэффициенты детерминации прогноза и ошибки вычисляются на основе полученных значений дисперсии.
Детерминация прогноза:
детерминация ошибки прогноза:
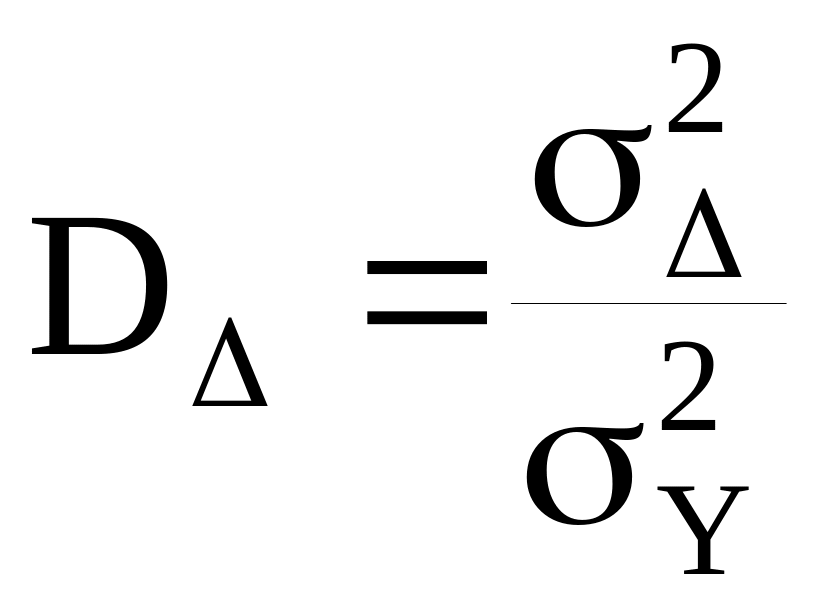
Вывод о значимости факторов определяется по степени близости коэффициента детерминации к 1. Значение коэффициента детерминации, выраженное в процентах показывает долю вклада изучаемых факторов в общую изменчивость явления.
Правило сложения дисперсии (при независимости факторов X1 и X2), устанавливает, что сумма дисперсии прогноза (как результата влияния изучаемых факторов X1 и X2) и дисперсии ошибок (как результата влияния прочих неучтенных в модели факторов) должна быть равна общей дисперсии результативного фактора:
6. Характеристики качества статистической модели прогноза урожайности и ее надежности для выполнения прогнозных расчетов.
Вычисляется показатель:
,
где: Y – фактическая величина урожайности
Yх1,х2 – прогноз,
n – количество членов ряда,
m – число степеней свободы (принимается равным 2),
σ – среднеквадратическое отклонение урожайности.
Критерий качества статистической модели:
- хорошее качество
модели
- удовлетворительное
качество модели
- неудовлетворительное
качество (прогнозная модель практически
не улучшает простейший прогноз «по
среднему»)
Допустимая ошибка прогноза при использовании модели для прогноза рассчитывается по формуле:
