9.6. Многофакторный корреляционно-регрессионный анализ.
Многофакторный корреляционно-регрессионный анализ позволяет оценить меру влияния на исследуемый результативный показатель каждого из включенных в модель факторов. При этом важным условием является отсутствие между факторами функциональной связи.
Математически задача формулируется следующим образом. Требуется найти аналитическое выражение (уравнение множественной регрессии), наилучшим образом отражающее связь факторных признаков с результативным, т.е. найти функцию:
Чаще всего на практике используется линейная форма связи:
Коэффициенты уравнения рассматриваются аналогичным образом, т.е. последовательностью по тесноте, направлению, аналитическому выражению.
Для определения двух факторов множественной регрессии уравнение регрессии принимает следующий вид:
Параметры данного уравнения множественной регрессии определяются путем построения системы нормальных уравнений:
Параметры a1 и a2 уравнения множественной регрессии (показатели интенсивности действия отдельных факторов) показывают среднее приращение результативного признака, обусловленное одиночным приращением i-го фактора не зависимо от изменения остальных учтенных факторов.
Помимо показателя интенсивности для оценки влияния отдельных факторов используется коэффициент эластичности который рассчитывается в относительных величинах (%) по формуле:
Для измерения тесноты связи определяются частные коэффициенты корреляции, которые характеризуют степень влияния одного из аргументов на функцию.
Частный коэффициент первого порядка между признаками y х1 при исключенном влиянии признака х2 вычисляется по формуле:
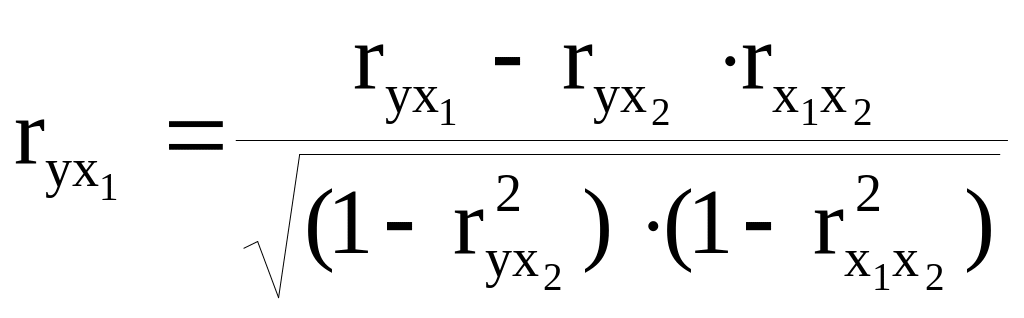
где r – парные коэффициенты корреляции между соответствующими признаками.
Показателем тесноты связи, устанавливаемой между результативным и двумя или более факторными признаками является совокупный коэффициент множественной корреляции R.
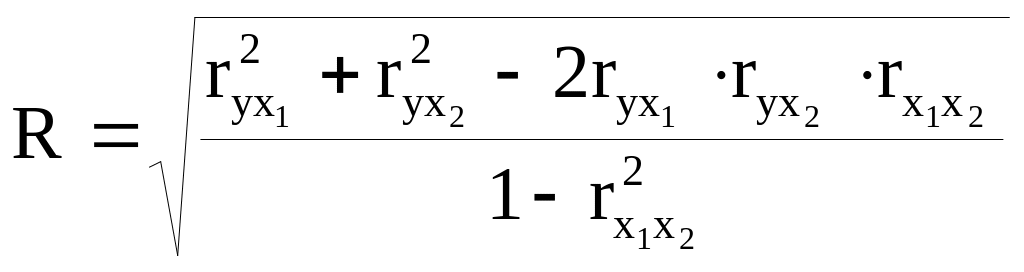
где r – линейные коэффициенты корреляции (парные), а подстрочные индексы показывают между какими признаками они исчисляются.
Значение R2 называется коэффициентом множественной детерминации. Он показывает совокупную долю совместного вклада рассматриваемых факторов в общую изменчивость изучаемого явления.
Уравнение множественной регрессии строится, как правило, для наиболее существенных факторов, влияющих на результативный признак. Чем больше размерность уравнения, тем сложнее вычисления и если для какого-то из факторов связь не очень существенна, то это не оправдано сложностью задачи и точностью получаемого результата. По этому для выбора факторов, включаемых в модель множественной регрессии необходимо провести предварительное исследование связи отдельных факторов с результативным признаком. Это можно получить в частности путем определения парных коэффициентов корреляции и ранжирования факторов по величине коэффициента корреляции. Далее отбираются наиболее значимые из них (с коэффициентом корреляции более 0,7 по абсолютной величине), а остальные отсекаются.