Лекция 17. Корреляционно-регрессионный анализ

9.4. Однофакторный корреляционно-регрессионный анализ

9.5. Показатели тесноты статистической связи.

9.6. Многофакторный корреляционно-регрессионный анализ

9.4. Однофакторный корреляционно-регрессионный анализ

Факторные связи характеризуются тем, что они проявляются в согласованной вариации изучаемых показателей. При этом одни показатели выступают как факторные, а другие — как результативные.

Факторные связи могут рассматриваться как функциональные и корреляционные.

При функциональной связи изменение результативного признака всецело зависит от изменения факторного признака :

При корреляционной связи изменение результативного признака не всецело зависит от факторного признака , а лишь частично, так как возможно влияние прочих факторов :

.

Характерной особенностью корреляционных связей является то, что они проявляются не в единичных случаях, а в массе.

При статистическом изучении корреляционной связи деятельности перед статистикой ставятся следующие основные задачи:

1) проверка положений экономической теории о возможности связи между изучаемыми показателями и придание выявленной связи аналитической формы зависимости;

2) установление количественных оценок тесноты связи, характеризующих силу влияния факторных признаков на результативные.

Для того, чтобы установить, есть ли зависимость между величинами, используются многообразные статистические методы, позволяющие определить, во-первых — какие связи; во-вторых — тесноту связи (в одном случае она сильная, устойчивая, в другом — слабая); в-третьих — форму связи (т.е. формулу, связывающую величину и ).

В процессе изучения связи надо учитывать, что мы используем математический аппарат, но всегда надо иметь теоретические обоснования той связи, которую пытаются показать.

Главным параметрическим методом является корреляционно-регрессионный метод.

В теории корреляции решается две основные задачи: определить теоретическую форму связи (регрессионный анализ) и измерить тесноту существующей связи (корреляционный анализ).

Первая задача состоит в том, чтобы отыскать такую форму функциональной связи, которая в наилучшей степени отвечает сущности обнаруженной корреляционной зависимости.

Вторая задача состоит в том, чтобы измерить с помощью специальных показателей, в какой мере корреляционная связь приближается по своей силе к связи функциональной.

Таким образом, задача заключается в нахождении уравнения связи, в котором результативный признак зависит только от интересующего нас фактора (или нескольких факторов). Все прочие факторы, также влияющие на результат, принимаются за постоянные средние.

При проведении корреляционного анализа необходимо отобрать наиболее существенные признаки, установить связь между ними (причинно-следственную) определить форму связи, выбрать математическое уравнение для отражения данных взаимосвязи.

При установлении характера взаимосвязи между признаками, кроме аналитической группировки большое значение имеет графический метод. Отложив на оси абсцисс значение факторного признака x, а на оси ординат значение результативного признака y, и получив в корреляционном пространстве точки x и y, получим корреляционное поле. Характер расположения этих точек дает представление о направлении и форме связи, а также позволяет построить уравнение парной зависимости.

Наиболее распространенные зависимости, используемые в экономике:

а) Прямая линия:

б) Парабола:

в) Гипербола:

г) Полулогарифмическая кривая:

- результативный признак;

x – факторный признак;

a_0, a_1, a₂… - параметры уравнения (коэффициенты регрессии), которые позволяют рассмотреть среднее значение, т.е. показывают среднее изменение зависимой переменной y от x при изменении независимой переменной x на 1.

Параметры уравнения определяются путем решения системы нормальных уравнений, полученных на основе метода наименьших квадратов:

а) прямая: ;

система уравнений для вычисления параметров a₀, a₁:

;

б) парабола: ;

система уравнений для вычисления параметров a₀, a₁, а₂:

;

в) гипербола:

система уравнений для вычисления параметров a₀, a₁:

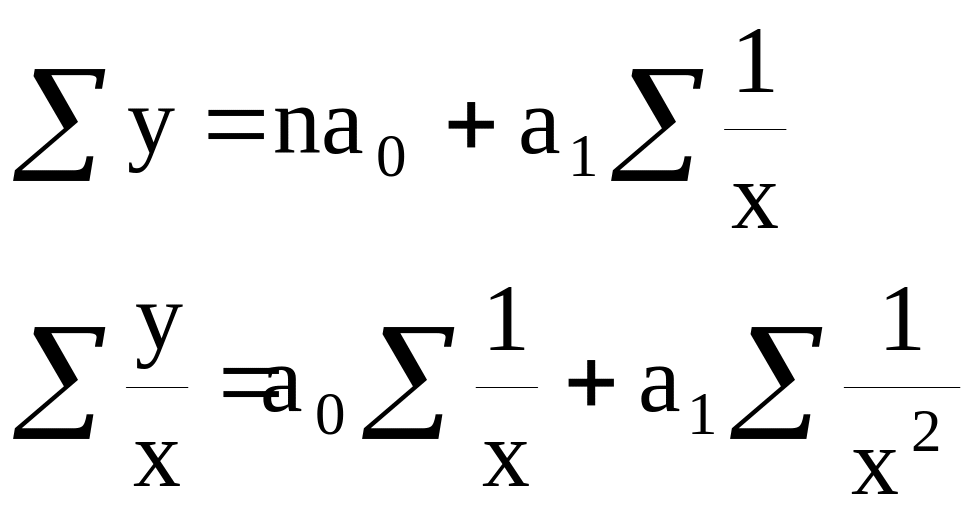
г) полулогарифмическая кривая: ;

система уравнений для вычисления параметров a₀, a₁:

Приведенные выше уравнения связи (уравнения регрессии) выражают функциональную зависимость y от x. Выбор вида зависимости определяется на основе предварительных исследований методами аналитической группировки, а также графическим методом. Можно выполнить расчеты уравнения регрессии различными методами, а затем сравнить различные виды зависимости. Для этого используются специальные методы. Простейший из них – сравнение по коэффициенту корреляции (будет рассмотрен ниже), либо по сумме линейных или квадратичных отклонений расчетных по уравнению значений результативного признака и фактически наблюденных для тех же значений факторного признака.

Уравнение регрессии имеет большую ценность, поскольку позволяют экстраполировать показатели связи за пределы исследованных данных.

Параметры а₁ (а в уравнении параболы и а₂) называются коэффициентами регрессии. В корреляционном анализе эти параметры показывают меру, в которой изменяется у при изменении х на одну единицу.

При линейной зависимости коэффициент регрессии а₁ называется также коэффициентом пропорциональности. Он положителен при прямой зависимости, отрицателен – при обратной. Это параметр показывает в какой мере (в среднем) увеличится y с ростом на единицу величины x, т.е. показывает среднюю величину абсолютного прироста y на единицу факторной переменной x

Параметр же а₀ показывает влияние на результативный фактор множества неучтенных факторов.

Наиболее часто в практике экономических расчетов используется линейная зависимость. В линейном уравнении параметры a₀ и a₁ могут быть вычислены по достаточно простым формулам:

, .

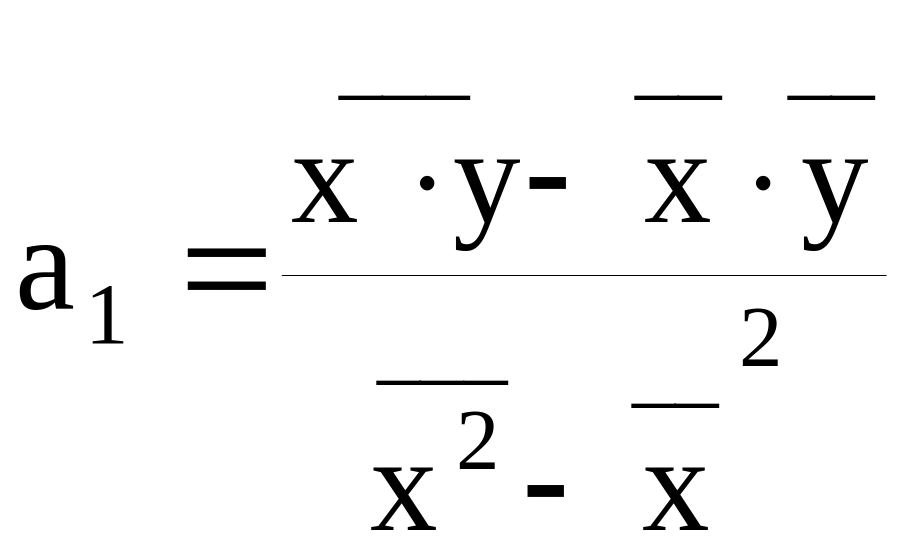Случайная ошибка определения параметров а₁ определяется по формуле:

.

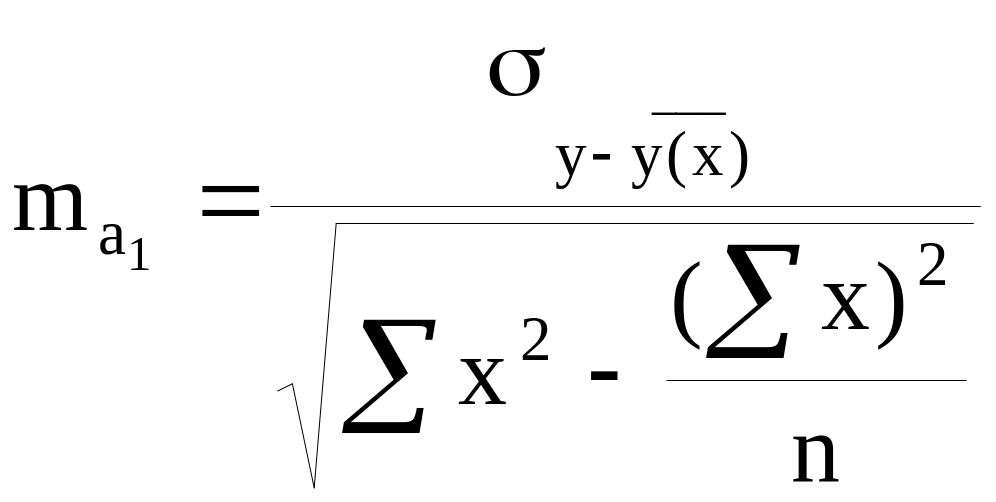Количественную зависимость изменения значения от изменения x, что бывает удобнее выразить в относительных величинах, можно вычислить при помощи коэффициента эластичности.

Коэффициент эластичности показывает, на сколько процентов увеличивается при увеличении x на один процент и рассчитывается по формуле:

.
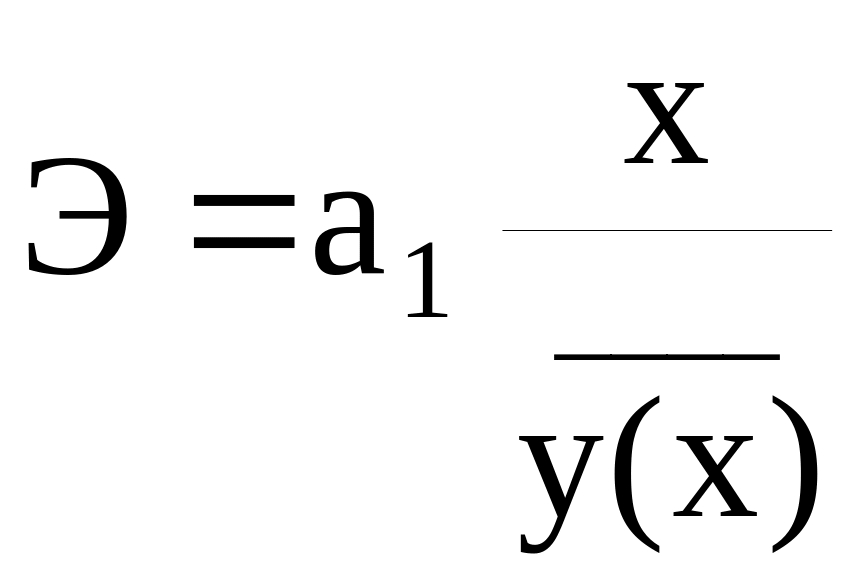