7.3. Понятие предельной ошибки выборки.
Тот факт, что генеральная средняя (или генеральная доля) не выйдет за определенные пределы, можно утверждать не с абсолютной достоверностью, а лишь с определенной степенью вероятности.
Значит, с определенной степенью вероятности, мы можем утверждать, что отклонения выборочных характеристик от генеральных не превысят некоторой величины, которая называется предельной ошибкой выборки.
Предельная ошибка
выборки
связана со средней ошибкой выборки
отношением:
.
При этом t как коэффициент кратности средней ошибки выборки (так называемый, коэффициент доверия) зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.
Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам:
,
.
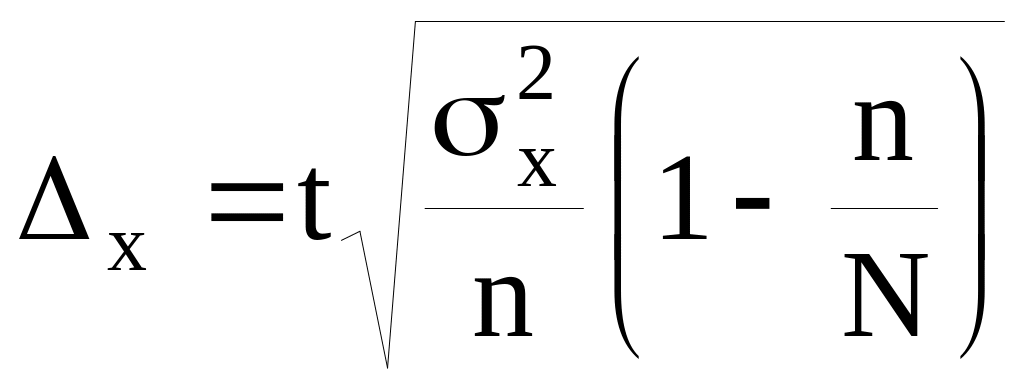Предельная ошибка выборки при повторном отборе определяется по формуле:
,
.
Таблица 45
Значение вероятности при разной величине коэффициента доверия t.
t |
вероятность |
t |
вероятность |
t |
вероятность |
1,0 |
0,6827 |
1,8 |
0,9281 |
2,5 |
0,9876 |
1,1 |
0,7287 |
1,9 |
0,9426 |
2,58 |
0,9900 |
1,2 |
0,7699 |
1,96 |
0,9500 |
2,6 |
0,9907 |
1,3 |
0,8064 |
2,0 |
0,9545 |
2,7 |
0,9931 |
1,4 |
0,8385 |
2,1 |
0,9643 |
2,8 |
0,9949 |
1,5 |
0,8664 |
2,2 |
0,9722 |
2,9 |
0,9963 |
1,6 |
0,8904 |
2,3 |
0,9786 |
3,0 |
0,9973 |
1,7 |
0,9109 |
2,4 |
0,9836 |
3,28 |
0,9990 |
Последнее замечание относится к дисперсии. В математической статистике доказано, что соотношение между генеральной дисперсией и выборочной такое:
Лекция 13. Способы проведения и анализа выборочного наблюдения
7.4. Расчет необходимой численности выборки, доверительных интервалов выборочной оценки, вероятности осуществления заданной ошибки выборки.
7.5. Малая выборка. Способы распространения характеристик выборки на генеральную совокупность.
7.6. Способы отбора единиц из генеральной совокупности.
7.4. Расчет необходимой численности выборки, доверительных интервалов выборочной оценки, вероятности осуществления заданной ошибки выборки.
Приведенные формулы для определения величины ошибки выборки дают возможность не только определять эти ошибки, но и рассчитывать предварительно какую необходимо взять численность выборки, чтобы ошибка выборки не превышала определенных заданных размеров.
1. Для определения необходимой численности выборки следует поступить следующим образом. Если средняя ошибка выборки при выборочном измерении среднего значения показателя определяется по формуле:
,
то
,
отсюда
.
Таким образом, для заданной ошибки выборки , численность выборки при изменении средней будет равна среднему квадрату отклонений, деленному на квадрат заданной точности.
Если оперировать понятиями предельной ошибки выборки, то будем иметь:
.
Аналогичным образом из формулы ошибки выборки для бесповторного отбора находят, что числитель выборки для среднего значения показателя будет рассчитываться по следующей формуле.
При выборочном измерении доли признака необходимая численность выборки определяется по формуле:
Если же использовать предельную ошибку выборки, то получим:
.
Таким образом, чтобы определить необходимую численность выборки необходимо задать 1) требуемый уровень надежности, определяемый коэффициентом доверия t, зависящего от вероятности осуществления заданной ошибки выборки и 2) самой (приемлемой для нас) величины ошибки выборки . Для нахождения t, соответствующего назначенной вероятности, следует обратиться к приведенной выше таблице.
2. Для определения доверительных интервалов для среднего и доли, т.е. таких интервалов в пределах которых может находиться искомая величина в генеральной совокупности следует:
1) задать требуемый уровень надежности (вероятности осуществления заданной ошибки выборки) и соответствующий этой вероятности коэффициент доверия t.
2) задать или определить величину дисперсии в генеральной совокупности
3) задать численность выборки n.
А затем следует воспользоваться формулами (для схемы повторного отбора):
для средней:
для доли:
.
3. Для определения какова будет вероятность осуществления заданной ошибки выборки следует:
1) задать величину предельной ошибки выборки .
2) задать или определить величину дисперсии в генеральной совокупности
3) задать численность выборки n.
А затем следует воспользоваться формулами для определении t (для схемы повторного отбора):
для средней:
для доли:
Далее для полученного t по таблице соответствия коэффициентов доверия и вероятности, получим искомое значение вероятности осуществления заданной ошибки выборки.