6.4. Определение среднего абсолютного прироста, средних темпов роста и прироста.
По показателям изменения уровней ряда динамики (абсолютные приросты, темпы роста и прироста), полученным в результате анализа исходного ряда, могут быть рассчитаны обобщающие показатели в виде средних величин - средний абсолютный прирост, средний темп роста, средний темп прироста.
Средний абсолютный прирост может быть получен по одной из формул:
или
,
где n - число уровней ряда динамики;
- первый уровень
ряда динамики;
-
последний уровень ряда динамики;
- цепные абсолютные приросты.
Средний темп роста можно определить, пользуясь формулами:
где n - число рассчитанных цепных или базисных темпов роста;
- уровень ряда,
принятый за базу для сравнения;
- последний уровень ряда;
- цепные темпы
роста (в коэффициентах);
-
последний базисный темп роста.
Между темпами
прироста
и темпами роста К существует соотношение
=
К - 1, аналогичное соотношение верно и
для средних величин.
Лекция 11. Анализ тенденций в рядах динамики
6.5. Определение в рядах динамики общей тенденции развития. Методы укрупненных и скользящих средних.
6.6. Метод аналитического выравнивания рядов динамики.
6.7. Определение в рядах внутригодовой динамики.
6.5. Определение в рядах динамики общей тенденции развития. Методы укрупненных и скользящих средних.
Одним из методов анализа и обобщения динамических рядов является выявление его основной тенденции - тренда.
Определение уровней ряда динамики на протяжении длительного периода времени обусловлено действием ряда факторов, которые неоднородны по силе и направлению воздействия, оказываемого на изучаемое явление.
Рассматривая динамические ряды, пытаются разделить эти факторы на постоянно действующие и оказывающие определяющее воздействие на уровни ряда, формирующие основную тенденцию развития, и случайные факторы, приводящие к кратковременным изменениям уровней ряда динамики.
Наиболее важна при анализе ряда динамики его основная тенденция развития, но часто по одному лишь внешнему виду ряда динамики ее установить невозможно, поэтому используют специальные методы обработки, позволяющие показать основную тенденцию ряда. Методы обработки используются как простые, так и достаточно сложные.
В статистической практике выявление основной тенденции развития осуществляют двумя способами: сглаживания и аналитического выравнивания.
Сглаживание - это механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней (используется метод укрупнения интервалов или скользящее сглаживание);
выравнивание аналитическое - это выравнивание с применением кривой, проведенной между конкретными фактическими уровнями таким образом, чтобы она отражала тенденцию, присущую ряду, освобождая его от незначительных колебаний.
Простейший способ обработки ряда динамики, применяемый с целью установления закономерностей развития - метод укрупнения интервалов.
Суть метода в том, чтобы от интервалов, или периодов времени, для которых определены исходные уровни ряда динамики, перейти к более продолжительным периодам времени и посмотреть, как уровни ряда изменяются в этом случае, поскольку в результате осреднения случайные колебания нивелируются и остается главная составляющая, выражающая тенденцию развития или по другому - тренд.
Пример.
Данные о реализации молочной продукции в магазинах города по месяцам представлены таблицей (в тоннах)
Таблица 42
месяц |
2001 г. |
2002 г. |
2003 г. |
январь |
5,3 |
5,3 |
5,4 |
февраль |
5,3 |
5,1 |
5,2 |
март |
7,9 |
8,3 |
8,2 |
апрель |
8,2 |
9,0 |
9,3 |
май |
9,8 |
9,5 |
10,1 |
июнь |
12,5 |
13,0 |
13,1 |
июль |
11,8 |
12,2 |
12,5 |
август |
10,3 |
10,4 |
10,8 |
сентябрь |
8,2 |
8,0 |
8,3 |
октябрь |
6,5 |
6,6 |
6,8 |
ноябрь |
5,4 |
5,5 |
5,7 |
декабрь |
5,5 |
5,5 |
5,6 |
итого за год |
96,7 |
98,4 |
101 |
Исходные уровни ряда динамики подвержены сезонным изменениям; для определения общей тенденции развития переходят от ежемесячных уровней к годовым уровням:
1987г. - 96,7 тонн
1988г. - 98,4 тонн
1989г. - 101 тонна
Эти цифры, полученные в результате перехода к годовым уровням ряда динамики, показывают общую тенденцию роста реализации молочной продукции.
Или другой пример - ряд суточного выпуска продукции заменить рядом ежемесячного выпуска продукции. Таким образом, сглаживаются суточные колебания выпуска.
Другой способ
определения тенденции в ряду динамики
— метод
скользящих средних.
Сглаживание методом простой скользящей
средней, заключается в том, что вычисляется
средний уровень из трех, пяти, семи и
т.д. уровней. Таким образом, вместо
каждого уровня ряда берутся средние из
окружающих его уровней с обеих сторон.
В этой средней сглаживаются случайные
отклонения. Она будет скользящей,
поскольку период осреднения все время
меняется. Из него вычитается один
предыдущий и прибавляется один следующий.
Например, скользящая средняя из 3-х
уровней будет
,
и т.д. Средняя скользящая относится в
этом случае ко 2-му, 3-му, 4-му и т.д. периоду.
Если скользящая средняя находится по
четному число членов, то для отнесения
ее к конкретному периоду необходимо
произвести центрирование,
т.е. найти среднюю из двух смежных
скользящих средних. Недостаток метода
простой скользящей средней в том, что
сглаженный ряд динамики сокращается
(укорачивается) для начала и конца.
Таким образом, фактические уровни ряда заменяются средними уровнями, вычисленными по определённому правилу. Возьмем другой пример – скользящее сглаживание на интервале не 3, как в предыдущем примере а 5.
Пусть
— исходные или фактические уровни ряда
динамики. Заменим их средними уровнями:
...
...
...
В результате
получается сглаженный ряд, состоящий
из скользящих пятизвенных средних
уровней
.
Между расположением уровней
и
устанавливается соответствие:
— —
— — ,
сглаженный ряд
короче исходного на число уровней
,
где k - число уровней, выбранных для
определения средних уровней ряда или
период сглаживания. Таким образом
информация о крайних членах рядя
теряется.
Сглаживание методом скользящих средних можно производить по четырём, пяти или другому числу уровней ряда, используя соответствующие формулы для усреднения исходных уровней. Чем больше период сглаживания, тем отчетливее просматривается тенденция, однако и больше потерь информации о крайних членах. Поэтому приходится чаще всего ограничиваться тремя – пятью периодами сглаживания, не больше.
Полученные путем сглаживания средние уровни называются трехзвенными, четырёхзвенными, пятизвенными скользящими средними и т.д.
При сглаживании
ряда динамики по чётному числу уровней
выполняется, как уже было сказано,
дополнительная операция, называемая
центрированием, поскольку, при вычислении
скользящего среднего, например по
четырём уровням,
относится к временной точке между
моментами времени, когда были зафиксированы
фактические уровни
и
.
Схема вычислений и расположений уровней
сглаженного ряда становится сложнее:
... — исходные
уровни;
— —
...
— сглаженные уровни;
— —
...
— центрированные сглаженные уровни;
.
Метод скользящих средних не позволяет получить численные оценки для выражения основной тенденции в ряду динамики, давая лишь наглядное графическое представление.
Пример.
Таблица 43.
Годы |
Сбор зерновых в регионе, млн. т. |
Скользящая средняя по 5 уровням |
1980 |
4,3 |
— |
1981 |
4,5 |
— |
1982 |
4,3 |
4,72 |
1983 |
5,2 |
5,00 |
1984 |
5,3 |
5,30 |
1985 |
5,7 |
5,64 |
1986 |
6,0 |
5,78 |
1987 |
6,0 |
5,86 |
1988 |
5,9 |
6,10 |
1989 |
5,7 |
6,32 |
1990 |
6,9 |
6,58 |
1991 |
7,1 |
6,94 |
1992 |
7,3 |
7,48 |
1993 |
7,7 |
7,68 |
1994 |
8,4 |
7,92 |
1995 |
7,9 |
8,22 |
1996 |
8,3 |
8,38 |
1997 |
8,8 |
8,54 |
1998 |
8,5 |
8,94 |
1999 |
9,2 |
9,18 |
2000 |
9,9 |
9,30 |
2001 |
9,6 |
— |
2002 |
9,3 |
— |
На рис. 17 показан график, построенный по данным о валовом сборе зерна в регионе за ряд лет наблюдения и по расчетным данным, представленным в таблице 43.
годы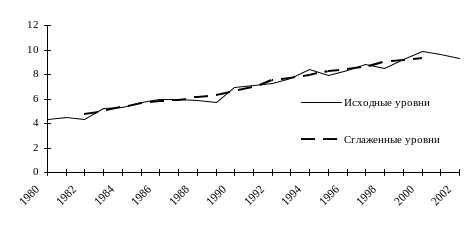
Рис. 17. Валовой сбор зерна в регионе