Лекция 9. Изучение важнейших свойств статистической вариации

5.4. Свойства дисперсии. Расчет дисперсии по формуле по индивидуальным данным и в рядах распределения.

5.5. Показатели относительного рассеивания.

5.6. Общая, межгрупповая и внутригрупповая дисперсии. Правило сложения дисперсий.

5.4. Свойства дисперсии. Расчет дисперсии по формуле по индивидуальным данным и в рядах распределения.

Техника вычисления дисперсии сложна, а при больших значениях вариант и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.

Свойства дисперсии.

1. Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.

1. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.

1. Уменьшение или увеличение каждого значения признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в 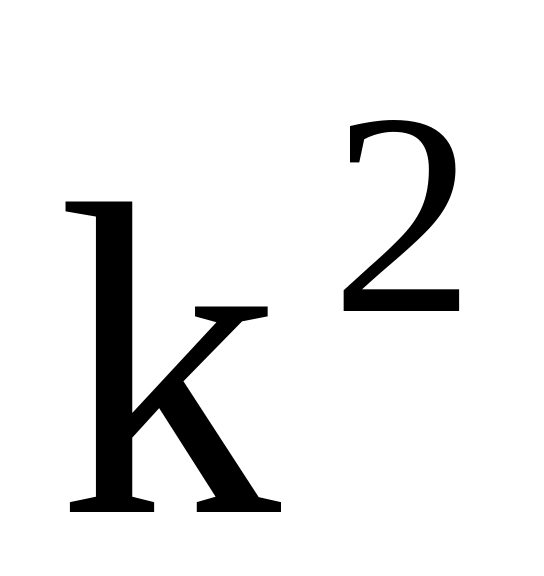раз, а среднее квадратическое отклонение - в к раз.

1. Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной: 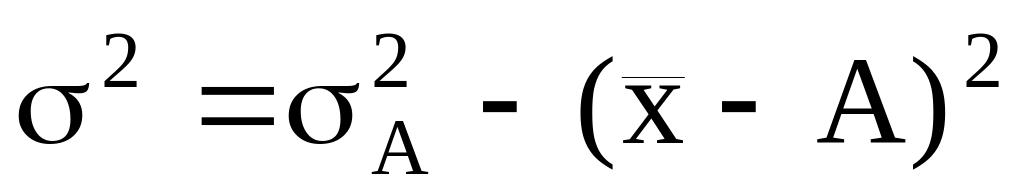. Если А равно нулю, то приходим к следующему равенству: 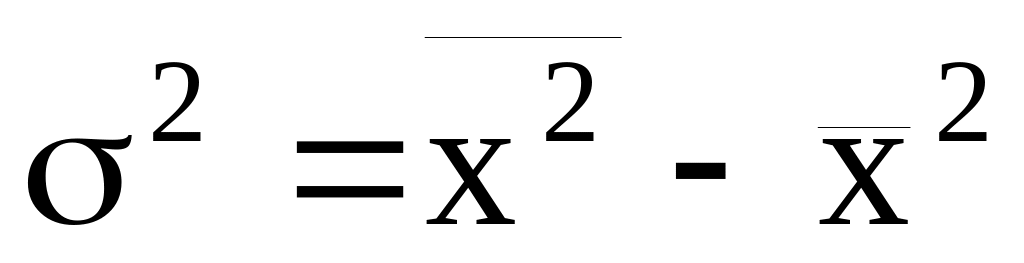, т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.

Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.

Порядок расчета дисперсии простой:

1) определяем среднюю арифметическую ;

2) возводим в квадрат среднюю арифметическую ;

3) возводим в квадрат каждую варианту ряда ;

4) находим сумму квадратов вариант ;

5) делим сумму квадратов вариант на их число, т.е. определяют средний квадрат ;

6) определяют разность между средним квадратом признака и квадратом средней .

Приведем пример использования данной формулы для расчета дисперсии

Имеются следующие данные о производительности труда рабочих:

Таблица 36

Табельный номер рабочего	Произведено продукции, шт.
1	8	64
2	9	81
3	10	100
4	11	121
5	12	144
ИТОГО	50	510

Произведем следующие расчеты:

шт.

Теперь приведем пример расчета дисперсии в дискретном ряду распределения используя данные нижеследующей таблицы.

Таблица 37.

Произведено продукции 1 рабочим, шт. (х)	Число рабочих, n
8	7	56	64	448
9	10	90	81	810
10	15	150	100	1500
11	12	132	121	1452
12	6	72	144	864
ИТОГО	50	500	510	5074

Рассмотрим расчет дисперсии в интервальном ряду распределения.

Порядок расчета дисперсии взвешенной по формуле будет следующий:

1. определяем среднюю арифметическую ;

2. возводим в квадрат полученную среднюю ;

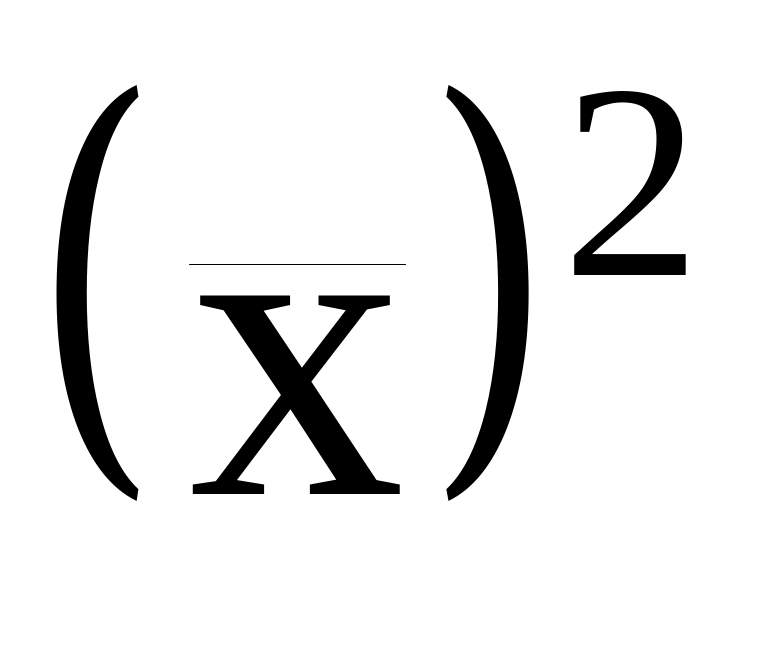3. возводим в квадрат каждую варианту ряда ;

4. умножаем квадраты вариант на частоты ;

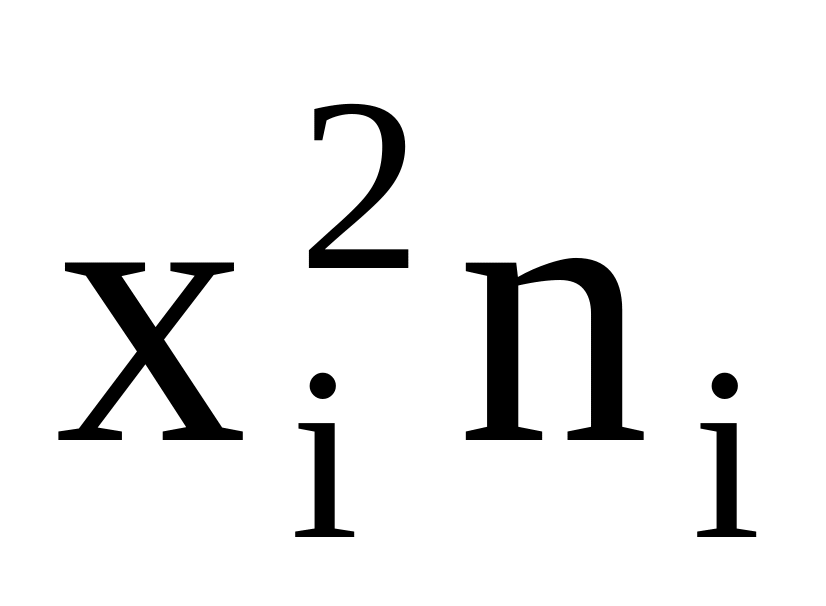5. суммируем полученные произведения ;

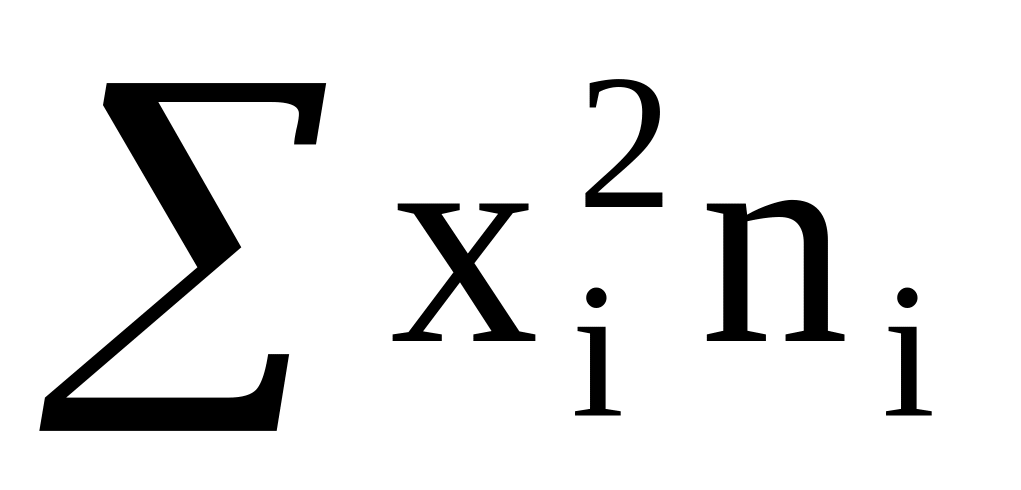6. делим полученную сумму на сумму весов и получаем средний квадрат признака ;

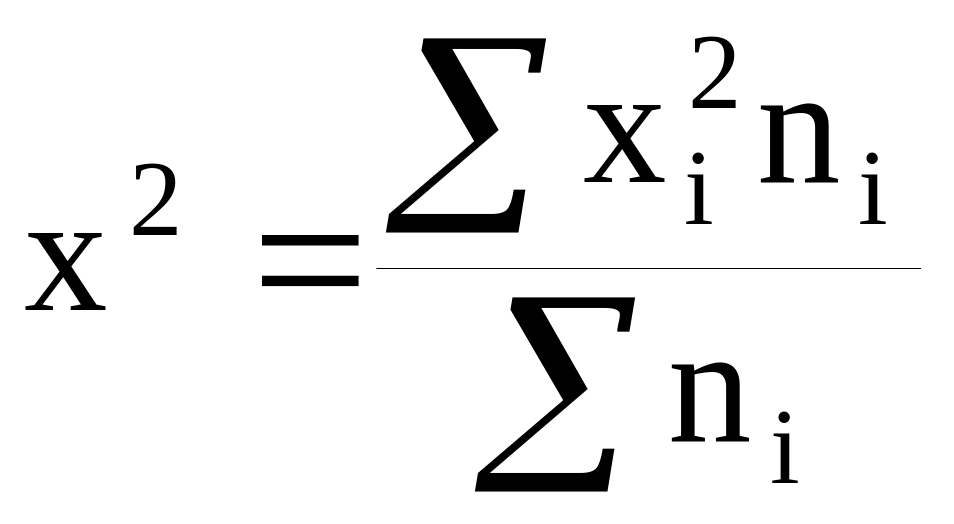7. определяем разность между средним значением квадратов и квадратом средней арифметической, т.е. дисперсию .

Приведем пример.

Имеются следующие данные о распределении посевной площади сельскохозяйственного предприятия по урожайности пшеницы:

Таблица 38

Урожайность пшеницы, ц/га	Посевная площадь, га
14 - 16	100	15	1500	225	22500
16 - 18	300	17	5100	289	36700
18 - 20	400	19	7600	361	144400
20 - 22	200	21	4200	441	88200
ИТОГО	1000		18400		341200

В подобных примерах прежде всего определяется дискретное значение признака в каждом интервале, а затем применяется метод расчета, указанный выше:

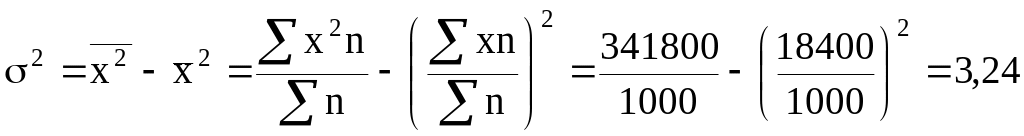
Делая вывод о значении средних величин и показателей вариации можно сказать, что средняя величина отражает тенденцию развития, т.е. действие главных причин (общий уровень развития явления), а среднее квадратическое отклонение измеряет силу воздействия прочих факторов.