3.5. Классификация статистических графиков

При всем своем многообразии статистические графики в курсе “Общая теория статистики” классифицируются по ряду признаков: способу построения, форме применяемых графических образов, характеру решаемых задач.

По способу построения статистические графики подразделяются на диаграммы, картограммы и картодиаграммы.

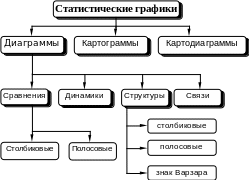
Рис. 3. Виды статистических графиков

Диаграмма представляет чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков.

Диаграмма сравнения — показывает соотношение признака статистической совокупности.

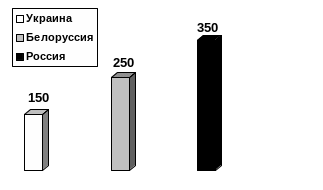
Рис. 4. Столбиковая диаграмма сравнения.

Каждое значение изучаемого показателя изображается в виде вертикального столбика. Количество столбиков определяется числом изучаемых показаний (данных). Расстояние между столбиками должно быть одинаковым. У основания столбиков делается название изучаемого показателя.

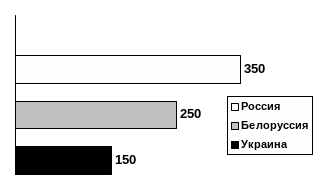
Рис. 5. Полосовая диаграмма сравнения.

В этих диаграммах основания столбиков располагаются вертикально. Должна быть одинаковая ширина полос.

Эту же диаграмму можем построить иначе (рис. 6).

При построении столбиковых диаграмм используется, как и в линейных графиках, прямоугольная система координат.

По оси абсцисс размещается основание столбиков. Их ширина может быть произвольной, но обязательно одинаковой для каждого столбика.

Рис. 6. Столбиковая диаграмма сравнения.

Основные требования построения данных диаграмм:

• соответствие столбиков по высоте, а полос - по длине, отображаемым цифрам;

• недопустимость разрывов масштабной шкалы и начала ее не от нулевой отметки.

Структурная диаграмма - позволяет сопоставить статистические совокупности по составу.

Рис. 7. Структурно-столбиковая диаграмма.

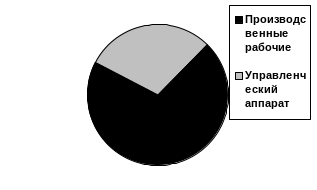
Рис. 8. Структурно-секторная диаграмма

Секторная диаграмма строится таким образом, чтобы каждый сектор занимал площадь круга пропорционально удельному весу отображаемых частей целого. Затем необходимо найти значения центральных углов (1%=3,6 градуса).

Пример.

Таблица 18

Вид культуры	Посевная площадь, га
Зерновые	570,6
Технические	105,6
Картофель	27,9
Кормовые	299,0
ИТОГО	1003,1

Определяем относительные величины структуры использования посевных площадей колхозами.

Зерновые - 570,6/1003,1*100%=56,9%

Картофель - 27,9/1003,1*100%=2,8% и т.д.

Получаем следующие данные (табл. 19).

Таблица 19

Вид культуры	Посевная площадь в колхозах, %
Зерновые	56,9
Технические	10,5
Картофель	2,8
Кормовые	29,8
ИТОГО	100,0

Определяем по данным об удельных весах посевных площадей, занятых под отдельными культурами, соответствующие значения центральных углов.

Зерновые 56,9*360 ⁰/100 = 204,85 ⁰

Технические 10,5*360 ⁰/100 = 37,85 ⁰

Картофель 2,8*360 ⁰/100 = 10,15 ⁰

Кормовые 29,8*360 ⁰/100 = 107,35 ⁰

Теперь строим секторную диаграмму, разделив круг на сектора, в соответствии с полученными значениями центральных углов, культуры:

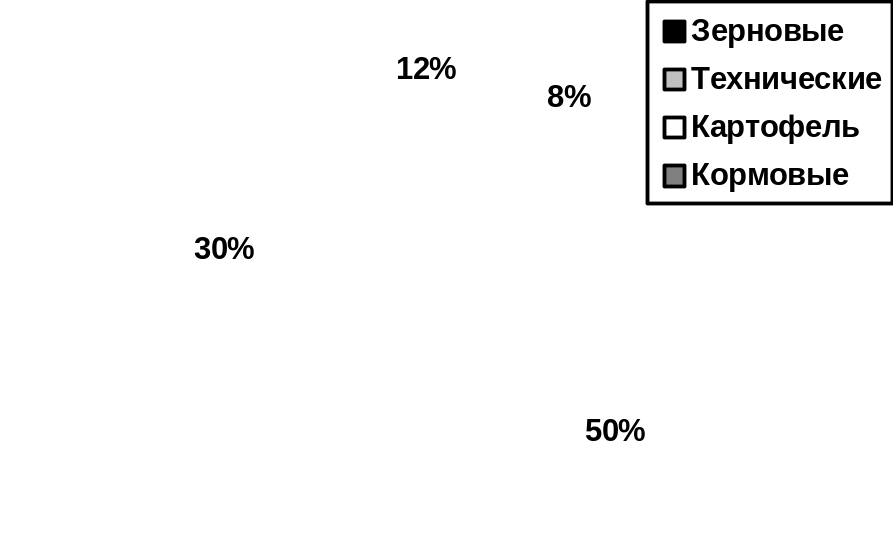
Рис. 9. Структура посевных площадей в хозяйствах области за 2004 г..

При изучении статистической информации о коммерческой деятельности на рынке товаров и услуг применяются так называемые радиальные диаграммы. Строятся они на базе полярных координат. Началом отсчета в них служит центр окружности, а носителем масштабных шкал являются радиусы круга. Обычно в основе радиальных диаграмм лежат повторяющиеся годовые циклы с помесячными или поквартальными данными. Так, при изучении годового цикла с помесячными данными окружность делят радиусами на 12 равных частей. Каждому радиусу дается название месяца года, а их расположение подобно циферблату часов. На каждом радиусе, в соответствии с установленным масштабом, наносятся точки, соответствующие изучаемым за каждый месяц данным. Полученные таким образом точки соединяются между собой линиями

В результате получается спиралеобразная линия, характеризующая внутригодовые циклы коммерческой деятельности.

Знак Варзара. - (Варзар В.Е. - 1851-1940).

Известный русский статистик В. Е. Варзар предложил использовать прямоугольные фигуры для графического изображения трех показателей, один из которых является произведением двух других. В каждом таком прямоугольнике основание пропорционально одному из показателей — сомножителей, а высота его соответствует второму показателю — сомножителю. Площадь прямоугольника равна величине третьего показателя, являющегося произведением двух первых. Располагая рядом несколько прямоугольников, относящихся к разным показателям, можно сравнивать не только размеры показателя — произведения, но и значения показателей — сомножителей.

Приведем пример.

Валовой сбор с/х культуры равен произведению урожайности и посевной площади (рис. 10).

На этом графике можно сравнить между собой:

• урожайность (по длине основания);

• посевные площади (по длине боковой стороны);

• валовой сбор (по площади прямоугольника).

105,7

П

5,9

осевная

площадь

а) б)

Урожайность Урожайность

Рис 10. Валовой сбор, урожайность и посевные площади в 2004 г.

а - зерновых культур,

б - подсолнечника.

Диаграмма динамики - показывает изменение явления во времени. Диаграмма изменений может быть изображена с помощью уже рассмотренных типов диаграмм.

Диаграмма связи - показывает функциональную зависимость одного признака от другого (обычный график на координатной сетке - y = f(x)).

Рис 11. Диаграмма связи.

Статистическая карта - вид графика, который иллюстрирует содержание статистических таблиц, где подлежащим является административное или географическое деление совокупности. На лист изображения наносится контурная географическая карта, отражающая деление совокупности на группы. Статистическая карта называется картограммой, вся информация на ней отображается в виде штриховки, линий, точек, окраски, отражающих изменение какого-либо показателя.

На картодиаграмме, на фоне карты, присутствуют элементы диаграммных фигур. Преимущество картодиаграммы перед диаграммой состоит в том, что она не только дает представление о величине изучаемого показателя на различных территориях, но и изображает пространственное размещение изучаемого показателя.

В зависимости от формы применяемых графических образов статистические графики могут быть точечными, линейными, плоскостными и фигурными.

В точечных графиках в качестве графических образов применяется совокупность точек.

В линейных графиках графическими образами являются линии.

Для плоскостных графиков графическими образами являются геометрические фигуры: прямоугольники, квадраты, окружности.

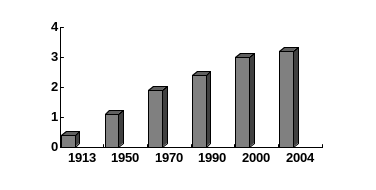
Рис. 12. Потребление кожаной обуви на душу населения

в России в 1913 — 2004 гг. (пар в год).

Данная форма графического изображения уровней ряда динамики удобна тем, что расстояние столбиков друг от друга не зависит от величины интервалов времени.

Представим графически полученные в расчетах базисные относительные величины динамики. Для этой цели чаще всего используется линейная диаграмма (рис. 13.). В системе координат нанесем на ось ординат базисные темпы роста (в процентах), а на ось абсцисс — показания времени.

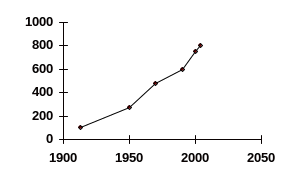
Рис. 13. Темпы роста потребления кожаной обуви в