Линия тренда
На практике часто приходится иметь дело не с функциональными зависимостями, а с табличными данными. Это могут быть данные, полученные в ходе физического эксперимента, социологического опроса, анализа деятельности фирмы и др. Эти результаты, как правило, содержат в себе погрешности. К примеру, при физическом эксперименте это погрешности измерительной аппаратуры. Результаты социологического опроса зависят от настроения интервьюируемого и от формулировки вопроса. В любом случае отклонения от ожидаемого значения могут быть как со знаком плюс, так и со знаком минус. Сгладить эти погрешности поможет линия тренда. Ее график проходит таким образом, чтобы сумма квадратов отклонений табличных значений от линии тренда была минимальной. Выделив график, щелчком ПКМ получается контекстное меню в котором выбирается команда Добавить линию тренда (рис. 2.3.5).
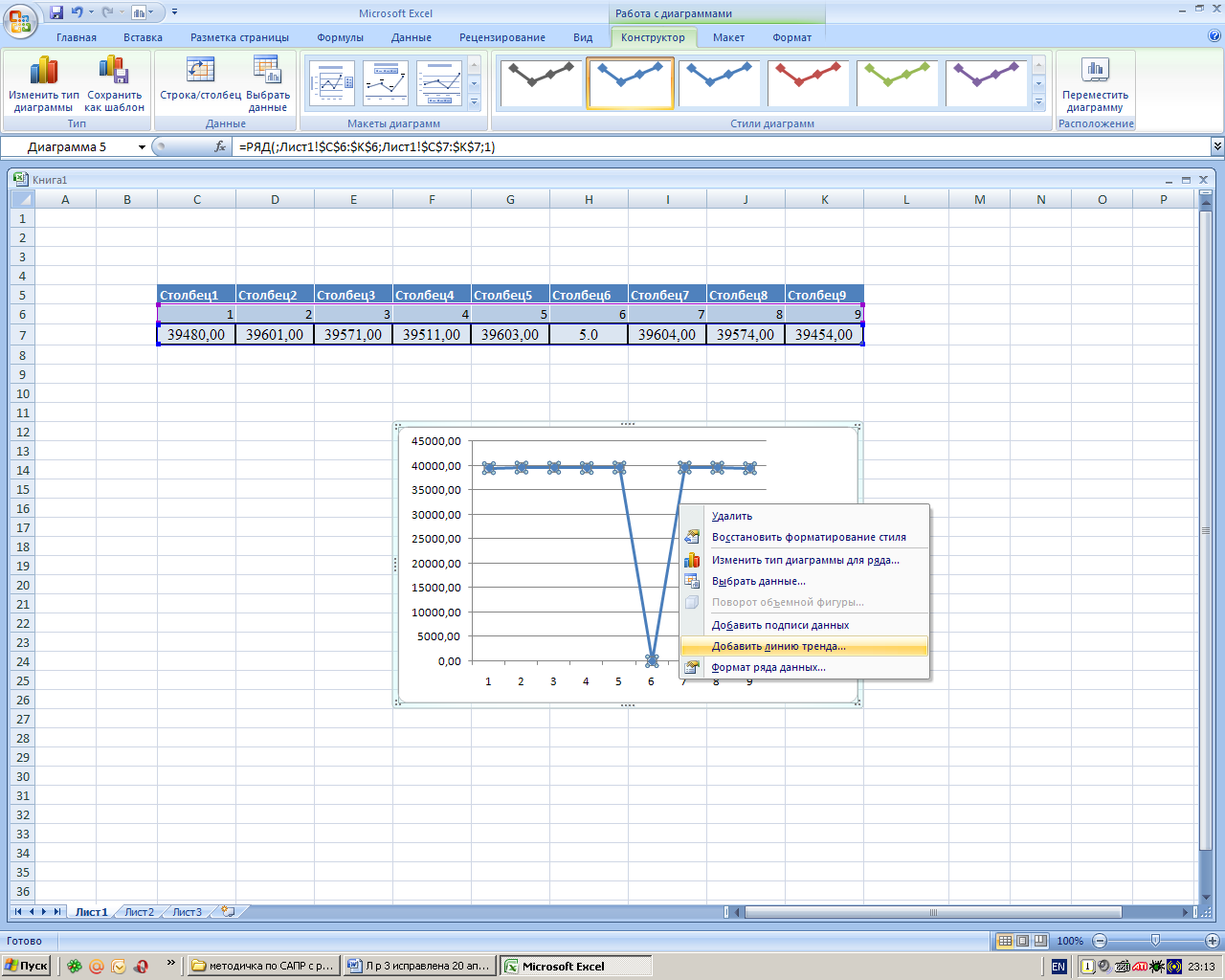
Рис. 2.3.5. Работа с линией тренда
В диалоговом окне выбирается тот тип линии, который наилучшим образом подходит для описания табличных данных(рис. 2.3.6).
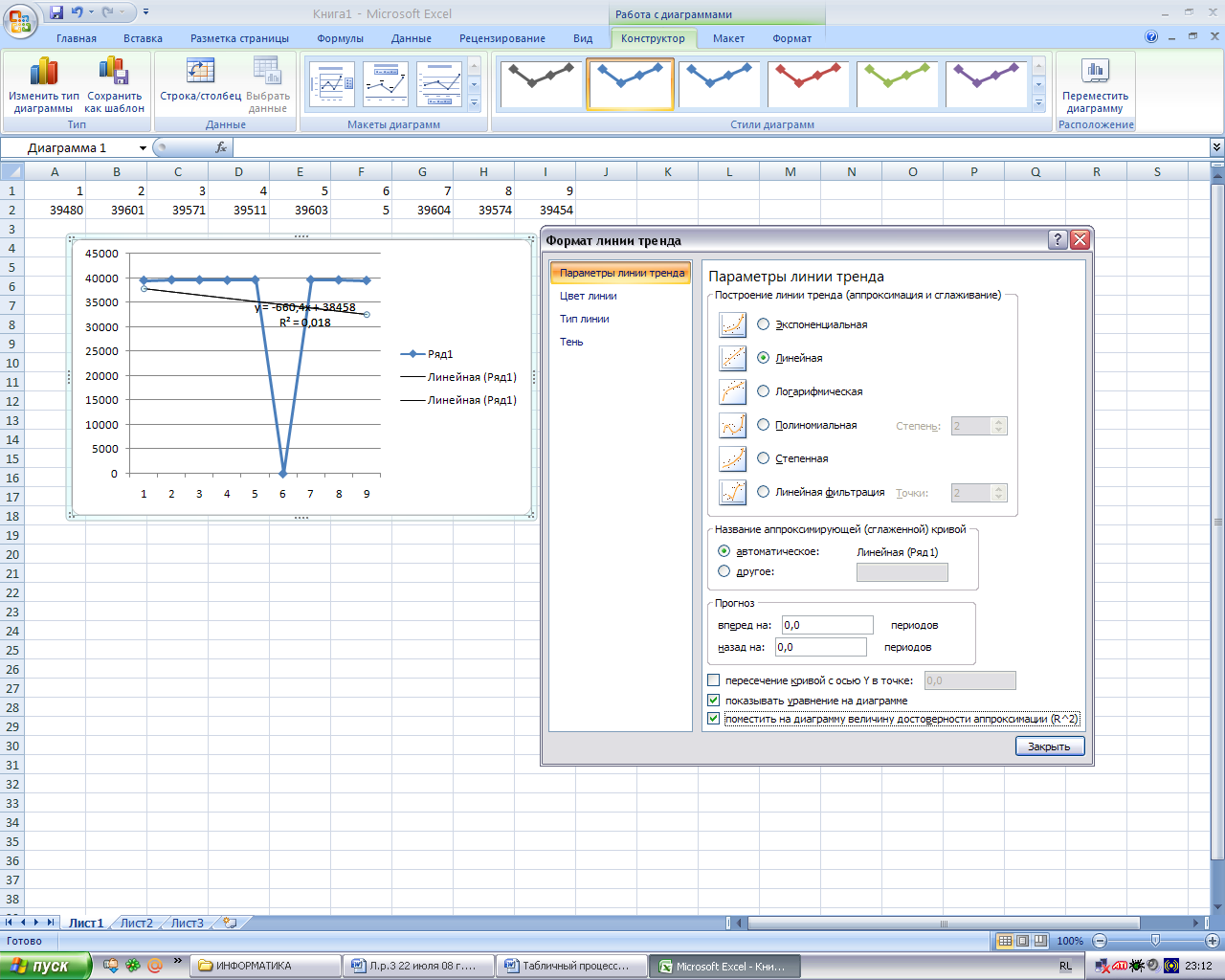
Рис. 2.3.6. Работа с линией тренда
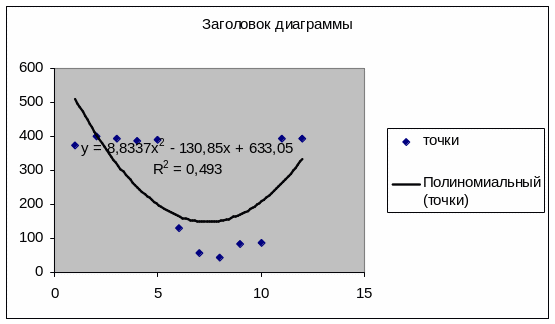
Рис. 2.3.7. Линия тренда
Полученная аналитическая зависимость называется уравнением регрессии (рис. 2.22). Оно удобно не только тем, что позволяет сглаживать погрешности, накопленные в исходных данных, но и рассчитывать значения, не содержащиеся в таблице (проводить интерполяцию и экстраполяцию).
Очень
важной характеристикой регрессионных
зависимостей является мера их
достоверности, которая оценивается
величиной R2,
находящейся в пределах
При
R2=0
величины, для которых определяются
уравнения регрессии, являются независимыми.
При R2=1
имеет место функциональная (а не
статистическая зависимость). Принято
считать допустимым
При
этих значениях данную зависимость можно
использовать для предсказания результата.
Варианты заданий
Варианты заданий для работы приведены в таблицах 2.3.2 – 2.3.5.
Задание 1
Построить на одной координатной сетке графики трех функций согласно полученному варианту. В легенде добавить соответствующие подписи. Дважды щелкнув ЛКМ на рисунке и по линии графика, поэкспериментировать с цветом и типом линий графика.
Y1=аx-в;
Y2=х2+вx+с;
Y3=x3-вx .
Таблица 2.3.2
Исходные данные
№ вар. |
коэффициент - а |
коэффициент - в |
коэффициент - с |
х - принадлежит промежутку |
Шаг изменения х |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
1 |
2.2 |
3.1 |
[-2,2] |
0.1 |
2 |
1.2 |
2.5 |
3.2 |
[-5,5] |
0.23 |
3 |
1.4 |
2.7 |
3.3 |
[-8,5] |
1.3 |
4 |
1.6 |
2.8 |
3.4 |
[-8,8] |
1.2 |
5 |
1.8 |
3.2 |
0.3 |
[-4,5] |
1 |
6 |
2 |
3.5 |
4.2 |
[-4,4] |
1.1 |
7 |
2.2 |
3.8 |
0.22 |
[-7,5] |
0.9 |
8 |
2.5 |
4 |
3.7 |
[-7,7] |
0.87 |
9 |
2.7 |
1.5 |
0.5 |
[-9,5] |
0.99 |
10 |
2.8 |
1.7 |
0.7 |
[-6,5] |
0.2 |
11 |
3.2 |
2.1 |
0.9 |
[-5,6] |
0.22 |
12 |
3.5 |
2.3 |
1 |
[-4,5] |
0.5 |
13 |
3.8 |
2.6 |
1.2 |
[-5,55] |
0.6 |
14 |
4 |
3.1 |
1.4 |
[-55,55] |
0.7 |
15 |
1.5 |
3.2 |
1.6 |
[-45,45] |
0.8 |