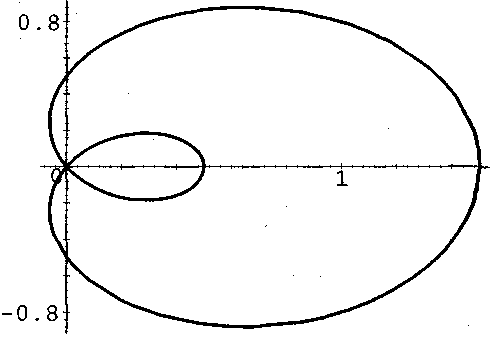- •1. Криволинейный интеграл I рода
- •1.1. Основные понятия
- •1.2. Геометрический и физический смысл криволинейного
- •1.3. Основные свойства криволинейного интеграла I рода
- •1.4. Вычисление криволинейного интеграла I рода
- •1.5. Основные приложения криволинейного
- •2. Криволинейный интеграл II рода
- •2.1. Основные понятия
- •2.2. Физический смысл криволинейного интеграла II рода
- •2.3. Основные свойства криволинейного
- •2.4. Вычисление криволинейного интеграла II рода
- •2.5. Формула Остроградского-Грина
- •2.6. Условия независимости криволинейного
- •2.7. Основные приложения криволинейного
- •3. Индивидуальные задания для контрольной
- •Приложения
- •Составители: е. В. Абрамов, е. Д. Илларионова прямолинейно о криволинейных интегралах
- •404111 Г. Волжский, пр. Ленина, 72
Приложения
Приложение 1
Некоторые кривые на плоскости
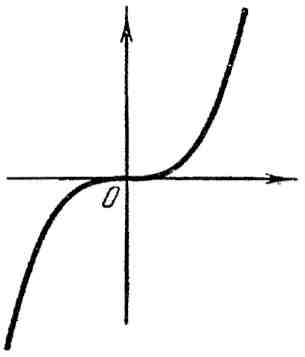
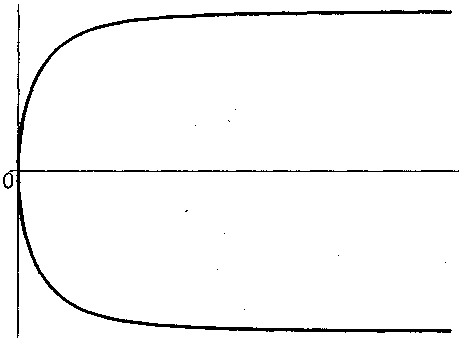
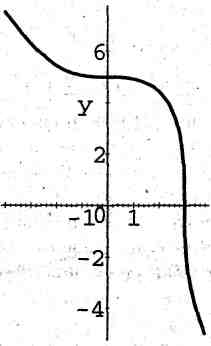
1. Кубическая парабола:
![]() (рис. 1).
(рис. 1).
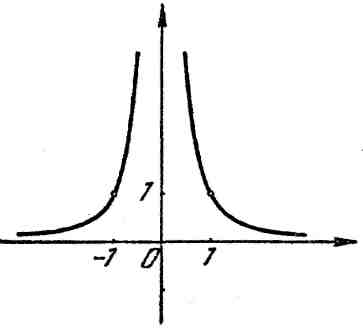
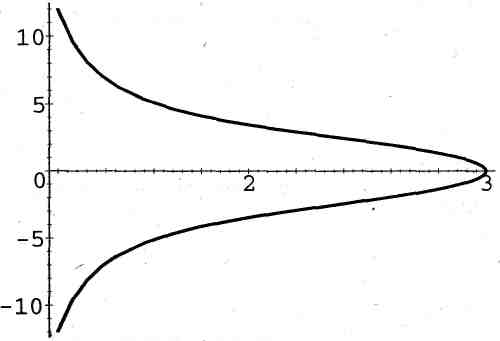
2. Дробная функция:
![]() (рис. 2).
(рис. 2).
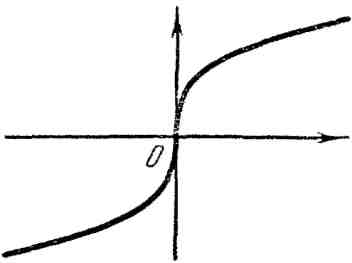
3. Кубическая парабола:
![]() (рис. 3).
(рис. 3).
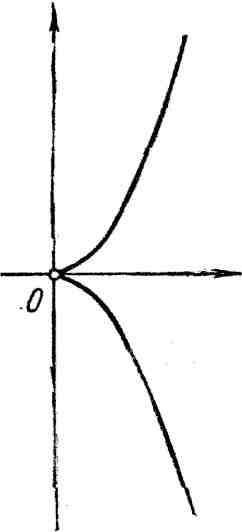
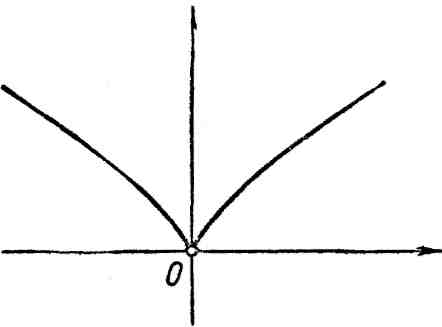
4. Полукубическая парабола:
![]() или
или
![]() (рис. 4).
(рис. 4).
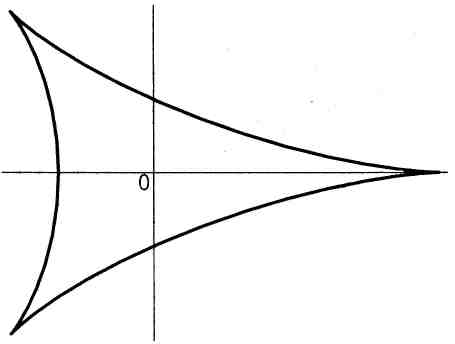
5. Парабола Нейля:
![]() или
или
![]() (рис. 5).
(рис. 5).
|
|
|
|
||
|---|---|---|---|---|---|
|
Рис. 1 |
Рис. 2 |
|
||
|
|
|
|||
Рис. 3 |
Рис. 4 |
Рис. 5 |
|||
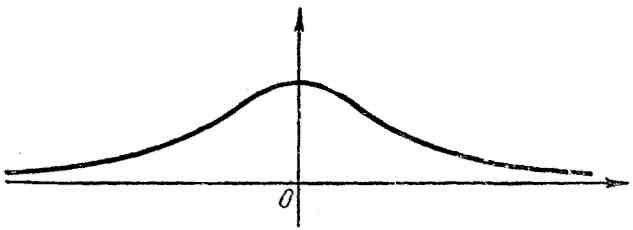
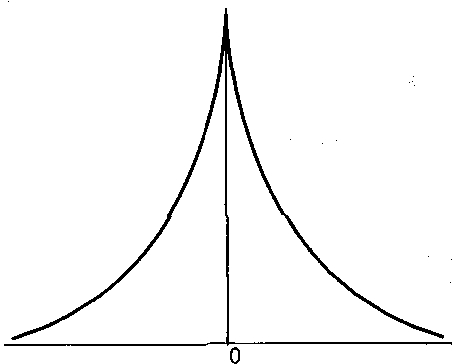
6. Локон Аньези:
![]() (рис. 6).
(рис. 6).
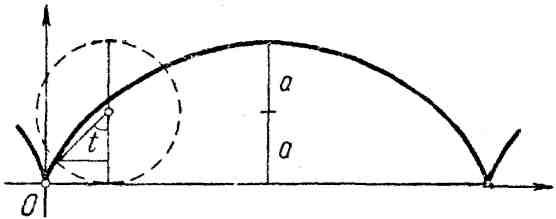
7. Циклоида:
![]() где
где
![]() (рис. 7).
(рис. 7).
8. Циссоида Диоклеса:
![]() или
или
 (рис. 8).
(рис. 8).
|
|
Рис. 6 |
|
|
|
Рис. 7 |
Рис. 8 |
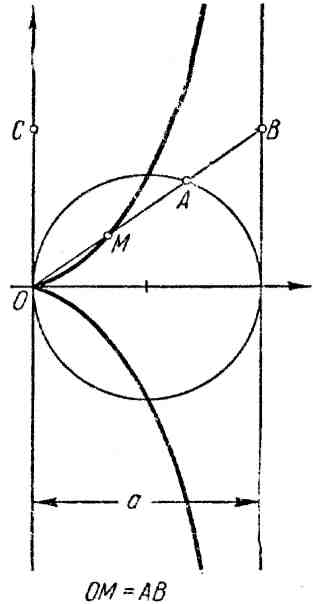
9. Строфоида:
![]() или
или
![]() (рис. 9).
(рис. 9).
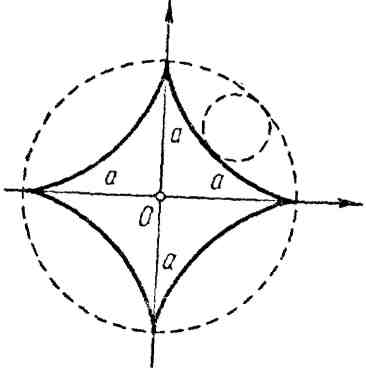
10. Гипоциклоида (астроида):
![]() или
или
![]() где
(рис. 10).
где
(рис. 10).
|
|
Рис. 9 |
Рис. 10 |
11. Эпициклоида:
![]() где
(рис. 11, а – в).
где
(рис. 11, а – в).
|
|
|
а – при
|
б – при
|
в – при
|
Рис. 11
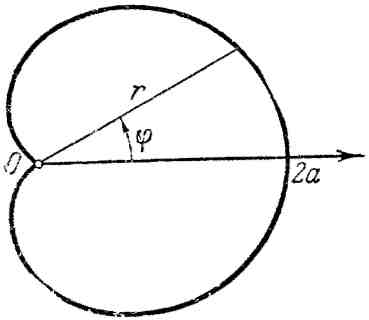
12. Кардиоида:
![]() (рис. 12).
(рис. 12).
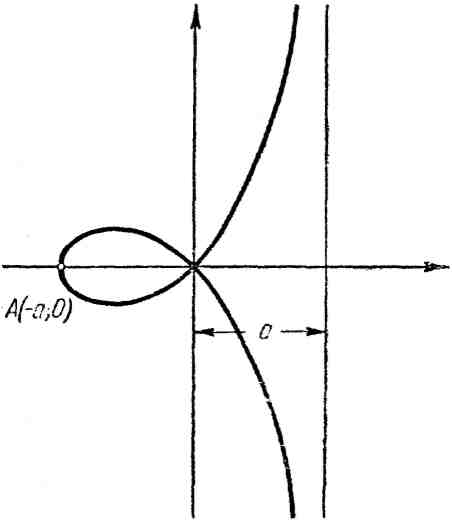
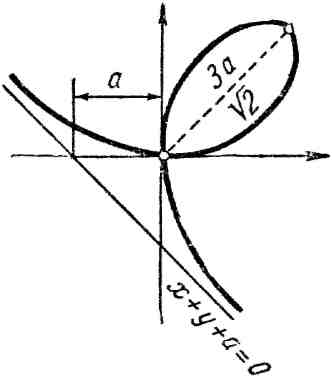
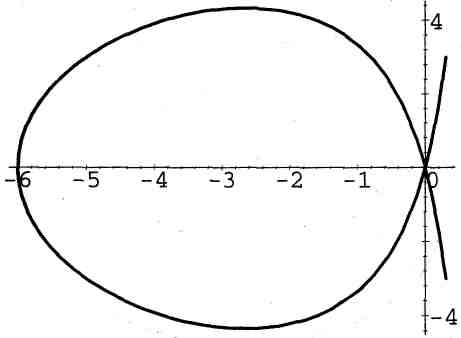
13. Лист Декарта:
![]() или
или
 где
где
![]() или
или
![]() (рис. 13).
(рис. 13).
|
|
Рис. 12 |
Рис. 13 |
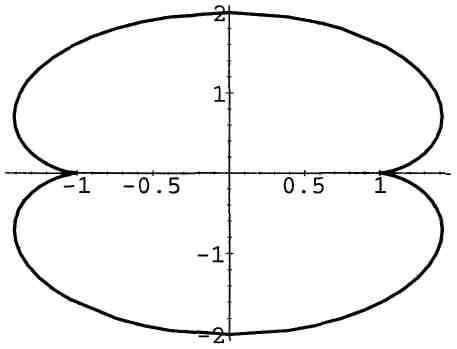
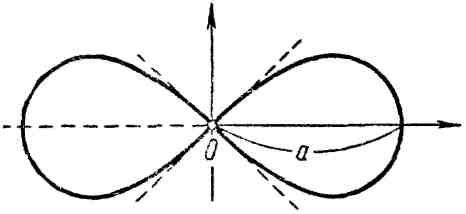
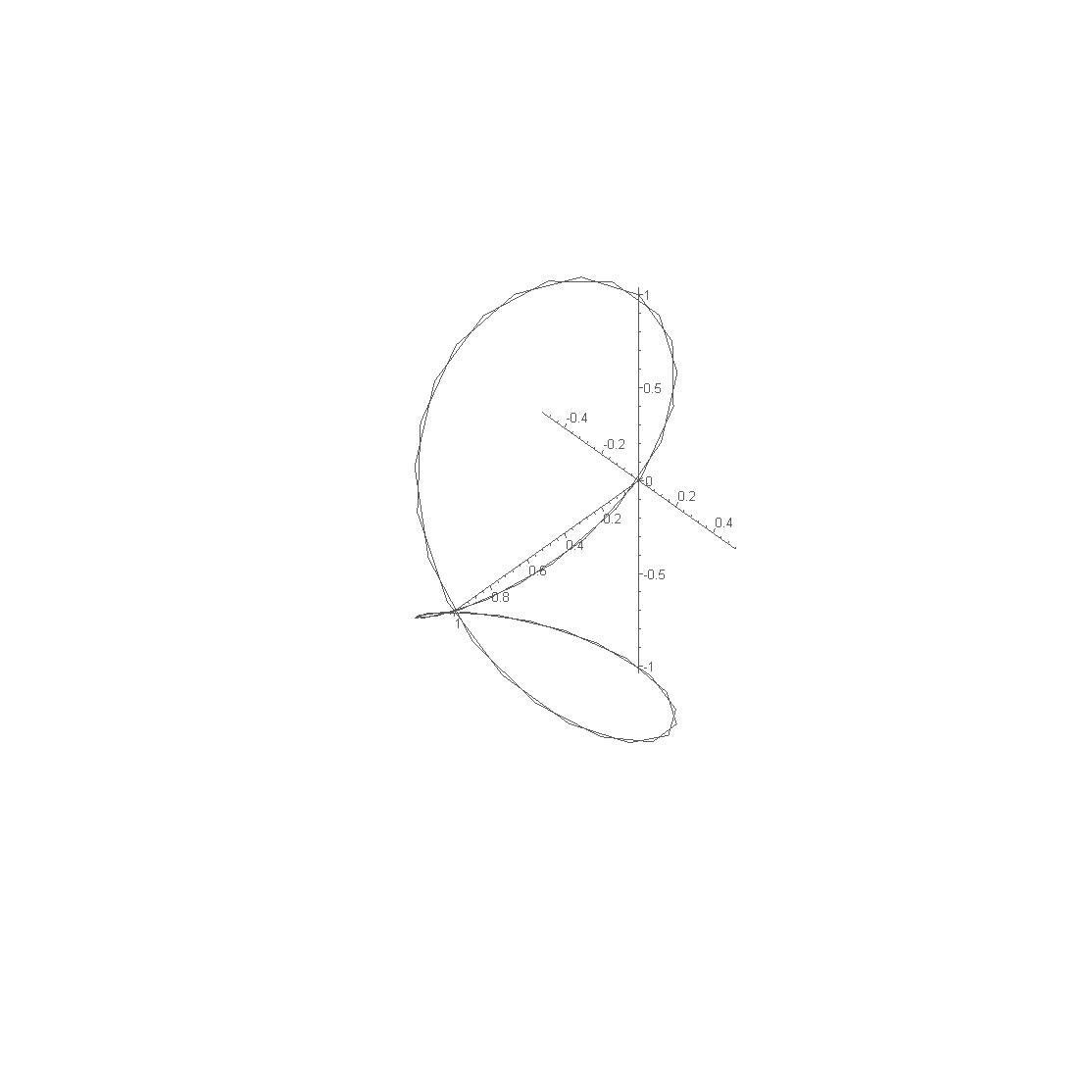
14. Лемниската Бернулли:
![]() или
или
![]() (рис. 14).
(рис. 14).
15. Кривая Штейнера:
 (рис. 15).
(рис. 15).
|
|
Рис. 14 |
Рис. 15 |
16. Трактриса:
 (рис. 16).
(рис. 16).
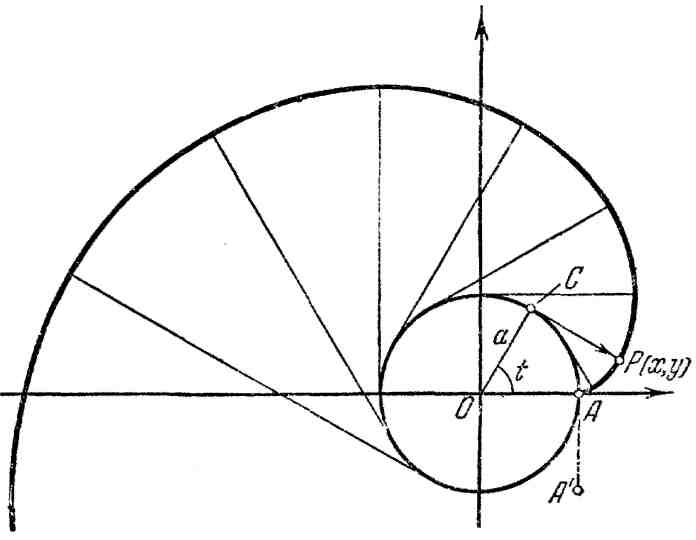
17. Эвольвента (развертка) окружности:
![]() (рис. 17).
(рис. 17).
|
|
Рис. 16 |
Рис. 17 |
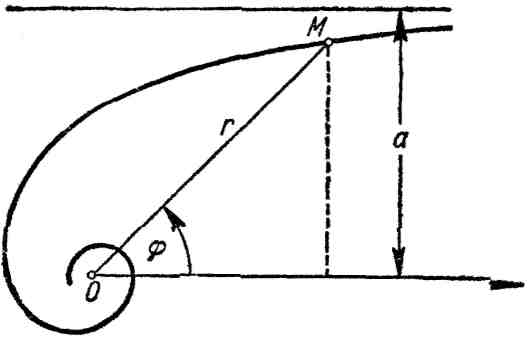
18. Спираль Архимеда:
![]() ,
где
,
где
![]() (рис. 18).
(рис. 18).
19. Гиперболическая спираль:
![]() ,
где
,
где
![]() (рис. 19).
(рис. 19).
|
|
Рис. 18 |
Рис. 19 |
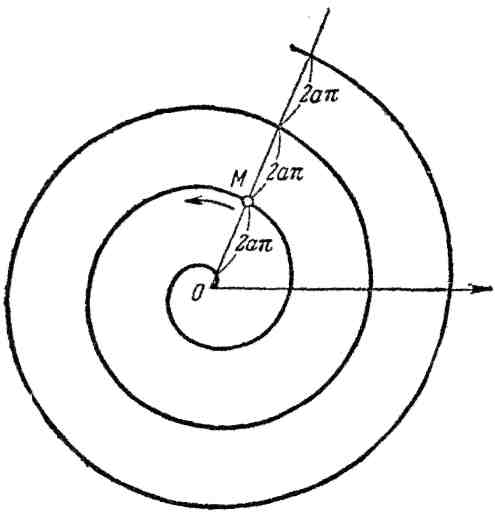
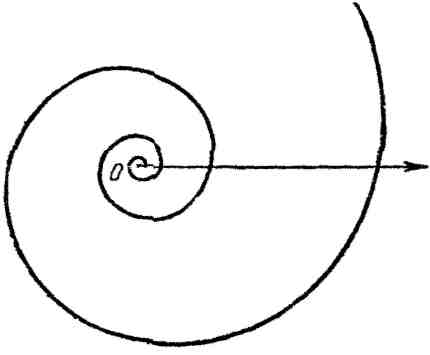
20. Логарифмическая спираль:
![]() (рис. 20).
(рис. 20).
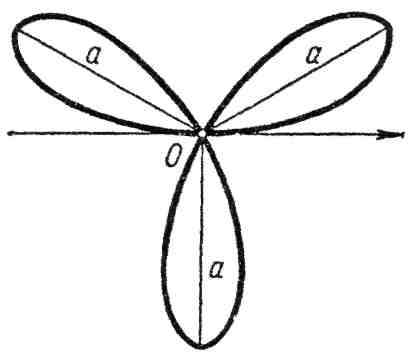
21. Трехлепестковая роза:
![]() ,
где
(рис. 21).
,
где
(рис. 21).
|
|
Рис. 20 |
Рис. 21 |
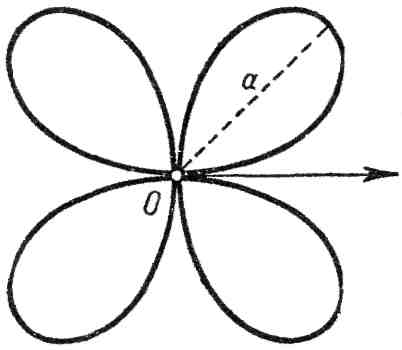
22. Четырехлепестковая роза:
![]() (рис. 22).
(рис. 22).
23. Кривая каппа:
![]() (рис. 23).
(рис. 23).
|
|
Рис. 22 |
Рис. 23 |
24. Конхоида Никомеда:
![]() (рис. 24, а – б).
(рис. 24, а – б).
|
|
а – при
|
б – при
,
|
Рис. 24
25. «Жезл»:
![]() (рис. 25).
(рис. 25).
-

Рис. 25
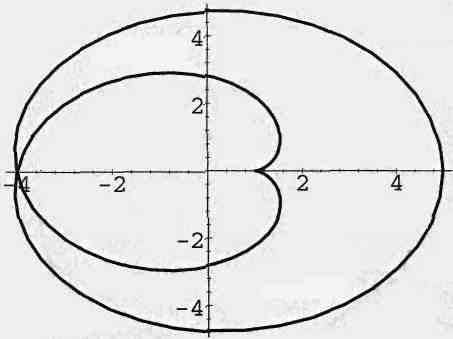
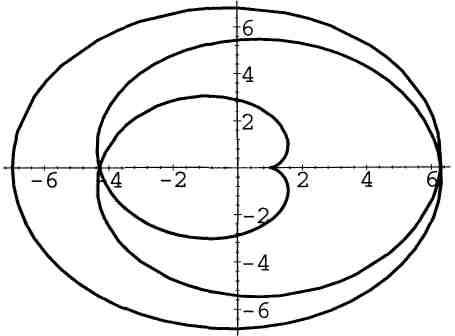
26. Улитка:
![]() (рис. 26, а – б).
(рис. 26, а – б).
|
|
а – при
,
|
б – при
,
|
Рис. 26 |
|
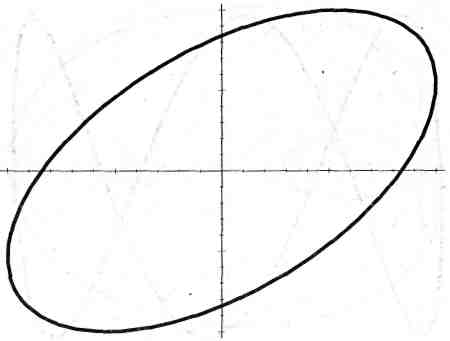
27. Фигуры Лиссажу:
![]() (рис. 27, а),
(рис. 27, а),
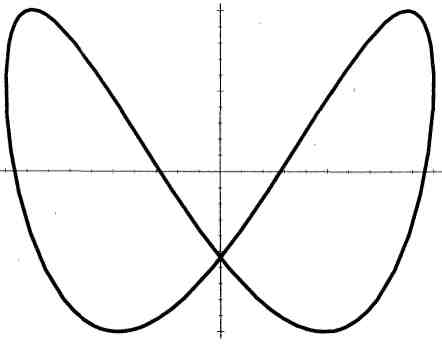
![]() (рис. 27, б),
(рис. 27, б),
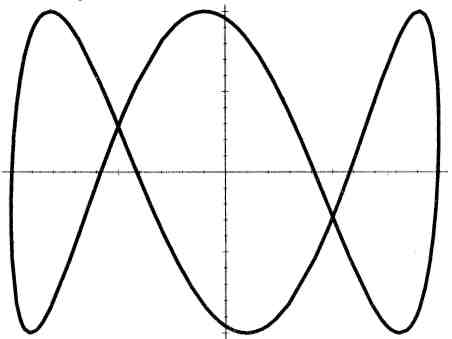
![]() (рис. 27, в).
(рис. 27, в).
|
|
а |
б |
|
|
|
в |
Рис. 27
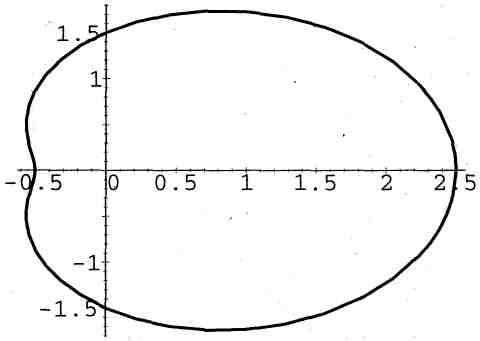
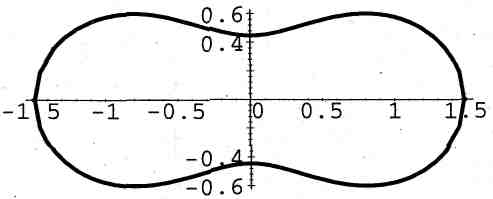
28. Овал Кассини:
![]() ,
где
,
,
где
,
![]() (рис. 28).
(рис. 28).
29. Кривая Ламе:
![]() (рис. 29).
(рис. 29).
|
|
Рис. 28. При
|
Рис. 29. При
,
|
Приложение 2
КРИВЫЕ ВТОРОГО ПОРЯДКА
1. Каноническое
уравнение окружности с центром в точке
![]() и радиуса
:
и радиуса
:
![]() (рис. 1).
(рис. 1).
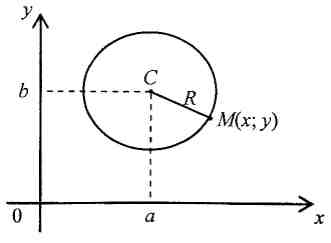
Рис. 1
2. Парабола:
![]() (рис.
2).
(рис.
2).

Рис. 2
3. Каноническое уравнение эллипса:
![]() (рис. 3).
(рис. 3).
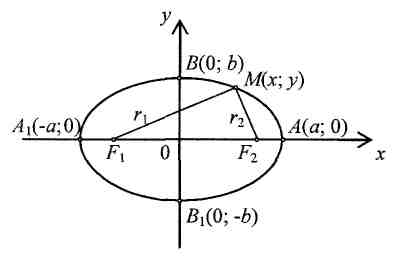
Рис. 3
4. Каноническое уравнение гиперболы:
![]() (рис. 4).
(рис. 4).
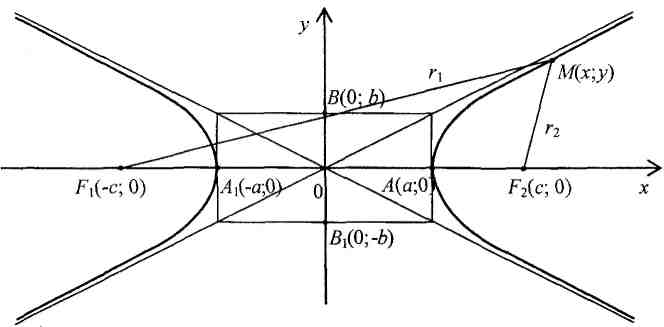
Рис. 4
Приложение 3
Некоторые пространственные кривые
1. Винтовая линия:
 (рис. 1).
(рис. 1).
2. Кривая Вивиани:
 (рис. 2).
(рис. 2).
|
|
Рис. 1. При
,
|
Рис. 2. При
|
Приложение 4
Поверхности второго порядка
1. Каноническое уравнение эллиптического
цилиндра:
![]() (рис. 1). Если
(рис. 1). Если
![]() ,
то
,
то
![]() – прямой круговой цилиндр.
– прямой круговой цилиндр.
2. Каноническое уравнение гиперболического цилиндра:
![]() (рис. 2).
(рис. 2).
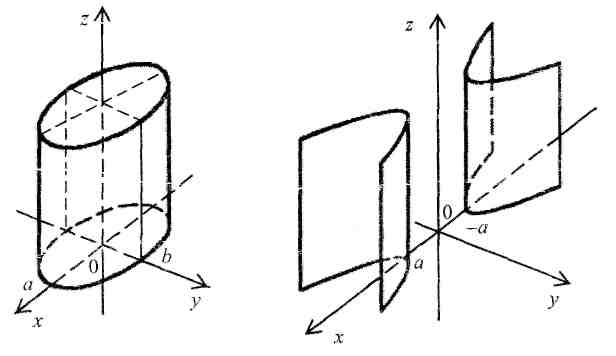
Рис. 1 Рис. 2
3. Каноническое уравнение параболического
цилиндра:
![]() (рис. 3).
(рис. 3).
4. Каноническое уравнение конуса второго порядка:
![]() (рис. 4). Если
,
то
(рис. 4). Если
,
то
![]() – прямой круговой конус.
– прямой круговой конус.
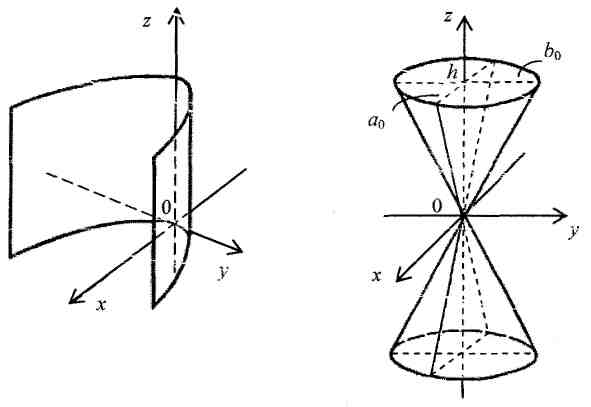
Рис. 3 Рис. 4
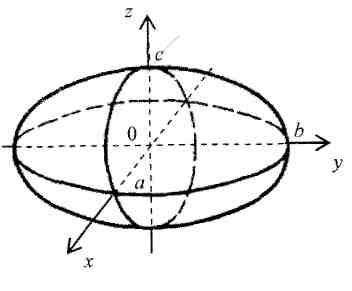
5. Каноническое уравнение эллипсоида:
![]() (рис. 5). Если
(рис. 5). Если
![]() ,
то
,
то
![]() – сфера.
– сфера.
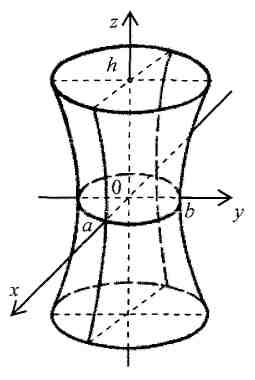
6. Каноническое уравнение однополостного гиперболоида:
![]() (рис. 6). Если
,
то
(рис. 6). Если
,
то
![]() – однополостный гиперболоид вращения.
– однополостный гиперболоид вращения.
Рис. 5 |
Рис. 6 |
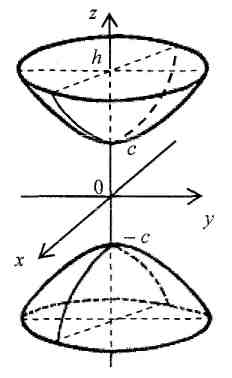
7. Каноническое уравнение двуполостного гиперболоида:
![]() (рис. 7). Если
,
то
(рис. 7). Если
,
то
![]() – двуполостный гиперболоид вращения.
– двуполостный гиперболоид вращения.
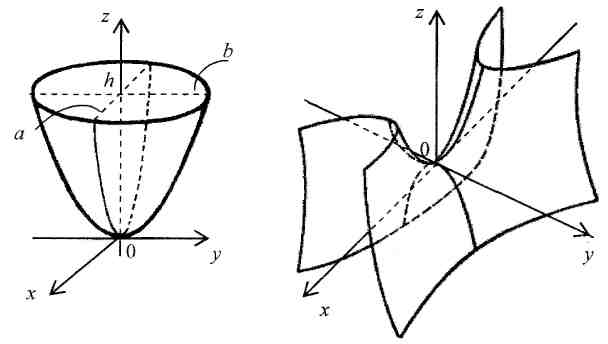
8. Каноническое уравнение эллиптического параболоида
![]() (рис. 8). Если
(рис. 8). Если
![]() ,
то
,
то
![]() – параболоид вращения.
– параболоид вращения.
9. Каноническое уравнение гиперболического параболоида:
![]() (рис. 9).
(рис. 9).
Рис. 7 |
Рис. 8 Рис. 9 |
Содержание
1. Криволинейный интеграл I рода…………………………………….. |
3 |
1.1. Основные понятия……………………………………………….. |
3 |
1.2. Геометрический и физический смысл криволинейного интеграла I рода………………………………………………………... |
4 |
1.3. Основные свойства криволинейного интеграла I рода………… |
5 |
1.4. Вычисление криволинейного интеграла I рода………………… |
6 |
1.5. Основные приложения криволинейного интеграла I рода…….. |
12 |
2. Криволинейный интеграл II рода…………………………………… |
24 |
2.1. Основные понятия……………………………………………….. |
24 |
2.2. Физический смысл криволинейного интеграла II рода……….. |
25 |
2.3. Основные свойства криволинейного интеграла II рода……….. |
27 |
2.4. Вычисление криволинейного интеграла II рода……………….. |
27 |
2.5. Формула Остроградского-Грина………………………………… |
34 |
2.6. Условия независимости криволинейного интеграла II рода от пути интегрирования……………………………………………… |
37 |
2.7. Основные приложения криволинейного интеграла II рода…… |
42 |
3. Индивидуальные задания для контрольной работы……………….. |
45 |
Список литературы……………………………………………………… |
47 |
Приложения……………………………………………………………… |
48 |
План уч.-метод. докум. 2008 г., поз. № 27