2.7. Основные приложения криволинейного
интеграла II рода
Площадь плоской фигуры
Из теоремы 2.2 следует, что если в
формуле Остроградского-Грина (2.19)
подобрать функции
и
так, чтобы
,
то, как известно, двойной интеграл в
формуле (2.19) будет определять площадь
области
,
т. е. можно получить бесконечно много
формул вида
,
где
– площадь области
.
В частности, можно положить
и
или
и
.
В обоих случаях получим:
и
.
(2.30)
Складывая почленно эти равенства, будем иметь:
.
(2.31)
Таким образом, площадь плоской области , расположенной в плоскости и ограниченной замкнутой кривой , можно найти с помощью криволинейного интеграла II рода по формуле (2.31), при этом обход кривой выполняется в положительном направлении (правило, п. 2.3).
Замечания
1. Подынтегральное выражение в формуле
(2.31) легко запомнить, если его записать
в виде определителя 2-го порядка
.
2. Формула (2.31) наиболее удобна и часто используется при решении задач.
Пример 7. Вычислить площадь фигуры,
ограниченной петлей кривой
(рис. 2.8).
Решение. Перейдем к параметрическим
уравнениям данной кривой, положив
.
Подставив
в исходное уравнение кривой, получим
,
т. е
,
тогда
.
Петля замыкается в точке с абсциссой
,
откуда находим
.
Искомую площадь определим по формуле
(2.30), где рассуждения проведем, используя
формулу (2.9). Так как
и
,
то получим:
.
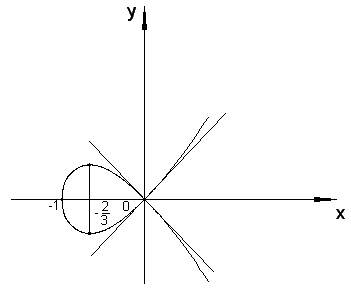
Рис. 2.8
Ответ: 
кв. ед.
Работа переменной силы.
Как отмечалось ранее (п. 2.2), переменная
сила
на криволинейном участке
производит работу, которая находится
по формуле (2.5):
.
Если сила
задана по пространственной кривой
,
то работа вычисляется по формуле (2.6):
.
Пример 8. Вычислить работу силы
вдоль дуги параболы
,
заключенной между точками
и
.
Решение. По формуле (2.5) получим:
.
Воспользуемся формулой (2.13):
.
Ответ: 
Дж.
Самостоятельная работа
1. С помощью криволинейного интеграла II рода найти площадь фигур, ограниченных линиями:
а) первой аркой циклоиды и осью ;
б) астроидой
в) эллипсом ;
г) кардиоидой
д) лемнискатой Бернулли
;
е) и .
2. Вычислить работу силы
,
совершаемую по прямой от точки
до точки
.
3. Вычислить работу силы
при перемещении материальной точки по
прямой
от точки
до точки
.
4. Вычислить работу силы
при перемещении материальной точки
вдоль контура квадрата , образованного
прямыми
,
.
5. Вычислить работу силы
при перемещении материальной точки
вдоль окружности
по ходу часовой стрелки.
6. Вычислить работу силы
вдоль отрезка прямой
,
если
и
.
3. Индивидуальные задания для контрольной
работы
1. Вычислить работу силы при перемещении точки вдоль дуги линии :
1) 
,
,
расположенная во втором координатном
углу, в направлении против часовой
стрелки.
2) 
,
в направлении против часовой стрелки.
3) 
,
от точки
до точки
.
4) 
,
в направлении против часовой стрелки.
5) 
,
от точки
до точки
.
6) 
,
в направлении против часовой стрелки.
7) 
,
от точки
до точки
.
8) 
,
в направлении против часовой стрелки.
9) 
,
от точки
до точки
.
10) 
,
,
расположенная в первой координатной
четверти, в направлении против часовой
стрелки.
2. Показать, что данное выражение является полным дифференциалом функции . Найти функцию .
1) 
;
2) 
;
3) 
;
4) 
;
5) 
;
6) 
;
7) 
;
8) 
;
9) 
;
10) 
.
Список литературы
1. Выгодский, М. Я. Справочник по высшей математике / М. Я. Выгодский. – М. : АСТ: Астрель, 2006. – 991 с.
2. Каплан, И. А. Практические занятия по высшей математике. Ч. IV / И. А. Каплан. – Харьков : Из-во Гос. ун-та им. А. М. Горького, 1966. – 236 с.
3. Кратные и криволинейные интегралы : методич. указ. / Сост. В. А. Меркулов. – Волгоград : ВолгИСИ, 1992. – 46 с.
4. Лунгу, К. Н. Сборник задач по высшей математике. 2 курс / К. Н. Лунгу [и др.] ; под ред. С. Н. Федина. – М. : Айрис-пресс, 2004. – 592 с. : ил. – (Высшее образование).
5. Меркулов, В. А. Курс высшей математики. Избранные разделы. Раздел 1 : Аналитическая геометрия : учеб. пособие / В. А. Меркулов. – Волгоград, 2004. – 88 с.
6. Письменный, Д. Т. Конспект лекций по высшей математике. Ч. 2 / Д. Т. Письменный. – М.: Рольф, 2001. – 256 с.
7. Рябушко, А. П. Сборник индивидуальных заданий по высшей математике. В 3-х ч. Ч. III / А. П. Рябушко [и др.]. – Минск : Вышэйшая школа, 1991. – 288 с.