
- •1. Криволинейный интеграл I рода
- •1.1. Основные понятия
- •1.2. Геометрический и физический смысл криволинейного
- •1.3. Основные свойства криволинейного интеграла I рода
- •1.4. Вычисление криволинейного интеграла I рода
- •1.5. Основные приложения криволинейного
- •2. Криволинейный интеграл II рода
- •2.1. Основные понятия
- •2.2. Физический смысл криволинейного интеграла II рода
- •2.3. Основные свойства криволинейного
- •2.4. Вычисление криволинейного интеграла II рода
- •2.5. Формула Остроградского-Грина
- •2.6. Условия независимости криволинейного
- •2.7. Основные приложения криволинейного
- •3. Индивидуальные задания для контрольной
- •Приложения
- •Составители: е. В. Абрамов, е. Д. Илларионова прямолинейно о криволинейных интегралах
- •404111 Г. Волжский, пр. Ленина, 72
2.6. Условия независимости криволинейного
интеграла II рода от пути интегрирования
Пусть
![]() и
и
![]() – две произвольные точки односвязной
области
плоскости
.
Точки
и
можно соединить различными линиями. По
каждой из этих кривых интеграл
– две произвольные точки односвязной
области
плоскости
.
Точки
и
можно соединить различными линиями. По
каждой из этих кривых интеграл
![]() имеет различные значения. Если же его
значения по всевозможным кривым
одинаковы, то говорят, что интеграл не
зависит от пути интегрирования. В этом
случае для интеграла достаточно отметить
лишь его начальную точку
и его конечную точку
пути. Такой интеграл обозначают:
имеет различные значения. Если же его
значения по всевозможным кривым
одинаковы, то говорят, что интеграл не
зависит от пути интегрирования. В этом
случае для интеграла достаточно отметить
лишь его начальную точку
и его конечную точку
пути. Такой интеграл обозначают:
 .
(2.20)
.
(2.20)
Сформулируем в виде теоремы без доказательства условия, при которых криволинейный интеграл II рода не зависит от пути интегрирования.
Теорема 2.3 (признак независимости криволинейный интеграл II рода от пути интегрирования). Для того, чтобы криволинейный интеграл II рода не зависел от пути интегрирования в односвязной области , в которой функции и непрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие:
![]() .
(2.21)
.
(2.21)
Пример 5. Вычислить
 .
.
Решение. Так как
![]() ,
а
,
а
![]() ,
то
,
то
![]() и
и
![]() ,
тогда
.
Следовательно, по теореме 2.3 можно
выбрать любой удобный путь интегрирования.
От точки
,
тогда
.
Следовательно, по теореме 2.3 можно
выбрать любой удобный путь интегрирования.
От точки
![]() к точке
к точке
![]() будем двигаться по отрезкам, параллельным
координатным осям (рис. 2.7), так как
вычисление исходного интеграла в этом
случае самое простое (п. 2.4).
будем двигаться по отрезкам, параллельным
координатным осям (рис. 2.7), так как
вычисление исходного интеграла в этом
случае самое простое (п. 2.4).
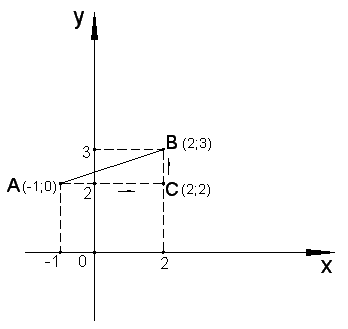
Рис. 2.7
Следовательно, по свойству 4 криволинейного интеграла II рода
(п. 2.3) имеем
![]() .
Так как отрезок
.
Так как отрезок
![]() задается уравнением
задается уравнением
![]() ,
то
,
а
,
то
,
а
![]() ,
поэтому
,
поэтому
![]() .
Так как отрезок
задается уравнением
.
Так как отрезок
задается уравнением
![]() ,
то
,
а
,
то
,
а
![]() ,
тогда
,
тогда
![]() .
Окончательно имеем:
.
Окончательно имеем:
![]() .
.
Ответ: ![]() .
.
Рассмотрим еще две теоремы.
Терема 2.4. Если выполняется
условие (2.21), то подынтегральное выражение
![]() является полным дифференциалом некоторой
функции
является полным дифференциалом некоторой
функции
![]() ,
т. е. имеет место равенство:
,
т. е. имеет место равенство:
![]() .
(2.22)
.
(2.22)
Тогда из равенства (2.22), согласно (2.20) и свойства определенного интеграла, получим:
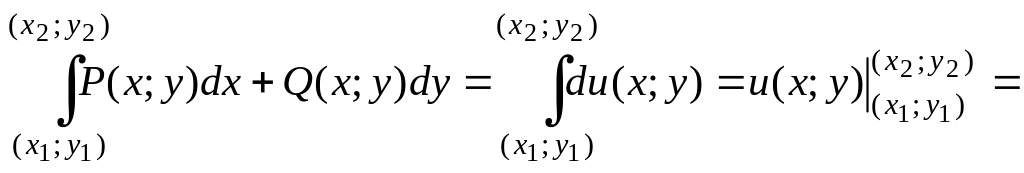
![]() ,
,
т. е.
 .
(2.23)
.
(2.23)
Формула (2.23) называется обобщенной формулой Ньютона-Лейб-ница для криволинейного интеграла II рода от полного дифференциала.
Теорема 2.5. Если подынтегральное
выражение
![]() +
+
![]() есть полный дифференциал и путь
интегрирования
– замкнутая кривая, то
есть полный дифференциал и путь
интегрирования
– замкнутая кривая, то
![]() .
(2.24)
.
(2.24)
Замечания
1. Утверждения, сформулированные в теоремах 2.3 – 2.5, равно-
сильны между собой, то есть, выполнение любого из них влечет за собой выполнение остальных.
2. Чтобы не путать переменную
интегрирования
с верхним пределом
,
переменную интегрирования договоримся
обозначать другой буквой (например,
,
,
![]() и т. д.).
и т. д.).
3. Функцию , удовлетворяющую условию (2.21), можно найти, используя формулу:
 .
(2.25)
.
(2.25)
В качестве начальной точки
![]() обычно берут начало координат
обычно берут начало координат
![]() .
.
4. Аналогичные результаты справедливы
для криволинейного интеграла II
рода
![]() по пространственной кривой
.
Условие (2.21), равенство (2.22), формулы
(2.23) и (2.25) имеют соответственно вид:
по пространственной кривой
.
Условие (2.21), равенство (2.22), формулы
(2.23) и (2.25) имеют соответственно вид:
,
![]() ,
,
![]() ,
(2.26)
,
(2.26)
![]() ,
(2.27)
,
(2.27)
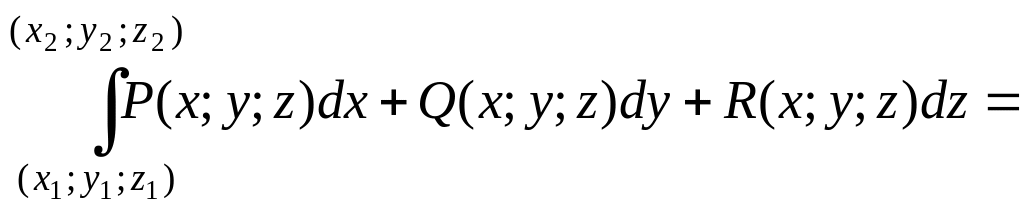
![]() ,
(2.28)
,
(2.28)
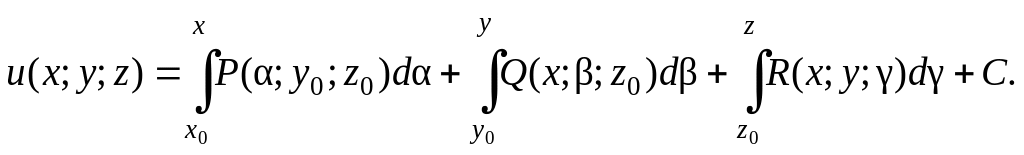 (2.29)
(2.29)
Пример 6. Показать, что выражение
![]() является полным дифференциалом функции
.
Найти функцию
.
является полным дифференциалом функции
.
Найти функцию
.
Решение. Проверим выполнимость
условия (2.21). Так как
![]() ,
то
,
то
![]() и так как
и так как
![]() ,
то
,
то
![]() .
Следовательно, условие (2.21) выполняется
и по теореме 2.4 исходное выражение
является дифференциалом некоторой
функции
.
Найдем ее по формуле (2.25).
.
Следовательно, условие (2.21) выполняется
и по теореме 2.4 исходное выражение
является дифференциалом некоторой
функции
.
Найдем ее по формуле (2.25).
Пусть
![]() и
и
![]() ,
тогда:
,
тогда:
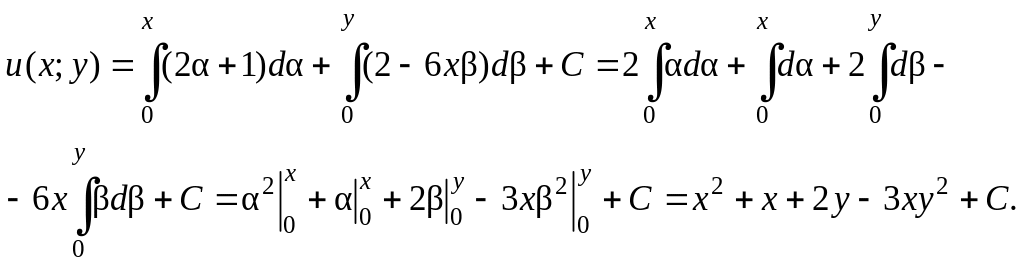
Ответ: ![]() .
.
Самостоятельная работа
1. Вычислить:
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 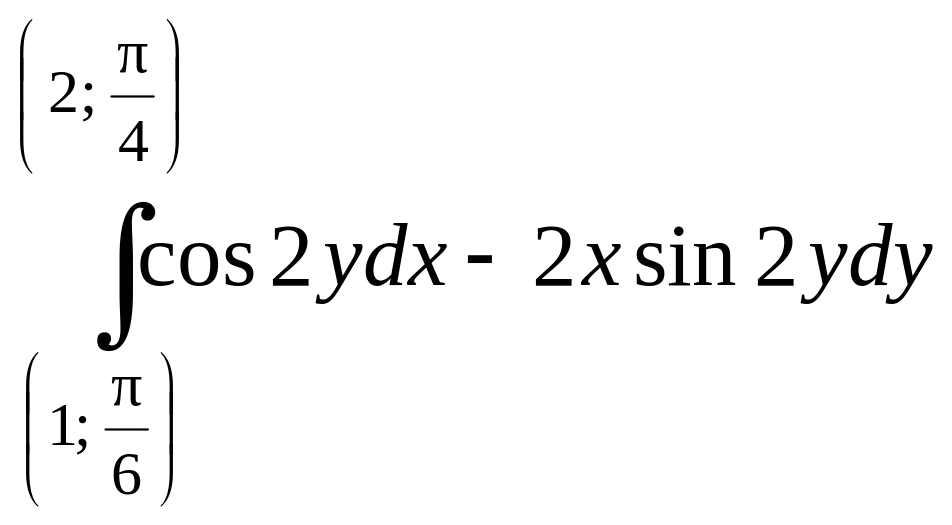 ;
;
д) 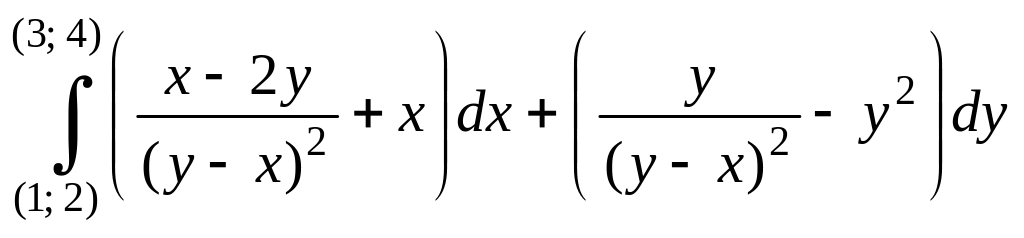 ;
;
е)  ; ж)
; ж) 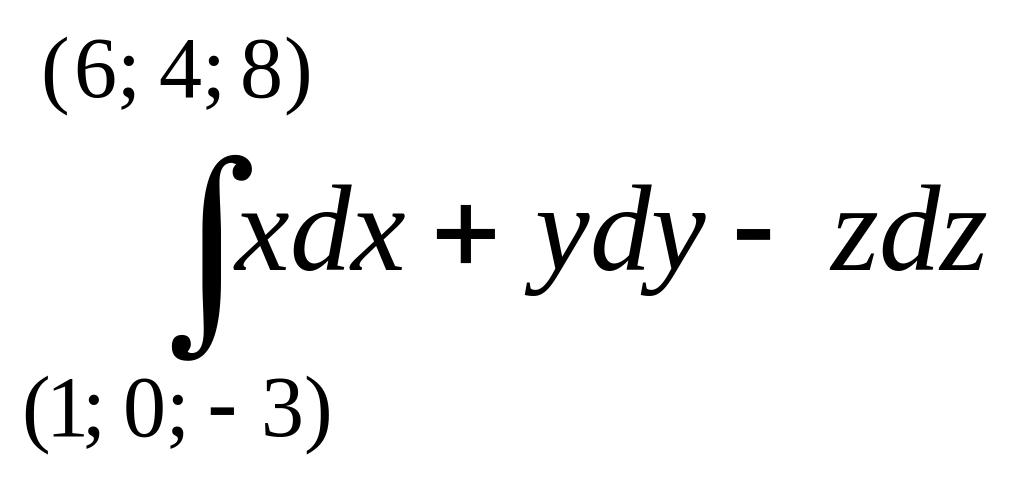 .
.
2. Показать, что данное выражение является полным дифференциалом некоторой функции . Найти эту функцию с помощью криволинейного интеграла II рода.
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]() ;
д)
;
д) ![]() ;
;
е)  .
.
