2.5. Формула Остроградского-Грина
Связь между двойным интегралом по
области
и криволинейным интегралом II
рода по границе
этой области устанавливает формула
Остроградского-Грина, которая имеет
широкое применение в математике.
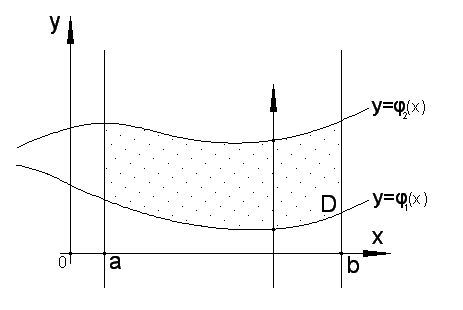
Пусть на плоскости задана область , являющаяся областью I или II типа.
Область, ограниченная слева и справа
прямыми
,
(
),
а снизу и сверху линиями
,
(
)
называется областью I
типа (правильной в направлении оси
)
(рис. 2.5, а). При этом любая
прямая, параллельная оси
и пересекающая область снизу вверх
имеет одну и туже границу входа
в область и одну и туже границу выхода
из нее.
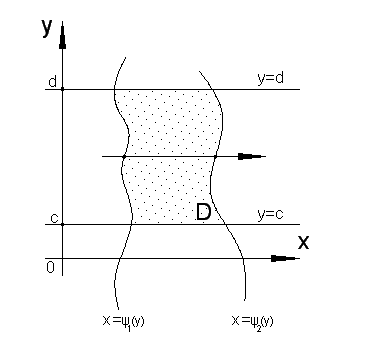
Область, ограниченная снизу и сверху
прямыми
,
(
),
а слева и справа линиями
,
(
)
называется областью II
типа (правильной в направлении оси
)
(рис. 2.5, б). При этом любая
прямая, параллельная оси
и пересекающая область слева направо
имеет одну и туже границу входа
в область и одну и туже границу выхода
из области.
а |
|
|
б |
Рис. 2.5
Теорема 2.2. Если функции
и
непрерывны вместе со своими частными
производными
и
в замкнутой односвязной2
области
,
то имеет место формула
,
(2.19)
которая называется формулой Остроградского-Грина, где граница области – кусочно-гладкая кривая и интегрирование вдоль кривой производится в положительном направлении (правило, п. 2.3).
Замечания
1. Формула (2.19) справедлива и для произвольной области . В этом случае область разбивают на части, каждая из которых является областью I или II типа и к каждой из этих частей применяют формулу (2.19), а полученные результаты суммируют.
2. Во многих случаях использование формулы (2.19) ведет к упрощению решения задачи.
Пример 4. Применив формулу
Остроградского-Грина, вычислить
,
где
– контур треугольника
с вершинами в точках
,
и
.
Решение. Воспользуемся формулой (2.19). Выполним чертеж области в плоскости (рис. 2.6). Область является областью I и II типа одновременно. Договоримся рассматривать область как область I типа.
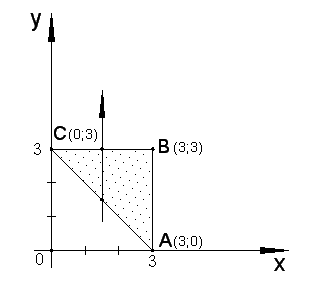
Рис. 2.6
По условию
и
,
тогда
и
.
Следовательно,
=
.
Способ представления двойного интеграла
в виде повторного известен (
– область I типа). Найдем
пределы интегрирования. Если провести
произвольную прямую, параллельную оси
и пересекающую область
,
то видно, что границей входа этой прямой
в область является сторона
,
а границей выхода – сторона
.
Тем самым мы нашли нижний и верхний
пределы интегрирования по переменной
для внутреннего интеграла в повторном:
.
Проектируя треугольник
на ось
,
видно, что
.
Таким образом, получим:
.
Вычислим внутренний интеграл в
предположении, что
– постоянная величина:
.
От полученной функции вычислим внешний
интеграл:
.
Ответ: 
.
Самостоятельная работа
С помощью формулы Остроградского-Грина вычислить:
1. 
,
если
– контур треугольника со сторонами
,
и
.
2. 
,
где
состоит из дуги параболы
,
соединяющей точки
и
и отрезка прямой, соединяющего эти
точки.
3. 
,
где контур
– эллипс
.
4. 
,
где
– контур прямоугольника с вершинами
,
,
и
.
5. 
,
где контур
– окружность
,
«пробегаемая» в положительном направлении
обхода.