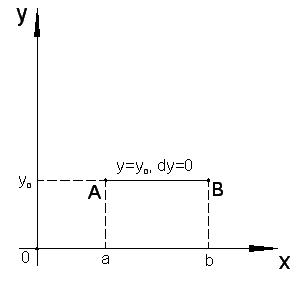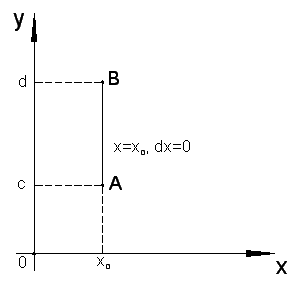2.3. Основные свойства криволинейного

интеграла II рода

Рассмотрим основные свойства криволинейного интеграла II рода без доказательств, которые обобщают соответствующие свойства определенного интеграла. Пусть функции и непрерывны на кривой , тогда:

1. При изменении направления пути интегрирования криволинейный интеграл II рода меняет свой знак на противоположный, т. е. .

2.  ,

где .

3. Если кривую разбить точкой на две части и , то интеграл по всей кривой равен сумме интегралов по ее частям, т. е. .

4. Если кривая лежит в плоскости, перпендикулярной оси , то . Аналогично, если кривая расположена в плоскости, перпендикулярной оси , то .

5. Значение криволинейного интеграла II рода по замкнутой кривой (обозначается ) не зависит от выбора начальной точки, а зависит только от направления обхода кривой.

Правило. Если кривая интегрирования замкнута, то за положительное направление обхода по принимается такое направление, при котором область поверхности, ограниченная кривой , находится слева, если двигаться вдоль по выбранной стороне этой поверхности.

Замечание. Аналогичные свойства выполняются для криволинейного интеграла II рода по пространственной кривой интегрирования .

2.4. Вычисление криволинейного интеграла II рода

Криволинейные интегралы II рода вычисляют, сводя к определенным интегралам.

Параметрическое задание кривой интегрирования

Если кривая на плоскости задана параметрическими уравне-

ниями , где функции и непрерывны вместе со своими производными на отрезке , причем начальной точке кривой соответствует значение параметра , а конечной точке – значение и пусть функции и непрерывны на кривой , тогда имеет место формула для вычисления криволинейного интеграла II рода по координате и соответственно:

; (2.7)

. (2.8)

Складывая почленно равенства (2.7) и (2.8), получим формулу для вычисления криволинейного интеграла II рода общего вида:

. (2.9)

Пример 1. Вычислить , где – окружность при положительном направлении обхода.

 Решение. Воспользуемся формулой (2.9). При параметрическом построении окружности положительным направлением обхода является движение против часовой стрелки, поэтому параметр меняется от 0 до . Выполним необходимые преобразования: , . Получим:

= =

= .

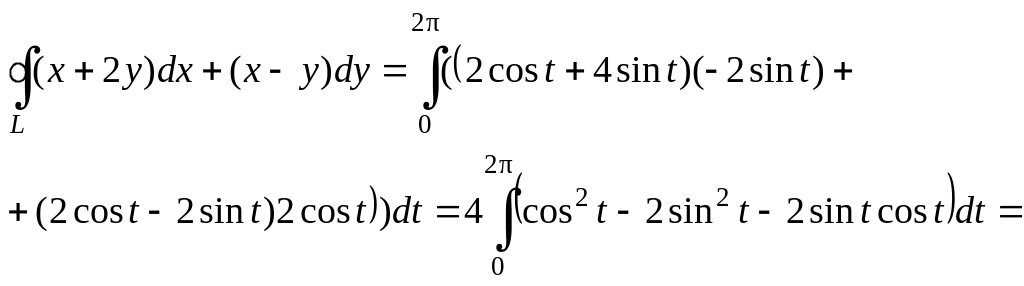
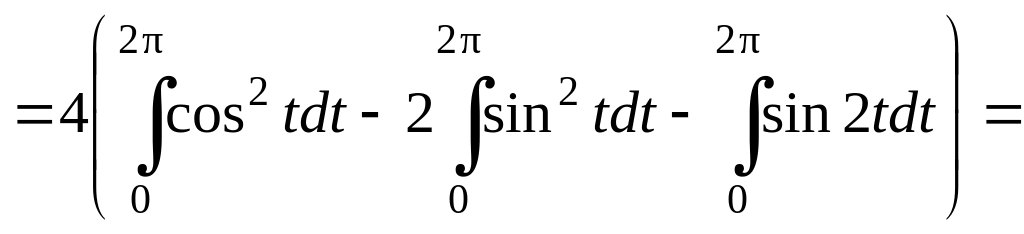
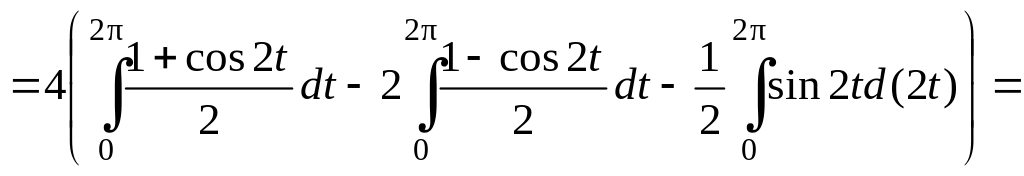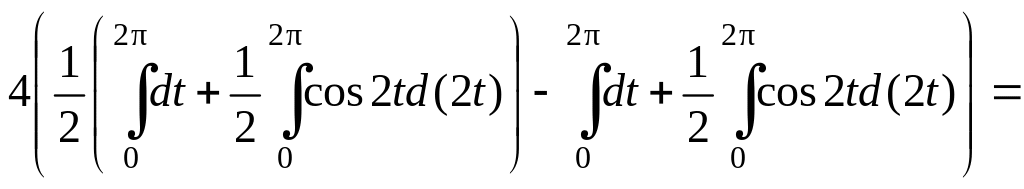
Ответ: . 

Если кривая задана параметрическими уравнениями 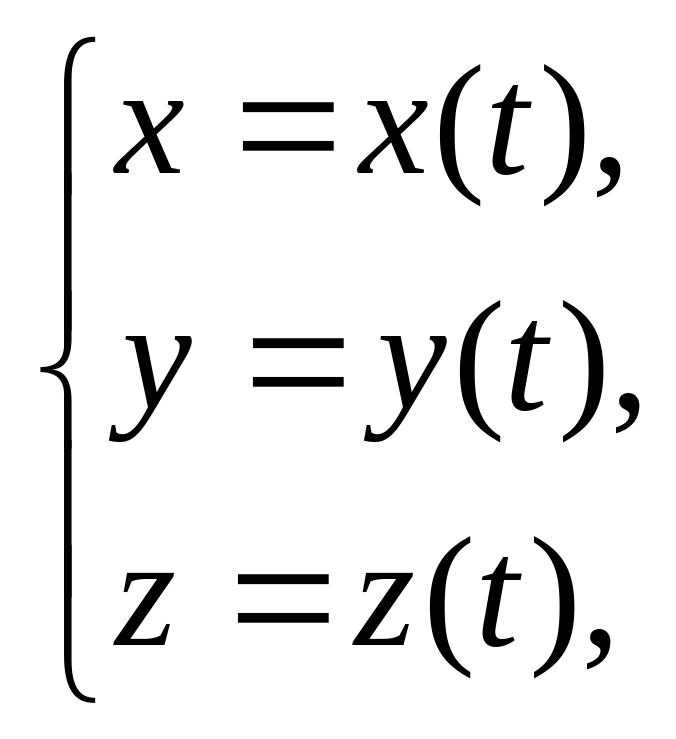в пространстве, где функции , и непрерывны вместе со своими производными на отрезке , причем начальной точке кривой соответствует значение параметра , а конечной точке – значение и функции , и непрерывны на кривой , тогда формула вычисления криволинейного интеграла II рода общего вида по пространственной кривой имеет вид:

(2.10)

Замечание. Применение формулы (2.10) при решении задач аналогично использованию формулы (2.9).

Пример 2. Вычислить , где – отрезок прямой, соединяющий точки и .

 Решение. Запишем параметрические уравнения прямой 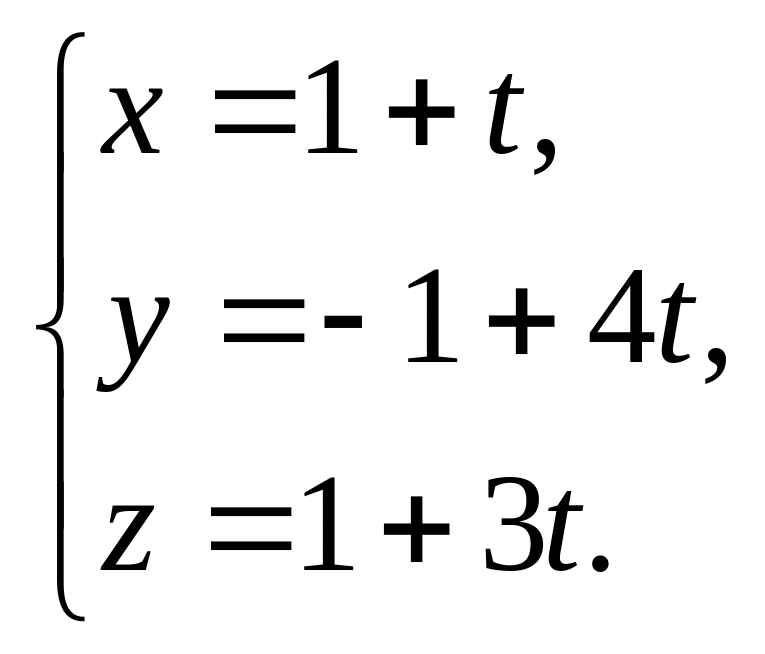Подставляя в уравнение абсциссы точек и видим, что параметр меняется от 0 до 1. Поэтому, согласно формуле (2.10) получим:

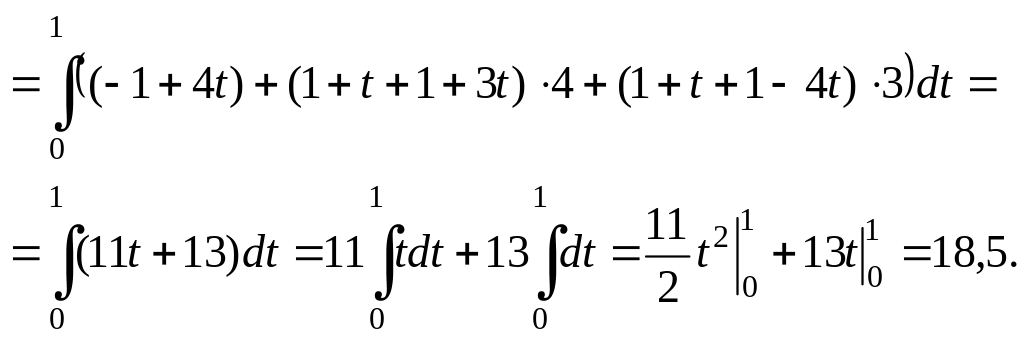
Ответ:  . 

Явное задание кривой

Если кривая задана на плоскости уравнением , , где функция и ее производная непрерывны на отрезке и функции , непрерывны на кривой , тогда имеют место формулы для вычисления криволинейного интеграла II рода по координате и соответственно:

(2.11)

и

. (2.12)

Криволинейный интеграл II рода общего вида по плоской кривой интегрирования вычисляется по следующему правилу:

. (2.13)

Пример 3. Вычислить , где – дуга параболы от точки до точки .

 Решение. Так как дуга параболы расположена в первой координатной четверти, то . Пределы интегрирования известны по условию, тогда по формуле (2.13) получим:

.

Ответ:  . 

Замечания

1. Если кривая определяется уравнением , то формула (2.13) примет вид:

. (2.14).

2. При неявном задании кривой уравнением вычисление проводится по тем же формулам.

Отметим важные частные случаи. Если кривая интегрирования – отрезок прямой, параллельной оси (рис.2.3, а), то криволинейный интеграл II рода сразу превращается в определенный, так как в этом случае и , поэтому

. (2.15)

Аналогично, если кривая – отрезок прямой, параллельной оси (рис. 2.3, б), то , и

. (2.16)

а	б

Рис. 2.3

Если гладкая пространственная кривая задается уравнениями , где функции , и их производные , непрерывны на отрезке и функции , и непрерывны на кривой , тогда криволинейный интеграл II рода общего вида по пространственной кривой равен:

(2.17)

Замечание. Формулы (2.11) – (2.13), (2.17) получаются из формул (2.7) – (2.10) соответственно, если в качестве параметра взять .

Криволинейные интегралы I и II рода связаны равенством:

, (2.18)

где и – углы, составляемые с осями координат направленной касательной к кривой в точке и положительное направление касательной соответствует направлению движения точки по кривой от к (рис. 2.4).

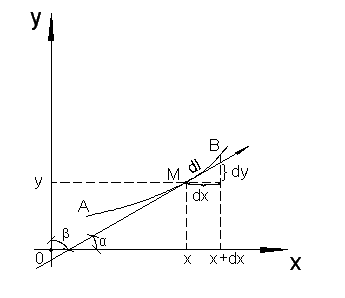
Рис. 2.4

Самостоятельная работа

1. Вычислить , где – дуга эллипса от точки до точки .

2. Вычислить , где – дуга циклоиды .

3. Вычислить , где – верхняя дуга астроиды от точки до точки .

4. Вычислить по петле листа Декарта .

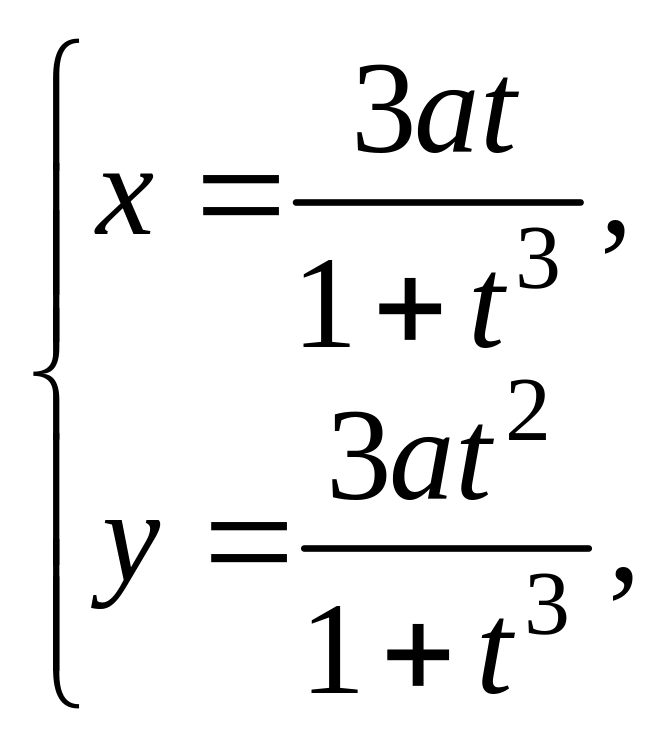
5. Вычислить , где – дуга винтовой линии 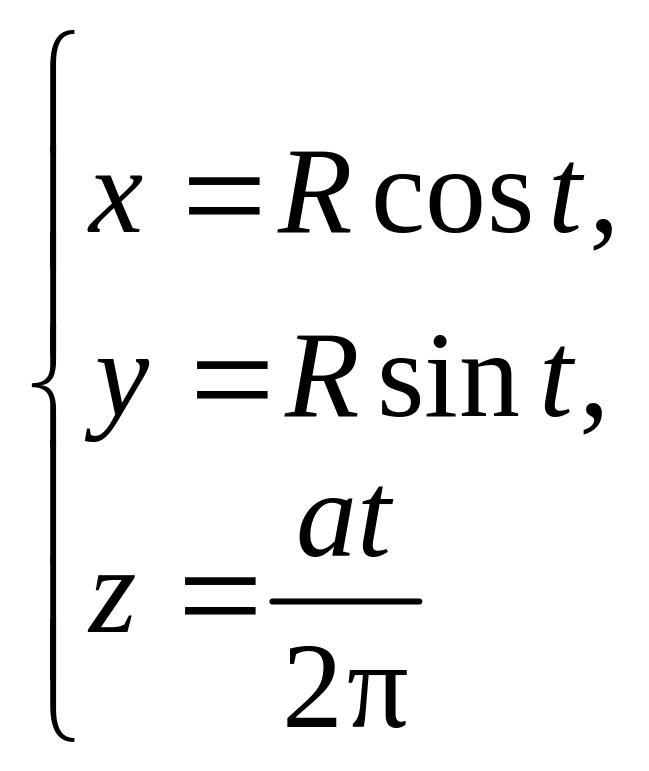от точки пересечения линии с плоскостью до точки ее пересечения с плоскостью .

6. Вычислить , где – дуга одного витка винтовой линии , .

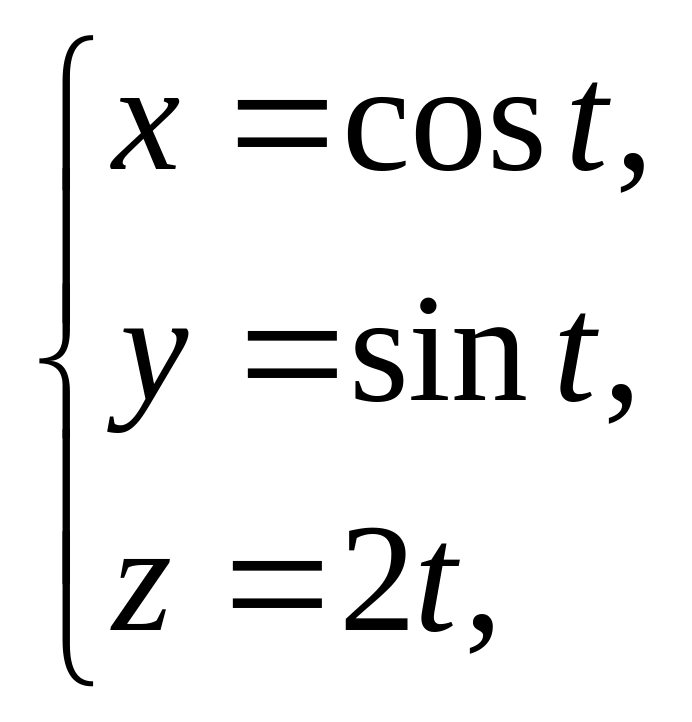
7. Вычислить , где – окружность, заданная формулами ( ).

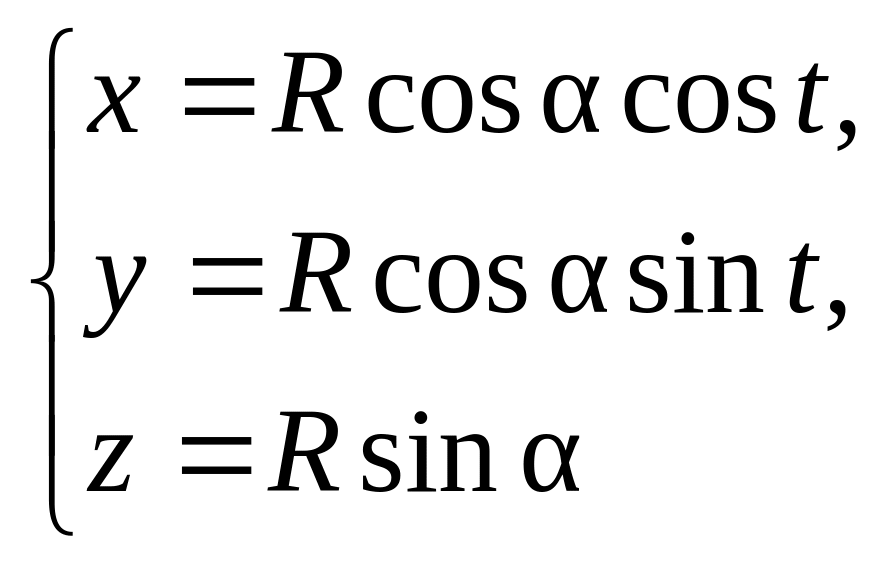8. Вычислить , если – отрезок прямой, соединяющий точки и .

9. Вычислить , где – дуга кубической параболы от точки до точке .

10. Вычислить , если – ломаная , где , , .

11. Вычислить , где – отрезок прямой от точки до точки .

12. Вычислить , где – отрезок прямой от точки до точки .

13. Вычислить , где – отрезок прямой, соединяющий точки и .