2. Криволинейный интеграл II рода

2.1. Основные понятия

Криволинейный интеграл II рода определяется почти так же, как и криволинейный интеграл I рода. Пусть в плоскости задана непрерывная кривая (или ) и непрерывная функция , определенная в каждой точке кривой. Разобьем кривую точками , , , …, , в направлении от точки к точке на «элементарных» дуг с длинами соответственно ( ). На каждой «элементарной» дуге выберем произвольно точку и составим сумму произведений вида (2.1), где – проекция дуги на ось (рис. 2.1). Сумму вида (2.1) называют интегральной суммой для функции по переменной . Таких сумм можно составить бесчисленное множество. Если при интегральные суммы вида (2.1) имеют конечный предел, не зависящий ни от способа разбиения кривой на части, ни от выбора точек , то его называют криволинейным интегралом II рода по координате от функции по кривой и обозначают (или ).

Таким образом, по определению, .

Аналогично вводится криволинейный интеграл II рода по координате от функции по кривой :

,

где – проекция дуги на ось .

Криволинейный интеграл II рода общего вида по кривой определяется равенством:

. (2.2)

Криволинейный интеграл II рода общего вида

(2.3)

по пространственной кривой определяется аналогично.

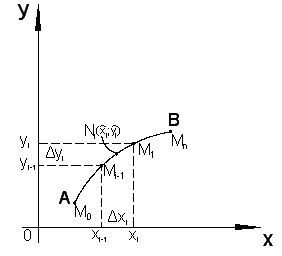
Рис.2.1

Теорема 2.1 (существование криволинейного интеграла II рода). Если кривая гладкая, а функции , (или в пространстве , , ) непрерывны по кривой , то криволинейный интеграл II рода существует.

2.2. Физический смысл криволинейного интеграла II рода

К интегралу вида (2.2) приводит решение физической задачи о вычислении работы переменной силы при перемещении материальной точки вдоль кривой на плоскости.

Разобьем кривую на части точками , , , …, , в направлении от точки к точке и рассмотрим ломанную, вершинами которой служат точки (рис. 2.2). Считая, что вдоль каждого звена ломанной линии сила сохраняет постоянное значение, равное , найдем ее работу на этом звене с помощью скалярного произведения вектора постоянной силы

на вектор прямолинейного перемещения

от точки до точки :

.

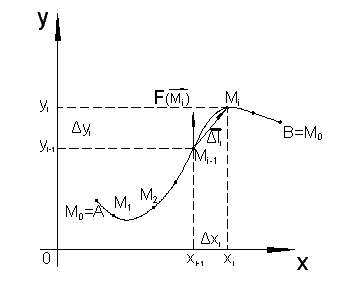
Рис. 2.2

Работу вдоль всей ломаной линии можно принять за приближенное значение работы , совершаемой переменной силой вдоль кривой :

. (2.4)

Предел суммы вида (2.4) при представляет собой криволинейный интеграл II рода общего вида в форме (2.2). Следовательно, искомая работа определяется по формуле:

. (2.5)

Замечание. Аналогичные рассуждения справедливы и для пространственной кривой , при этом формула (2.5) примет вид:

. (2.6)

Таким образом, криволинейный интеграл II рода от силы (или в пространстве ), под действием которой перемещается тело, определяет работу силы на пути . В этом состоит физический смысл криволинейного интеграла II рода.