Федеральное агентство по образованию

Волжский институт строительства и технологий

(филиал)

Волгоградского государственного архитектурно-строительного университета

Кафедра высшей математики

ПРЯМОЛИНЕЙНО

О КРИВОЛИНЕЙНЫХ ИНТЕГРАЛАХ

Методические указания для студентов

очной и заочной форм обучения

по дисциплине «Высшая математика»

Волжский 2008

УДК 517.3

Прямолинейно о криволинейных интегралах : метод. указ. для студентов очной и заочной форм обучения по дисц. «Высшая математика» / ВИСТех (филиал) ВолгГАСУ ; [Е. В. Абрамов, Е. Д. Илларионова]. – Волжский : ВИСТех (филиал) ВолгГАСУ, 2008. – 61 с.

Изложен основной теоретический материал, приведены примеры решения задач и задания для самостоятельной работы по каждому разделу. Включены задания для контрольной работы. Материалы могут быть использованы при самостоятельной подготовке по разделу «Криволинейные интегралы».

Данные методические указания предназначены для студентов 1-го курса очной и заочной форм обучения по дисциплине «Высшая математика».

Ил. 53 Библиогр. 7 назв.

1. Криволинейный интеграл I рода

1.1. Основные понятия

Обобщением определенного интеграла на случай, когда областью интегрирования выступает не отрезок, а некоторая кривая, является криволинейный интеграл.

Пусть на плоскости в декартовой прямоугольной системе координат задана непрерывная кривая (или ) длины , в точках которой определена некоторая непрерывная функция . Разобьем кривую точками , , , …, , на произвольных дуг с длинами соответственно ( ) (рис. 1.1). Выберем на каждой дуге произвольно точку и составим сумму произведений

, (1.1)

которая называется интегральной суммой для функции по кривой . Пусть – наибольшая из длин дуг деления. Если при (т. е. при ) существует конечный предел интегральных сумм вида (1.1), не зависящий ни от способа разбиения кривой на части, ни от выбора точек на них, то этот предел называют криволинейным интегралом I рода от функции по длине кривой (или ) и обозначают (или ), где – дифференциал дуги кривой .

Рис. 1.1

Таким образом, по определению:

. (1.2)

Аналогично определяется криволинейный интеграл I рода от функции трех переменных по пространственной кривой :

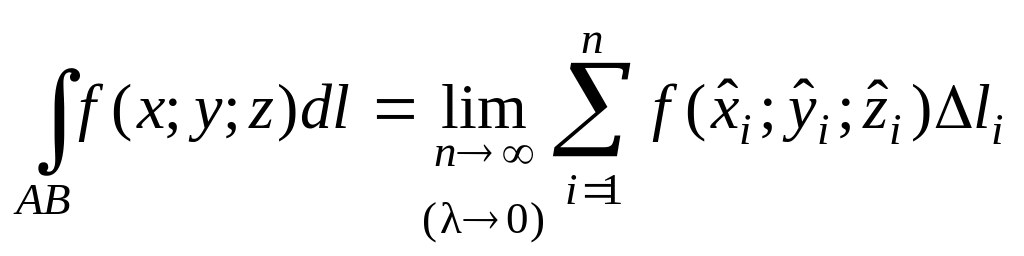. (1.3)

Если кривая интегрирования является замкнутой кривой, то криволинейный интеграл по этой кривой обозначается (или ).

Теорема 1.1. (существования криволинейного интеграла I рода). Если функция (или ) непрерывна в каждой точке гладкой¹ кривой, то криволинейный интеграл I рода вида (1.2) (или (1.3)) существует.

1.2. Геометрический и физический смысл криволинейного

интеграла I рода

Рассмотрим две задачи, приводящие к понятию криволинейного интеграла I рода по плоской кривой.

Площадь цилиндрической поверхности

Пусть в координатной плоскости задана гладкая кривая , на которой определена непрерывная функция . Тогда можно построить цилиндрическую поверхность: направляющей цилиндрической поверхности служит данная кривая , лежащая в плоскости , а образующая параллельна оси и цилиндрическая поверхность заключена между кривой и поверхностью (рис. 1.2). Площадь такой цилиндрической поверхности находится по формуле:

. (1.4)

В этом состоит геометрический смысл криволинейного интеграла I рода.

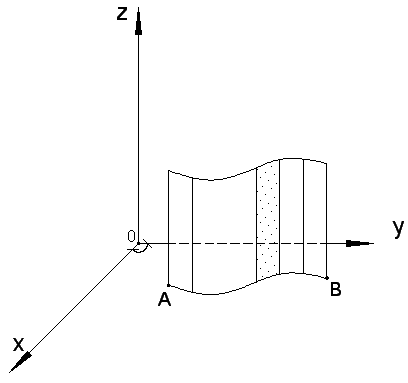
Рис. 1.2

Масса материальной кривой (цепь, провод, трос, канат и т. д.).

Пусть дана материальная кривая , имеющая в каждой точке плотность . Разобьем ее на элементарных дуг с длинами соответственно ( ). Пусть – произвольная точка дуги . Считая приближенно участок дуги однородным, т. е. плотность в каждой точке дуги такая же, как и в точке , найдем приближенное значение массы дуги : . Суммируя, находим приближенное значение массы всей кривой :

. (1.5)

Если кривая гладкая, а плотность задана непрерывной функцией в каждой точке кривой , то предел суммы (1.5) при условии, что (т. е. ) существует и его примем за массу кривой , т. е. , или, согласно формуле (1.2), получим:

. (1.6)

Таким образом, криволинейный интеграл I рода по кривой представляет собой массу материальной кривой , имеющей плотность , в чем и состоит механический смысл криволинейного интеграла I рода по кривой .

Замечание. Аналогичные рассуждения и формулы справедливы и для пространственной кривой интегрирования.