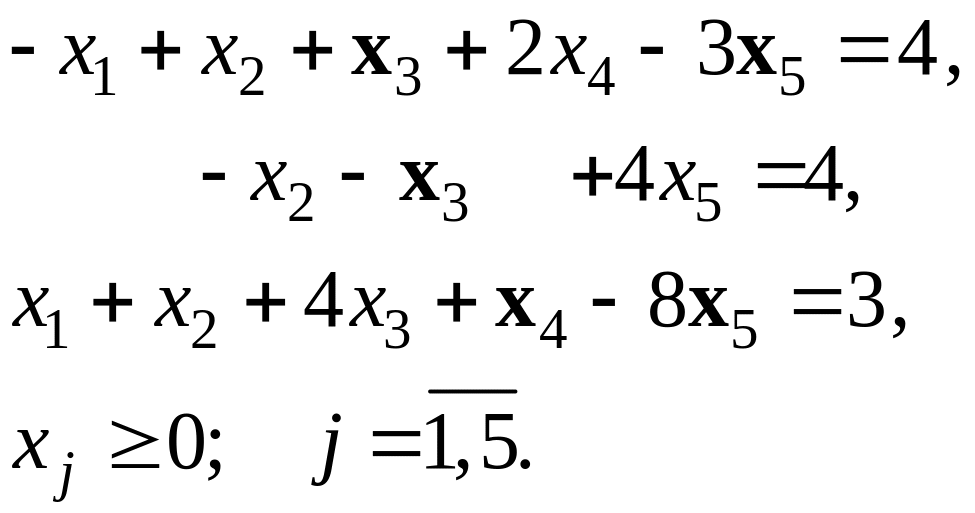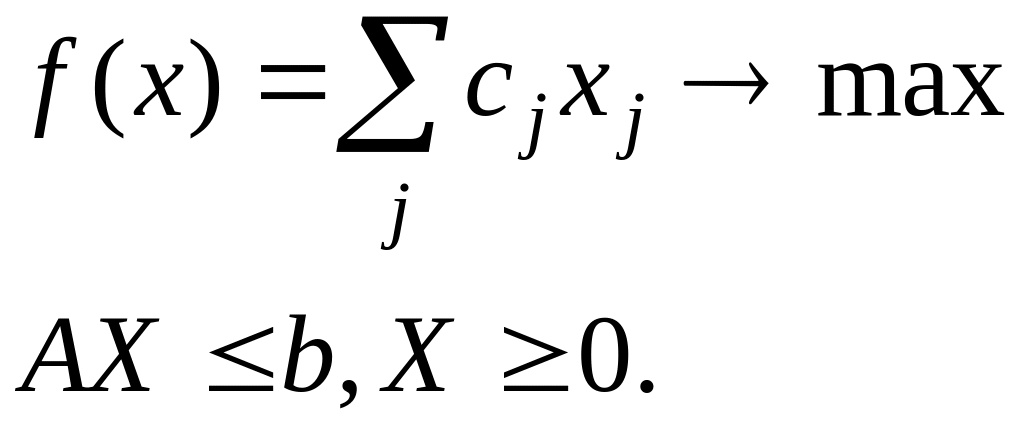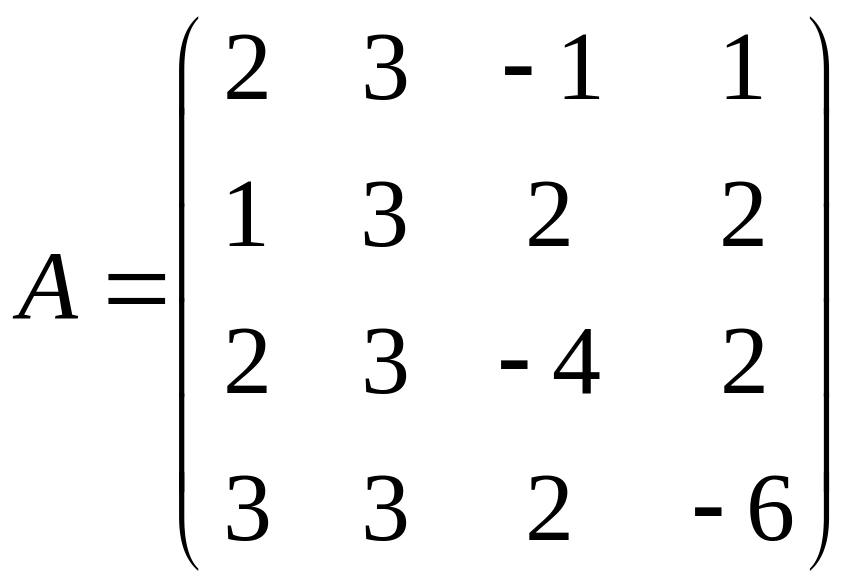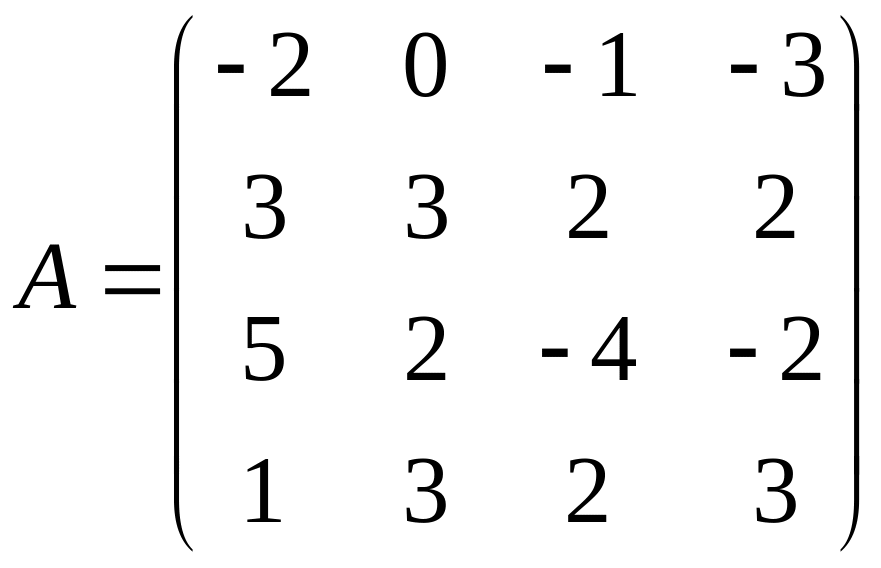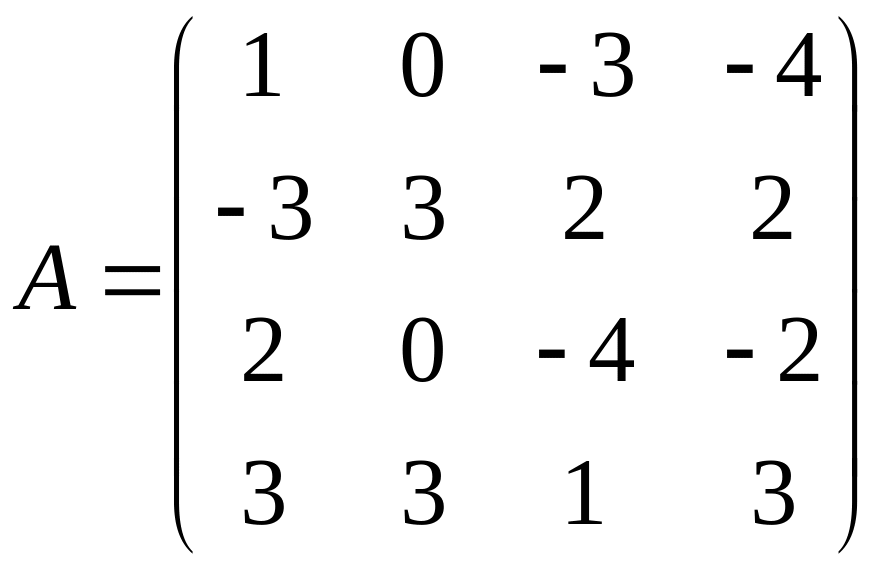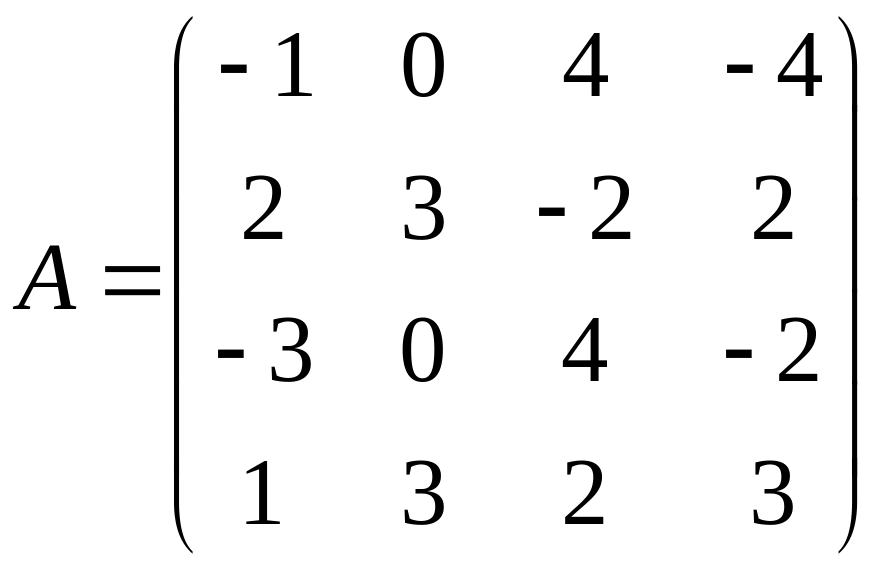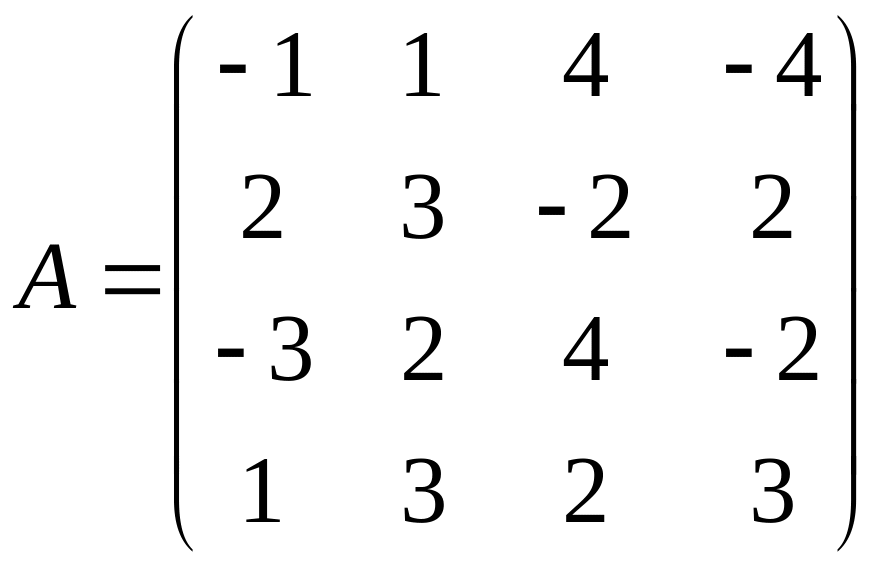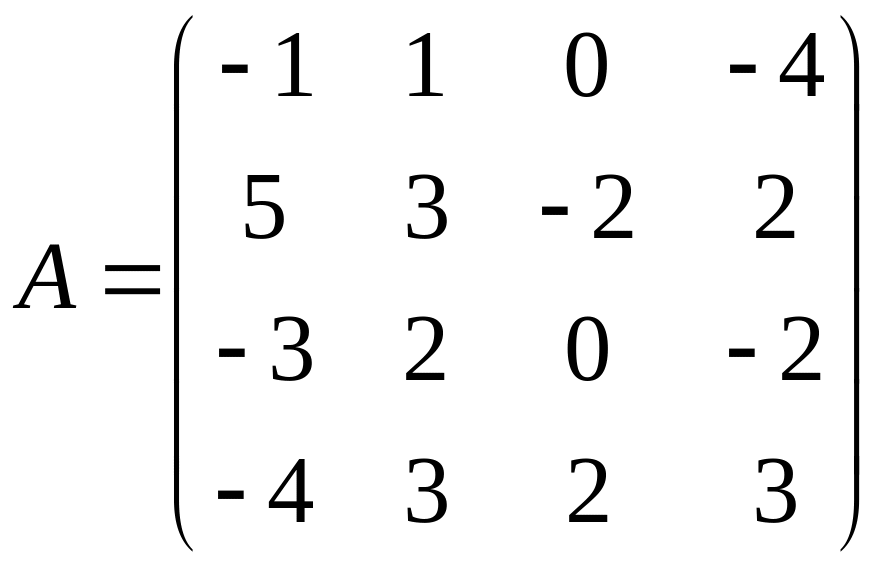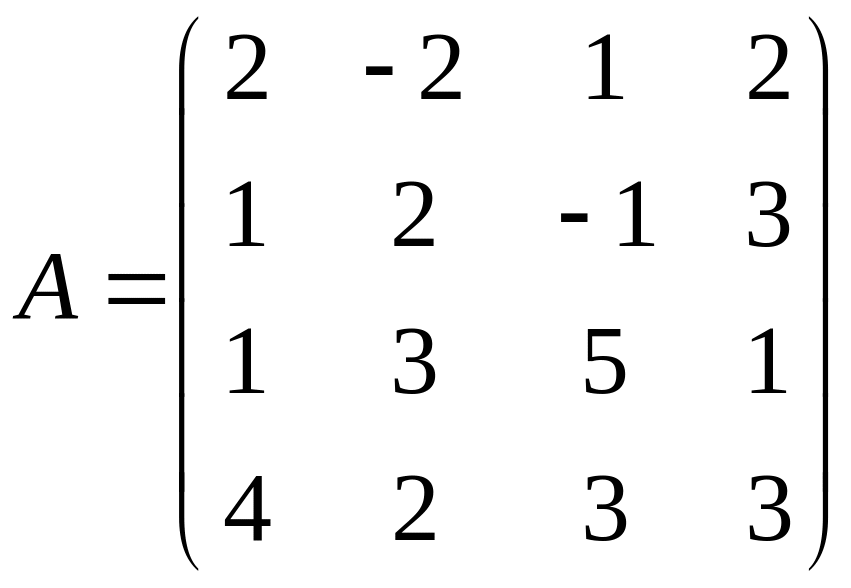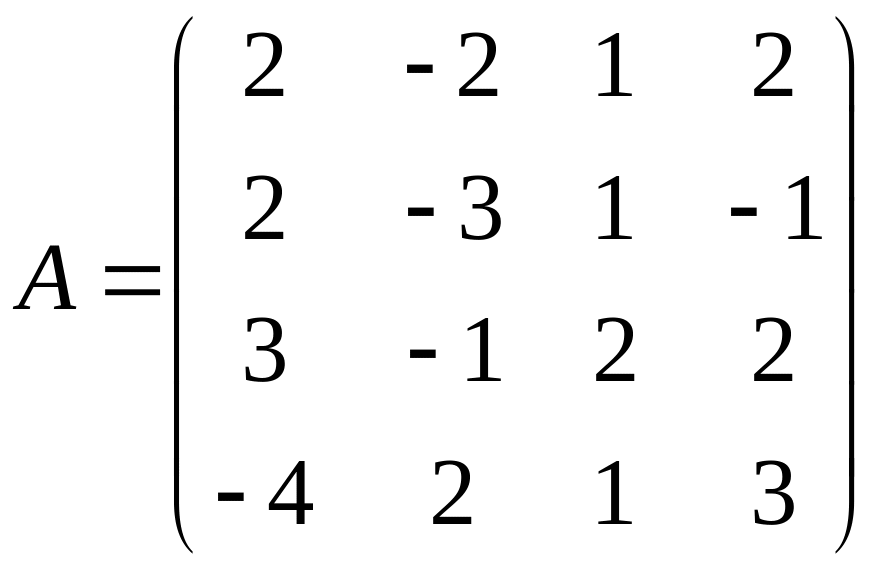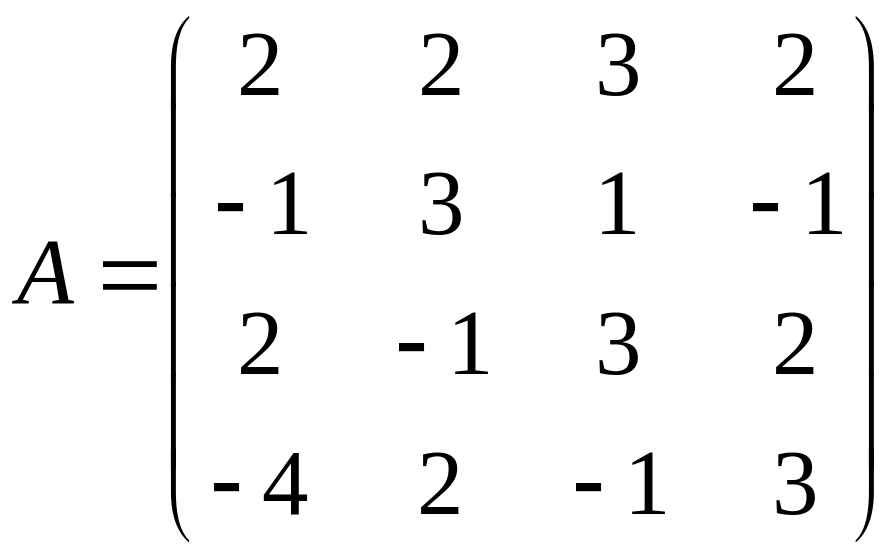Ситуации, в которых получение оптимального решения недостижимо

1) Предположим, что полученное БР задачи на максимум не оптимально: например, в индексной строке есть один положительный коэффициент. Тем самым определена переменная, которую, следует ввести в базис.

Вместе с тем коэффициенты базисного столбца неположительные. Следовательно, ввести эту переменную в базис нельзя: это приведет к недопустимому решению.

В таком случае задача не имеет решения по причине неограниченности ЦФ в ОДР.

2) Предположим, что при поиске первого базисного решения наталкиваемся на недопустимые решения и, не удаётся получить допустимого решения.

В таком случае задача не имеет решения по причине несовместности условий – ограничений задачи.

Пример решения задачи лп симплексным методом.

(1.6)

(1.7)

Решение.

Задача задана в канонической форме. Заполняем первый блок таблицы Гаусса и приступаем к поиску первого базисного допустимого решения.

					Св. чл.
-1	1	1	2	-3	4
0	-1	-1	0	4	4
1	1	4	1	-8	3	3:1
1	1	-1	-3	-7

					Св. чл.
0	2	5	3	-11	7
0	-1	-1	0	4	4	4:4
1	1	4	1	-8	3
0	0	-5	-4	1

					Св. чл.
0	-3/4	9/4	3	0	18	18:3
0	-1/4	-1/4	0	1	1
1	-1	2	1	0	11	11:1
0	1/4	-19/4	-4	0

					Св. чл.
0	-1/4	3/4	1	0	6
0	-1/4	-1/4	0	1	1
1	-3/4	5/4	0	0	5
0	-3/4	-7/4	0	0

Пояснения:

- первый разрешающий коэффициент взяли в первом столбце, т.к. он наиболее простой, в нем имеется один нуль;

- во второй таблице в качестве разрешающего взяли столбец с положительными коэффициентами индексной строки;

- в 3-й таблице в качестве разрешающего переменного можно взять или , хотя взять нужно , поскольку при коэффициент индексной строки положителен.

С другой стороны, взять нельзя, потому, что все коэффициенты этого столбца отрицательные – это приведёт к недопустимому решению. Поэтому в базис ввели .

Получено первое допустимое базисное решение.

Оно оптимально, т.к. в индексной строке нет положительных коэффициентов.

Замечание: При вычислении , отрицательные значения и нули не участвуют.