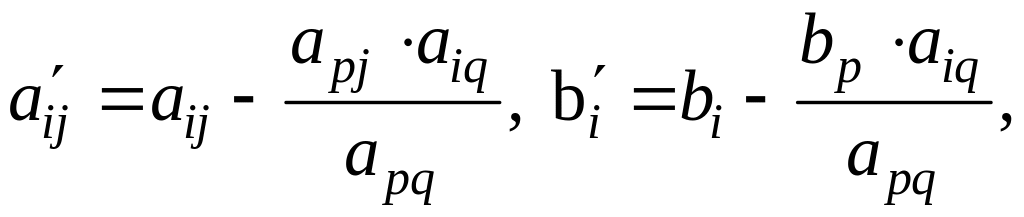Описание симплекс-метода

Все необходимые базисные решения удобно получать в таблице Гаусса.

Последнюю строку, которую назовём индексной строкой и заполняем её коэффициентами , свободный член

		…
		…
…	…	…	…	…
		…
		…

Каждая итерация осуществляется известными элементарными преобразованиями Гаусса:

Выбирается разрешающий (ведущий) коэффициент . разрешающий (ведущий) коэффициент нельзя брать в последней строке.

Разрешающая строка делится на , а разрешающий столбец заменяется единичным – с 1 вместо .

Все остальные элементы блока пересчитываются по формулам:

напоминающим мнемоническое правило прямоугольника (см. схему), или арифметическими действиями над строками таблицы при помощи разрешающей строки, если это возможно.

При этом надо следить за тем, чтобы новые свободные члены оставались неотрицательными.

Предположим, что ЗЛП (1.0) является невырожденной, а базисное решение (1.0) – допустимым.

Обозначим его:

тогда таблица имеет следующий вид

		…				…
		…	0	0		…
0	1	…	0	0		…
…	…	…	…	…	…	…	…	…
0	0	…	1	0		…
0	0	…	0	1		…
0	0	…	0	0		…

При этом .

В основе симплекс-метода (СМ) лежит следующая теорема.

Теорема оптимальности решения.

Допустимое базисное решение является оптимальным в том и только в том случае, когда среди коэффициентов индексной строки нет положительных в задаче на максимум (нет отрицательных в задаче на минимум).

Если коэффициенты индексной строки имеют разные знаки, то допустимое базисное решение не является оптимальным как в задаче на максимум, так и в задаче на минимум и следует переходить к другому базисному решению (плану).

Очередное допустимое базисное решение (план) получается тем же способом, но с учетом некоторых особенностей.

Рассмотрим задачу на максимум; задача на минимум решается по аналогичной схеме.

1) Разрешающий столбец надо выбирать так, чтобы не приобретать лишних положительных коэффициентов в индексной строке (хотя это иногда неизбежно, см. теорему оптимальности).

Иногда в качестве разрешающего берут столбец с максимальным коэффициентом индексной строки.

2) Неправильный выбор разрешающей строки может привести к недопустимому решению.

Правильный выбор строки сост. в следующем.

Предположим, что выбран разрешающий столбец с номером – .

Составим отношения

свободных членов уравнений к положительным коэффициентам разрешающего столбца (индексная строка здесь не участвует).

Найдём

.

Строку с этим числом надо считать разрешающей.

Если таких строк несколько, то выбор среди них безразличен.

3) Если ведущий (разрешающий) коэффициент выбран правильно, то соответствующие элементарные преобразования приводят только к допустимому решению.

При необходимости процедура нахождения допустимого базисного решения повторяется до получения оптимального решения, если оно существует.