Вариант 8

Завод получает 4 вида полуфабрикатов B_i в количествах: B₁– 400 т, B₂ – 250 т, B₃ –350 т и B₄ –100 т.

В результате смешения этих компонентов получают 3 вида продукции A_j. Пропорции смешиваемых полуфабрикатов следующие: для A₁– 2:3:5:2, для A₂ – 3:1:2:1, для A₃ – 2:2:1:3. Стоимость 1 т продукции A_j составляет: A₁ – 12 руб., A₂ –10 руб., A₃–15 руб.

Составить оптимальный план выпуска продукции по критерию максимальной стоимости выпущенной продукции.

Дополнительное задание:

1. Определить изменение максимальной стоимости продукции при изменении запасов полуфабрикатов : уменьшении запаса первого полуфабриката на 20 ед.; увеличении запаса второго полуфабриката на 40 ед.; увеличении запаса третьего полуфабриката на 30 ед.

Вариант 9

Завод получает 4 вида полуфабрикатов B_i в количествах: B₁– 450 т, B₂ – 200 т, B₃ –300 т и B₄ –150 т.

В результате смешения этих компонентов получают 3 вида продукции A_j. Пропорции смешиваемых полуфабрикатов следующие: для A₁– 2:4:5:3, для A₂ – 3:2:1:2, для A₃ – 1:2:4:3.

Составить оптимальный план выпуска продукции по критерию максимального использования полуфабрикатов.

Дополнительное задание:

1. Определить изменение максимального количества используемых полуфабрикатов при изменении запасов полуфабрикатов Bi: уменьшении запаса первого полуфабриката на 20 ед.; увеличении запаса второго полуфабриката на 40 ед.; увеличении запаса третьего полуфабриката на 30 ед.

Тема 2. Распределительные модели

При решении задач из этой темы необходимо ознакомиться с методами решения транспортной задачи [1, гл. 2, § 6 - §7, с. 85-110; 2, гл. 5, п. 5.1 – п. 5.5, с. 193-238].

Транспортная задача

2.1. Основные понятия

Пусть имеются m производителей и известны объемы запасов по каждому производителю: а₁, а₂, ..., а_m. Известна потребность в грузах b₁, b₂, ..., b_n каждого из n пунктов назначения. Задана матрица транспортных издержек от каждого производителя к каждому потребителю: . Необходимо рассчитать оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i– го пункта отправления в каждый j – й пункт назначения c минимальными транспортными издержками. Данные записываются в следующую таблицу:

Таблица 1. Общий вид транспортной таблицы.

	В1	В2	…	Вn	Запасы
А1	x11 c11	x12 c12	…	x1n c1n	а1
А2	x21 c21	x22 c22	…	x2n c2n	а2
…	…	…	…	…	…
Аm	xm1 cm1	xm2 cm2	…	xmn cmn	аm
Потребности	b1	b2	…	bn

Определение. Транспортная задача (ТЗ) называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения. Если такого равенства нет, то задачу называют открытой.

Суть этого определения в следующем: все потребности могут быть удовлетворены за счет запасов, и наоборот: все запасы разойдутся по потребителям без остатка. А значит, не требуются ни дополнительных поставщиков, ни дополнительных потребителей; не будет издержек, не будет дефицита.

Теорема 1. Для того чтобы ТЗ имела допустимые решения, необходимо и достаточно выполнения условия закрытости задачи.

Таким образом, если исходная ТЗ является открытой, необходимо преобразовать ее так, чтобы она стала закрытой. Правило преобразования будет описано далее в замечании.

Для написания модели необходимо записать следующие условия:

- все грузы из i- х пунктов должны быть отправлены:

.

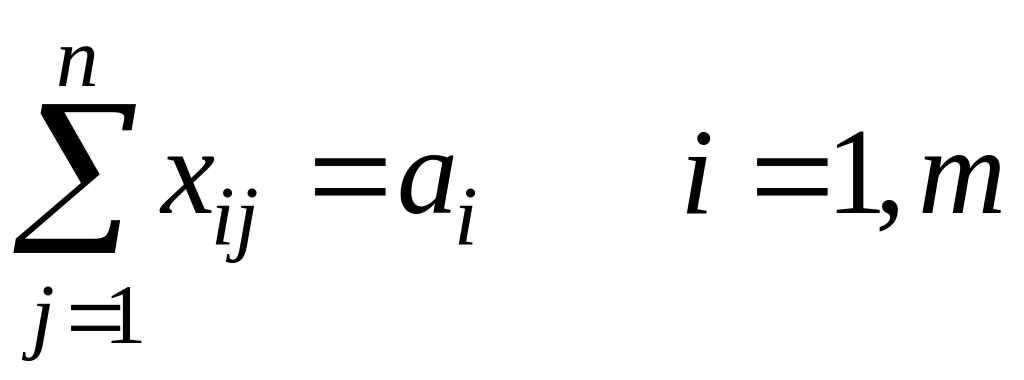- все j-е пункты потребления должны быть обеспечены грузами в полном объеме:

.

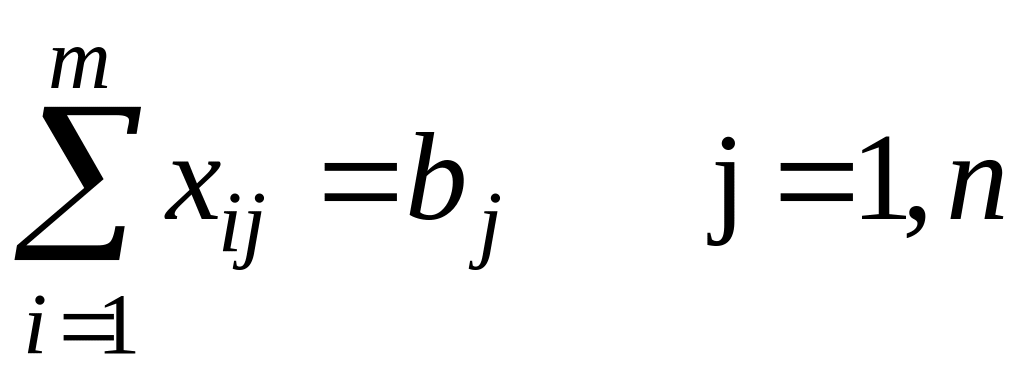Суммарные объемы отправления должны равняться суммарным объемам назначения:

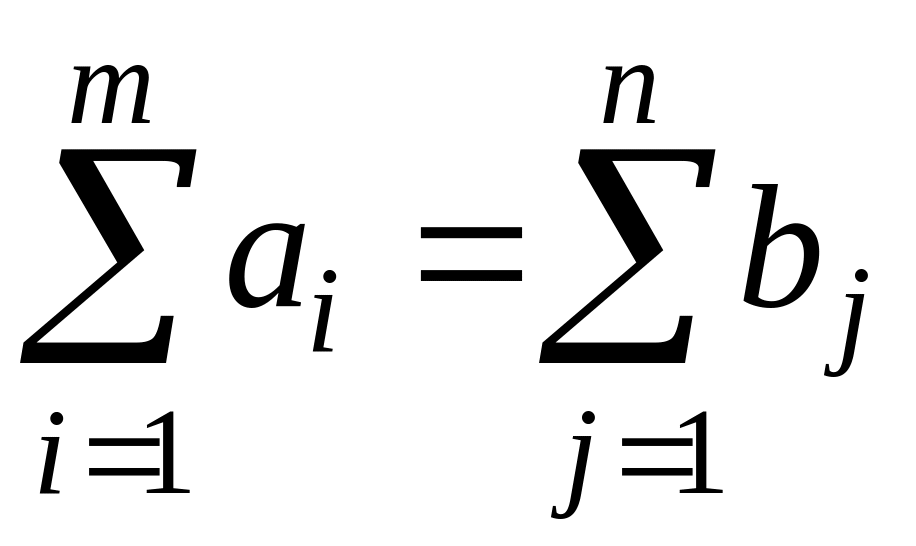
Должно выполняться условие неотрицательности переменных.

Перевозки необходимо осуществить с минимальными транспортными издержками:

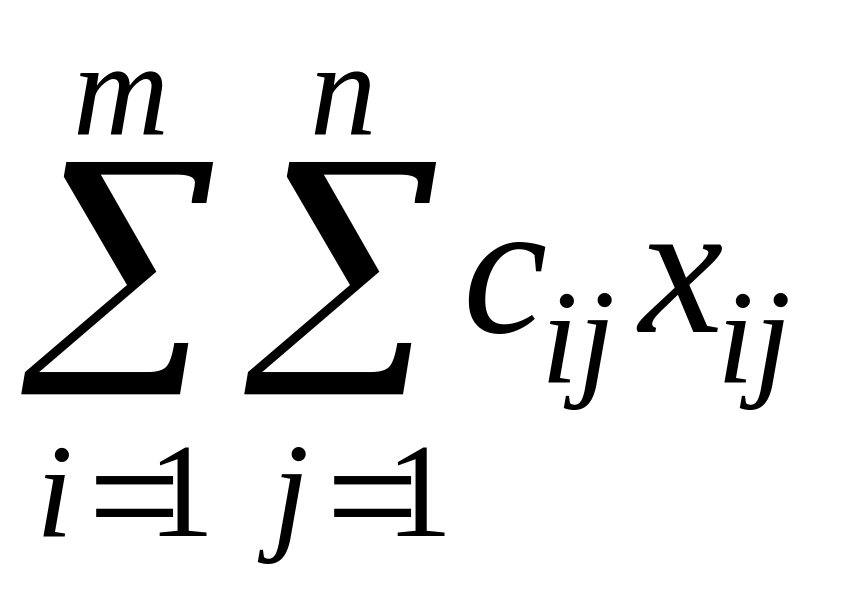
Z =  min.

Замечание.

Так как условие баланса суммарных поставок и потребностей является обязательным, то необходимо открытую задачу перевести в закрытую задачу по следующим правилам:

Если потребности превышают запасы, то вводится фиктивный поставщик с недостающим объемом отправления

Если запасы превышают потребности, то вводится фиктивный потребитель с недостающим объемом потребления.

Стоимость обслуживания транспортных потоков от фиктивных пунктов к реальным пунктам равна нулю.

Особенности транспортной задачи:

- распределению подлежат только однородные ресурсы,

- условия задачи описываются только уравнениями,

- все переменные выражаются в одинаковых единицах измерения,

- во всех уравнениях коэффициенты при неизвестных равны 1,

- каждая неизвестная встречается только в двух уравнениях системы ограничений.