2.4. Энтропия

Одной из функций состояния термодинамической системы является энтропия.

Энтропией называется величина, определяемая выражением

(2.13)

или для удельной энтропии

. (2.14)

Энтропия есть однозначная функция состояния тела, принимающая для каждого состояния вполне определенное значение.

Энтропия является экстенсивным (зависит от массы вещества) параметром состояния и в любом термодинамическом процессе полностью определяется начальным и конечным состоянием вещества и не зависит от пути протекания процесса.

Энтропию можно определить через основные параметры состояния термодинамической системы:

(2.15)

или для удельной энтропии

. (2.16)

В термодинамике обычно используется не абсолютное значение энтропии, а ее изменение в каком-либо термодинамическом процессе

(2.17)

поэтому энтропию часто отсчитывают от произвольно выбранного уровня.

Для вычисления энтропии идеального газа в различных термодинамических процессах используют следующие уравнения

(2.18)

…… (2.19)

(2.20)

Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов ─ диаграмму, на которой состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией (рисунок 2.2).

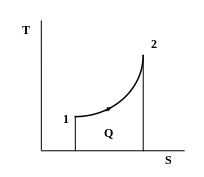
Рисунок 2.2 ─ Графическое изображение количества теплоты в виде

площади под кривой процесса в -диаграмме

По характеру изменения энтропии в равновесном процессе можно судить о том, в каком направлении происходит теплообмен.

Если энтропия системы возрастает , то к системе подводится тепло.

Если , то , т. е. от системы отводится тепло.

Если энтропия системы не изменяется , то отсутствует теплообмен с окружающей средой, т.е. процесс адиабатный.

2.5 Энтальпия

Одним из важнейших параметров в термодинамике является энтальпия.

Введение этого параметра упрощает рассмотрение процессов в тепловых двигателях, особенно при исследовании процессов, в которых рабочим телом является водяной пар.

Под энтальпией понимают энергию расширенной системы, состоящей из макротела (газа) и поршня с грузом, уравновешивающего давление газа внутри сосуда, куда заключен газ.

Энтальпия равна сумме внутренней энергии системы и потенциальной энергии поршня с грузом

(2.21)

Физический смысл энтальпии поясним на следующем примере.

Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом общим весом (рисунок 2.3).

Рисунок 3.

Энергия этой системы складывается из внутренней энергии газа и потенциальной энергии поршня с грузом:

В условиях равновесия эту систему можно выразить через параметры состояния газа

Получаем, что , т.е. энтальпию можно трактовать как энергию расширенной системы.

Так как входящие в уравнение (2.21) величины являются функциями состояния, то и сама энтальпия является функцией состояния.

Также как внутренняя энергия, работа и теплота энтальпия измеряется в джоулях.

.

Удельная энтальпия представляет собой энтальпию системы, содержащей 1 кг вещества

. (2.22)

Энтальпия может быть представлена в виде функции двух любых параметров состояния

. (2.23)

Так как между энтальпией и внутренней энергией существует связь , то выбор начала отсчета одной из них не произволен: в точке, принятой за начало отсчета внутренней энергии .

Например, для воды при и , , а .