Лекция 7. Исследование функций

1. Возрастание и убывание функций

Промежутки, в которых функция возрастает или убывает, называются промежутками монотонности.

Установим необходимые и достаточные условия монотонности функции.

Теорема 1 (необходимые условия монотонности). Если дифференцируемая на интервале (a, b) (т.е. имеет производную в каждой точке этого интервала) функция f(x) возрастает (убывает), то производная функции во всех точках этого интервала неотрицательна (неположительна), т.е. f'(x) ≥ 0 (f'(x) ≤ 0) для любого .

Доказательство. Пусть f(x) возрастает на интервале (a, b). Возьмем произвольные точки х и х + Δх на интервале (a, b) и рассмотрим отношение .

Функция f(x) возрастает, поэтому

если Δх > 0, то х + Δх > x и f(х + Δх) > f(x);

если Δх < 0, то х + Δх < x и f(х + Δх) < f(x).

В обоих случаях , так как числитель и знаменатель имеют одинаковые знаки.

По условию теоремы f(x) имеет производную в точке х и является пределом рассматриваемого отношения. Следовательно,

. Теорема доказана.

Аналогично доказывается случай, когда f(x) убывает на интервале.

Геометрический смысл необходимого условия возрастания функции: касательные к графику возрастающей дифференцируемой функции образуют острые углы с положительным направлением оси Ох или в некоторых точках параллельны оси Ох (на рис. 1 в точке х₀).

Рис. 1

Замечание. Сформулированное условие является необходимым, но не достаточным.

Например, на участках монотонности функции могут встречаться точки, в которых функция вообще не имеет производной.

Пример. График возрастающей на всей числовой оси функции у = 2x + |х| в точке х = 0 имеет излом (рис. 2), т.е. производная в этой точке f'(х = 0) не существует.

Рис. 2

Теорема 2 (достаточные условия монотонности). Если функция f(x) дифференцируема на интервале (a, b) и во всех его точках имеет положительную (отрицательную) производную (т.е. f'(x) > 0 (f'(x) < 0)), то функция строго возрастает (строго убывает) на этом интервале (a, b).

Доказательство. Пусть х₁ и х₂ – две произвольные точки интервала (a, b), причем х₁ < х₂. Применим к отрезку [х₁, х₂] теорему Лагранжа, т.е. существует точка с є (х₁; х₂) такая, что f(х₂) – f(х₁) = f'(с) (х₂ – х₁).

Если f'(x) > 0, то для х₁ < х₂ из формулы Лагранжа (при f'(с) > 0 и (х₂–х₁)>0) следует, что f(х₂) – f(х₁) > 0 или f(х₂) > f(х₁). Последнее неравенство означает, что f(x) на интервале (a, b) строго возрастает.

Если f'(x) < 0 (т.е. f'(с) < 0), то для (х₂ – х₁) > 0 находим, что f(х₂) – f(х₁) < 0 или f(х₂) < f(х₁), т.е. f(x) на интервале (a, b) строго убывает. Теорема доказана.

Замечание. Сформулированное в теореме 2 условие у' > 0 является достаточным для строгого возрастания функции, но не является необходимым.

Например, функция у = х³ строго возрастает на всей числовой оси (рис. 3). Вместе с тем, ее производная у' = 3х² обращается в нуль при x = 0. То есть производная функции х³ на всей числовой оси является неотрицательной у' ≥ 0.

Рис. 3

Теоремы 1 и 2 позволяют исследовать функцию на монотонность.

Рассмотрим графики функций y=f(x), у=g(x) и у=(х) на рис. 4, 5, 6.

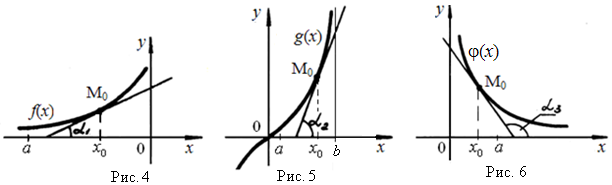
На рис. 4 и 5 функции f(х) и g(x) возрастают, но график на рис. 4 – пологий на участке [а, 0], т.е. функция f(x) растет медленно. График g(x) на рис. 5 круто поднимается вверх на участке [а, b], т.е. растет с большей скоростью. Сравним углы наклона касательных ₁ и ₂ к графикам в точке М₀, которые они образуют с положительным направлением Ох. Так как углы ₁ и ₂ – острые, то tg₁>0 и tg₂ > 0, т.е. производные положительны. Поскольку tg₁ < tg₂ (т.е. f'(х) < g'(x)), то график g(x) растет «круче», чем график f(x).

На рис. 6 график функции (х) убывает на [х₀, а]. Угол касательной с осью Оx ₃ – тупой, и tg₃ = '(х₀) < 0.

Пример. Исследовать f(x) = x² + 2x – 3 на возрастание и убывание.

Решение. Область определения функции: R = (-∞, ∞).

Производная f'(x) = 2(x + 1) = 0. Откуда x = -1. Этой точкой разобьем область определения на два интервала: (-∞; -1) и (-1; ∞).

При x є (-∞; -1) f'(x) < 0, т.е. f(x) убывает на интервале (-∞; -1);

при x є (-1; ∞) f'(x) > 0, т.е. f(x) возрастает на интервале (-1; ∞).