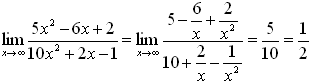5. Связь между бесконечно большой и бесконечно малой функциями

Величина, обратная бесконечно большой величине при ха, есть бесконечно малая, и наоборот, т.е. при ха (х∞)

и .

Данную связь символически запишем как и .

Пример 1. => – есть бесконечно малая при х∞, так как по мере неограниченного возрастания х абсолютное значение величины стремится к нулю.

Пример 2. => – бесконечно большая при х0, так как по мере приближения значений х к нулю абсолютное значение величины неограниченно возрастает.

Пример 3. Функция y = cos x при х - бесконечно малая: , а функция при х - бесконечно большая:

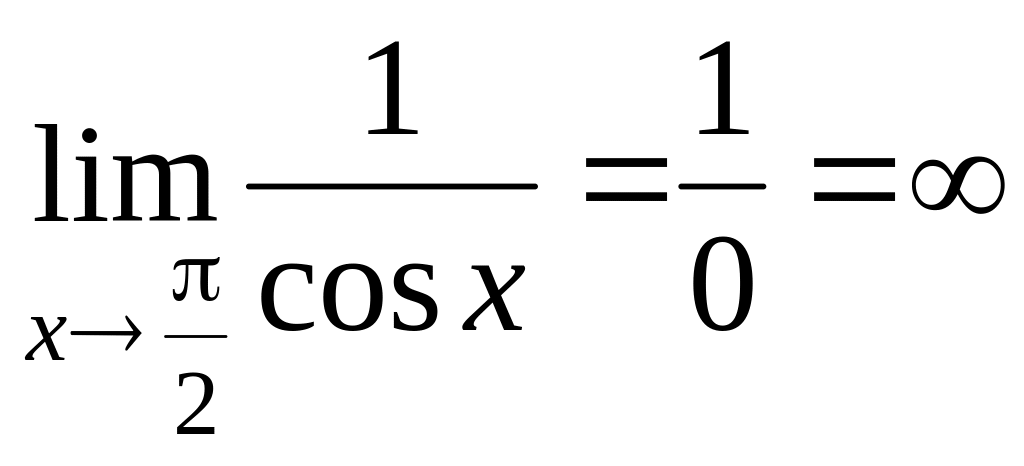
6. Основные свойства пределов (теоремы о пределах)

1. Функция не может иметь более одного предела.

Докажем это свойство. Предположим противное, т.е. что функция f(x) имеет два разных предела b и с:

, , b ≠ c.

Поскольку утверждения «число b есть предел величины у» и «разность у – b есть бесконечно малая величина» равнозначны, то величины

α(x) = f(x) – b, β(x) = f(x) – c

бесконечно малы при х → а. Вычитая почленно эти равенства, получим

α(x) – β(x) = с – b ≠ 0,

что невозможно, поскольку переходя в этом равенстве к пределу при х → а, имеем: . Следовательно, предположение о существовании второго предела неверно.

2. Предел постоянной величины y = с есть само число с: lim с = с.

Пусть y, …, z, u, v – функции, для которых существуют пределы в точке а (не исключаем случая а = ∞).

3. Предел алгебраической суммы (т.е. сумма или разность) конечного числа функций y, u, ..., z равен такой же сумме пределов этих функций:

lim(y ± u ±....± z) = limy ± limu ±....± limz;

4. Предел произведения конечного числа функций y, u, ..., z равен произведению пределов этих функций:

lim(y · u ·...· z) = limy · limu ·...· limz.

В частности, постоянный множитель можно выносить за знак предела, т. е.

5. Предел частного равен частному пределов:

.

Если предел делителя равен нулю (lim = 0), а limu = с ≠ 0, то запись следует понимать в том смысле, что . Таким образом, будем считать, что .

Аналогичные записи можно применять и для односторонних пределов:

Пример 1. .

Если limu=0 и lim=0, теорема неприменима, так как выражение является неопределенным. Но теорема остается верной. «Сокращать» на нуль и писать 1 вместо нельзя. Этот символ закрывает прямой путь подстановки и заставляет искать путь раскрытия этой неопределенности (например, с помощью сокращения общих множителей).

6. Пусть y=f(u), u=φ(x). Тогда y=f(φ(x)) – сложная функция.

Если , , то предел сложной функции

.

7. Если limf(x) = b > 0, limg(x) = c, то имеет место соотношение

lim(f(x))^g(x) = (lim(f(x))^limg(x) = b^c.

8. Если в некоторой окрестности точки а (окрестностью точки ∞ считаем множество достаточно больших х) выполняется нестрогое неравенство f(x)≤g(x), то для соответствующих пределов выполнено нестрогое неравенство:

.

(Заметим, что если в окрестности точки а выполняется строгое неравенство f(x)<g(x), то утверждение теоремы сохраняет свою силу, так как из строгого неравенства в пределе получается, вообще говоря, нестрогое).

9. Если в некоторой окрестности точки а функция f(x) заключена между двумя функциями и(х) и v(x), имеющими одинаковый предел b при х → а, то функция f(x) имеет тот же предел b:

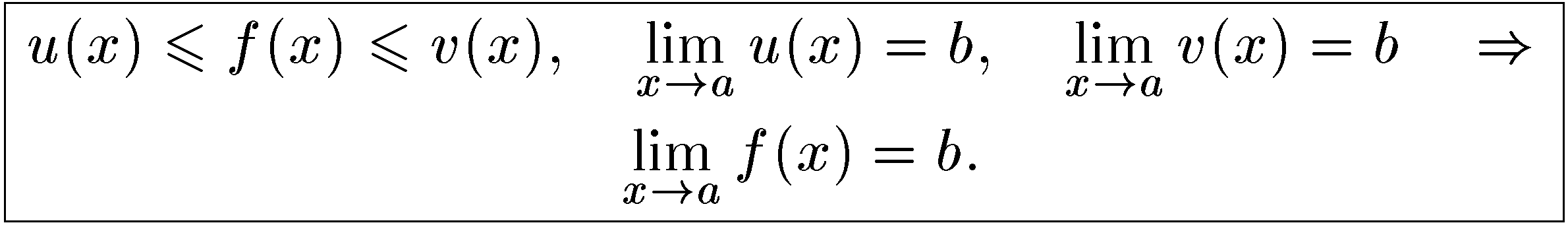
Свойства пределов облегчают их вычисление.

Пример 2. Найти предел функции при x1.

Решение. Воспользуемся свойствами пределов и найдем отдельно пределы числителя и знаменателя:

=7∙1-4∙1+2=5,

Применяя свойство 3, получим предел дроби: .

Непосредственное применение свойств пределов сразу привело к получению ответа.

На практике такие случаи встречаются крайне редко, а потому, прежде чем применять теоремы о пределах, приходится тождественно преобразовывать данную функцию.

Пример 3. Найти предел функции при x.

При этом и числитель, и знаменатель также стремятся к бесконечности. Символически этот случай обозначают [/] и называют «неопределенностью типа [/]». Очевидно, что непосредственно применить теорему о пределе частного здесь нельзя. Для раскрытия неопределенности преобразуем предварительно данную дробь, разделив и числитель, и знаменатель на х³ (старшую степень знаменателя):

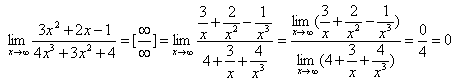
Величины – бесконечно малые при x, и их пределы равны нулю. Итак, предел функции у равен нулю, следовательно, при x у – бесконечно малая функция.

Пример 4. Найти .

Решение. Вновь получили неопределенность типа [/].

Применим только что использованный прием, и числитель, и знаменатель поделим на х⁵ (старшую степень числителя):

.

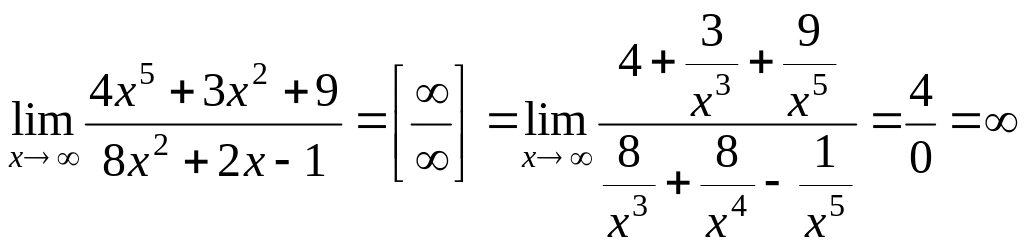Предел числителя в полученной дроби равен 4, а предел знаменателя равен нулю, знаменатель при x - бесконечно малая величина. Вся дробь является величиной, обратной бесконечно малой, т.е. бесконечно большой, и ее предел равен бесконечности.

Пример 5. Найти . Решение: