
- •Раздел 1. Дифференциальное исчисление Лекции 2 и 3. Предел функции
- •Понятие предела функции
- •Предел функции в бесконечности
- •Бесконечно малые величины
- •Свойства бесконечно малых величин
- •Бесконечно большие величины
- •Свойства бесконечно больших величин
- •Связь между бесконечно большой и бесконечно малой функциями
- •Основные свойства пределов (теоремы о пределах)
- •Виды неопределенностей
- •Первый и второй замечательные пределы
- •Сравнение бесконечно малых
- •Принцип замены эквивалентных
- •Свойства символа «о»-малое
Бесконечно малые величины
Определение.
Функция называется (х)
называется бесконечно
малой величиной
в какой-то точке a,
если она имеет нулевой предел в этой
точке:
![]() .
.
Пример 1.
α(x)
= 4x
– 20 – бесконечно малая величина в точке
х
= 5, так как при х5
будет
![]() .
.
Пример 2.
β(x)
= ln(3x
– 8) – бесконечно малая величина в точке
х
= 3, так как при х3
будет
![]() .
.
Зная определение предела функции при ха и при х∞, дадим развернутое определение бесконечно малой величины с помощью кванторов:
при ха:
![]() ,
,
при х∞:
![]() .
.
Существует связь бесконечно малой величины с функцией, имеющей конечный предел: функция f(x) в какой-то точке а имеет конечный предел b тогда и только тогда, если она вблизи этой точки а отличается от числа b на бесконечно малую функцию, т.е.
f(x) = b + α(x), где .
Пример 3.
α(x)=4x–20
– бесконечно малая величина в точке х
= 5, а функция f(x)=х2+3
в этой же точке х=5
имеет конечный предел:
![]() .
.
Тогда при х5 будет f(x)=b+α(x) х2+3=28+4x–20=8+4x.
Свойства бесконечно малых величин
Сумма бесконечно малых величин бесконечно мала: α(x) = α1(x) + α2(x).
Пример 3. α(x) = 4x – 20 и β(x) = ln(3x – 14) – бесконечно малые величины в точке х=5.
Тогда при х5
будет
![]() .
.
Произведение бесконечно малой величины на ограниченную функцию (в том числе на постоянную или на другую бесконечно малую) бесконечно мало:
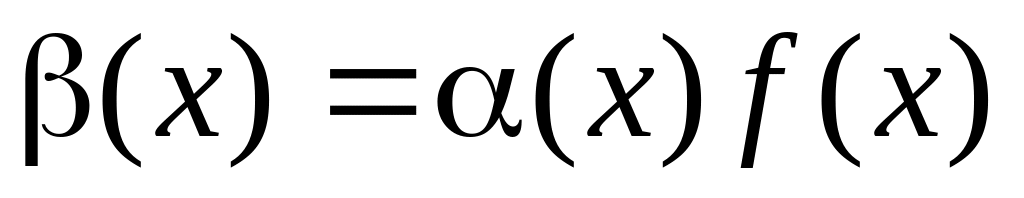 ,
где
,
где
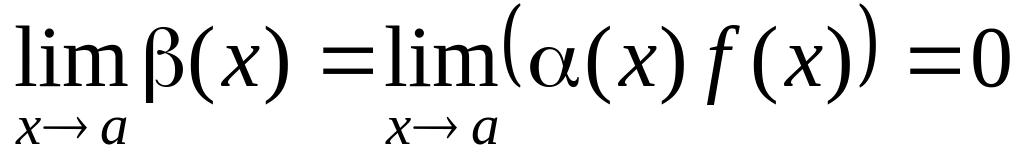 .
Здесь f(x)
– ограниченная.
.
Здесь f(x)
– ограниченная.
Функция f(x) называется ограниченной на заданном множестве значений ее аргумента X, если можно подобрать такую ограничивающую константу m>0, что при всех значениях хєX выполняется |f(x)|≤m.
Пример 4.
α(x)
= 4x
– 20 – бесконечно малая величина в точке
х=5,
а f(x)=(3x
– 14) ограничена в окрестности этой точки
хє(4;
6) числом m=4
(так как 3·6-14=4). Тогда в точке х=5
произведение α(x)·f(x)
– бесконечно малая величина, т.е.
![]() .
.
Частное от деления бесконечно малой величины на функцию, имеющую ненулевой предел, - бесконечно мало:
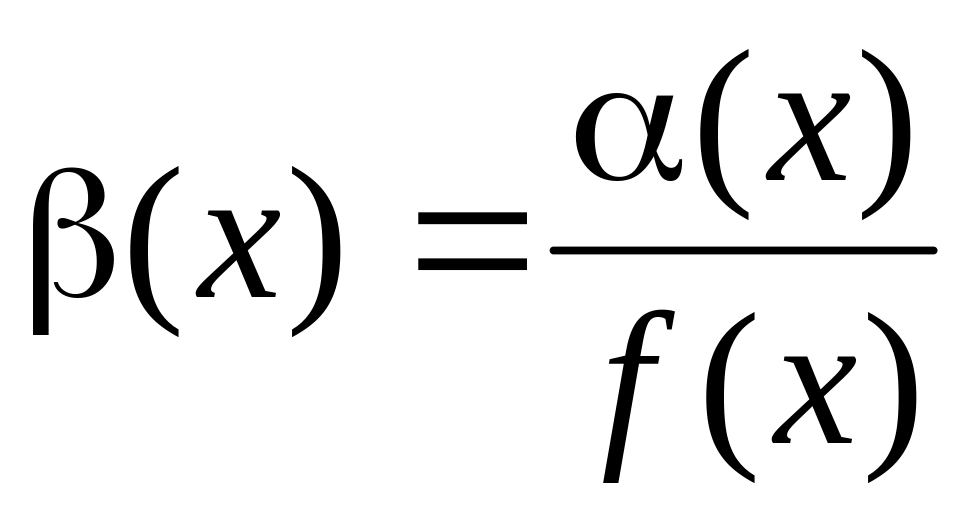 ,
,
т.е.
![]() ,
где
,
где
![]() .
.
Бесконечно большие величины
Определение. Функция f(x) называется бесконечно большой величиной в какой-то точке a прикосновения множества допустимых значений х, если для любого сколь угодно большого числа М>0 можно указать такую окрестность в точке a, в которой при всех допустимых x выполняется неравенство |f(x)|>M.
Иногда говорят, что бесконечно большой величиной называется переменная величина, абсолютное значение которой неограниченно возрастает. Однако неограниченная функция не обязательно бесконечно большая. Например, функция х sinх – неограниченная (ее значения могут быть как угодно большими), но не является бесконечно большой при х∞, так как с ростом х функция все время колеблется.
Предел бесконечно
большой величины равен бесконечности:
![]() .
.
Зная определение предела функции при ха и при х∞, дадим развернутое определение бесконечно большой величины с помощью кванторов:
при ха:
![]() ,
,
при х∞:
![]() .
.
Пример.
Функция у
= tg x
есть бесконечно большая величина при
![]() :
:
![]() .
.
Свойства бесконечно больших величин
Произведение бесконечно большой величины на функцию, имеющую ненулевой предел, - бесконечно большая величина.
Сумма бесконечно большой величины и ограниченной функции - бесконечно большая.
Частное от деления бесконечно большой величины на функцию, имеющую ненулевой предел, - бесконечно большая величина.
