
- •Раздел 3 Множество действительных чисел и его подмножества
- •§1 Операции и отношения на множестве действительных чисел.
- •III Связь операций сложения и умножения.
- •§2 Основные подмножества множества действительных чисел.
- •§3 Ограниченные и неограниченные множества и их свойства.
- •§4 Принцип Архимеда.
- •§5 Теорема Кантора (принцип вложенных отрезков).
Раздел 3 Множество действительных чисел и его подмножества
§1 Операции и отношения на множестве действительных чисел.
I
Операция сложения.
Для
любых двух действительных чисел
 и
и
 определено единственное число, называемое
их суммой и обозначаемое
определено единственное число, называемое
их суммой и обозначаемое
 ,
причем:
,
причем:

 коммутативность
сложения;
коммутативность
сложения;

 ассоциативность
сложения;
ассоциативность
сложения;

 существование
нуля (далее обозначаем
существование
нуля (далее обозначаем ;
;
 существование
противоположного числа (далее обозначаем
существование
противоположного числа (далее обозначаем .
.
Число
 называется разностью чисел
и
и обозначается
называется разностью чисел
и
и обозначается
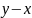 .
Свойства
.
Свойства
 называются аксиомами сложения. Из аксиом
сложения немедленно следует единственность
нуля и противоположного числа. (Доказать
самостоятельно!).
называются аксиомами сложения. Из аксиом
сложения немедленно следует единственность
нуля и противоположного числа. (Доказать
самостоятельно!).
II
Операция умножения.
Для
любых двух действительных чисел
и
определено единственное число, называемое
их произведением и обозначаемое
 ,
причем:
,
причем:
 коммутативность
умножения;
коммутативность
умножения;
 ассоциативность
умножения;
ассоциативность
умножения;
 существование
единицы (далее обозначаем
существование
единицы (далее обозначаем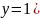 ;
;
 существование
обратного числа (далее обозначаем
существование
обратного числа (далее обозначаем .
.
Число
 (
(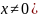 называется
частным от деления чисел
и
и обозначается
называется
частным от деления чисел
и
и обозначается
 .
Свойства
.
Свойства
 называются аксиомами умножения. Из
аксиом умножения немедленно следует
единственность единицы и обратного
числа. (Доказать самостоятельно!).
называются аксиомами умножения. Из
аксиом умножения немедленно следует
единственность единицы и обратного
числа. (Доказать самостоятельно!).
III Связь операций сложения и умножения.
 аксиома
дистрибутивности.
аксиома
дистрибутивности.
IV
Отношение порядка.
Для любых двух различных действительных
чисел
и
имеет место одно из двух соотношений:
либо
 ,
или что то же самое
,
или что то же самое
 ,
либо
,
либо
 ,
или, что то же самое
,
или, что то же самое
 .
Причем выполнены следующие условия:
.
Причем выполнены следующие условия:

 аксиома
транзитивности;
аксиома
транзитивности;

 ;
;

 .
.
Отношения
порядка называют сравнением действительных
чисел по величине или неравенствами.
Неравенство
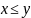 равносильное записи
равносильное записи
 означает, что либо
,
либо
означает, что либо
,
либо
 .
.
Из аксиом порядка следует свойство множества действительных чисел, называемое плотностью:
 .
.
Действительно,
из аксиомы
следует, что
 и
и
 .
Тогда из аксиомы
следует, что
.
Тогда из аксиомы
следует, что
 и
и
 ,
т.е. в качестве искомого
,
т.е. в качестве искомого
 можно взять
можно взять
 .
.
V
Непрерывность.
Для
любых двух непустых множеств
 и
и
 ,
таких, что:
,
таких, что:
 ,
найдется число
,
найдется число
 ,
так, что
,
так, что
 .
.
Свойства I-V полностью определяют множество действительных чисел, поэтому дадим аксиоматическое определение этого множества:
Определение Множество элементов, обладающее свойствами I-V и содержащее более одного элемента, называется множеством действительных чисел, а каждый его элемент – действительным числом.
Это определение однозначно задает множество действительных чисел с точностью до природы его элементов. Требование о том, чтобы в множестве было более одного элемента необходимо, т.к. множество, состоящее из одного нуля очевидно удовлетворяет свойствам I-V.
§2 Основные подмножества множества действительных чисел.
Числа
 ,
,
 ,
,
 ,
… и т.д. называются натуральными числами
и их множество обозначается
,
… и т.д. называются натуральными числами
и их множество обозначается
 .
Таким образом, множество натуральных
чисел обладает свойством индуктивности,
которое заключается в следующем:
.
Таким образом, множество натуральных
чисел обладает свойством индуктивности,
которое заключается в следующем:
1)
 ;
;
2)
 .
.
Причем
оно является наименьшим множеством,
обладающим таким свойством, т.е. если
 и
и
 обладает свойством индуктивности, то
обладает свойством индуктивности, то
 .
На этом свойстве множества натуральных
чисел основан принцип доказательства
методом математической индукции.
.
На этом свойстве множества натуральных
чисел основан принцип доказательства
методом математической индукции.
Числа
 называются целыми, их множество
обозначается
называются целыми, их множество
обозначается
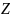 .
Множество целых чисел счетно, их можно
занумеровать. располагая в цепочку
следующим образом:
.
Множество целых чисел счетно, их можно
занумеровать. располагая в цепочку
следующим образом:
 .
.
Числа
вида
 ,
где
,
где
 ,
а
,
а
 ,
причем
,
причем
 ,
называются рациональными. Множество
всех рациональных чисел обозначают
,
называются рациональными. Множество
всех рациональных чисел обозначают
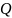 .
Таким образом,
.
Таким образом,
 ,
,
,
,
,
,
 .
Множество рациональных чисел счетно
(доказать самостоятельно!). Действительные
числа, не являющиеся рациональными,
называются иррациональными и их множество
обозначается
’.
.
Множество рациональных чисел счетно
(доказать самостоятельно!). Действительные
числа, не являющиеся рациональными,
называются иррациональными и их множество
обозначается
’.
Геометрически
множество действительных чисел
изображается направленной прямой, а
отдельные числа – точками этой прямой.
Поэтому совокупность действительных
чисел еще называют числовой прямой или
числовой осью. Таким образом, неравенство
означает, что точка
лежит левее точки
на числовой оси. Дополним множество
действительных чисел элементами
 (минус бесконечность) и
(минус бесконечность) и
 (плюс бесконечность), считая по определению,
что:
(плюс бесконечность), считая по определению,
что:
 .
.
Множество
действительных чисел, дополненное
элементами
и
будем называть расширенным множеством
действительных чисел и обозначать
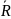 .
Определим некоторые важные типы
подмножеств
.
Пусть
.
Определим некоторые важные типы
подмножеств
.
Пусть

 :
:
1)
Отрезок:
 ;
;
2)
Интервал:
 ;
;
3)
Полуинтервал:
 или
или
 .
.
